Содержание
- 2. План. 1 Приращение аргумента. Приращение функции. 2. Определения производной. 3. Вычисление производных. 4. Правила дифференцирования. 5.
- 3. Опр. 1. Пусть ф-я определена в точках х0 и х1. Разность х1-х0 называют приращением аргумента (при
- 4. Пример 1. Найти приращение функции у=х2 при переходе от точки х0=1 к точке: Обратите внимание на
- 5. Пример 2. Для функции у=х2 найти:
- 6. 2. Определения производной. Опр. 2. Пусть функция определена в точке х и в некоторой точке ее
- 7. Если функция имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру отыскания
- 8. 3. Вычисление производных. Таблица производных
- 9. Правила дифференцирования. Правило 1. Если функция и имеют производную в точке х, то и их сумма
- 10. Правило 3. Если функция и имеют производную в точке х, то и их произведение имеет производную
- 18. Скачать презентацию












 Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Определение и знаки тригонометрических функций
Определение и знаки тригонометрических функций Математическая статистика
Математическая статистика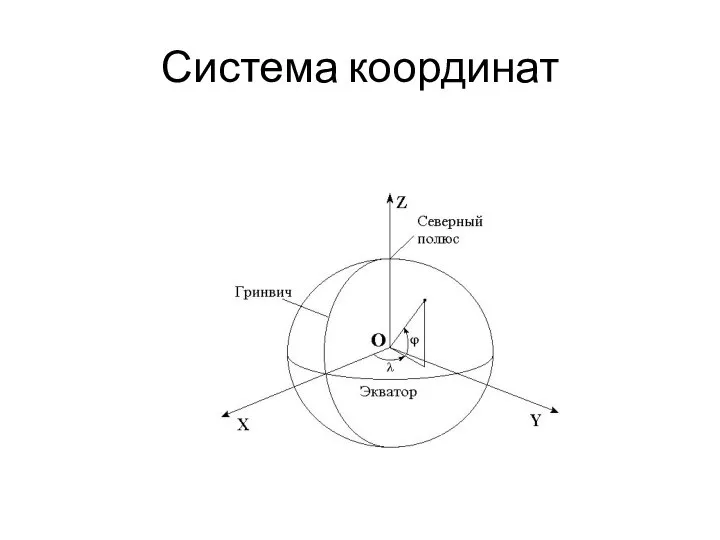 Система координат. Географические координаты
Система координат. Географические координаты Смешанные дроби. 5 класс
Смешанные дроби. 5 класс Построение сечений
Построение сечений Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной Таблица умножения на 2
Таблица умножения на 2 Ряды. Действия над рядами
Ряды. Действия над рядами Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Презентация на тему Решение неравенств методом интервалов
Презентация на тему Решение неравенств методом интервалов  Тема 6_2022
Тема 6_2022 Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Контрольная работа. Логарифм, логарифмическая функция
Контрольная работа. Логарифм, логарифмическая функция Равенство и неравенство. (1 класс)
Равенство и неравенство. (1 класс) Диаграмма - понятие, типы, основы и особенности составления
Диаграмма - понятие, типы, основы и особенности составления Сложение двузначных чисел
Сложение двузначных чисел Абсолютная и относительная погрешность округления чисел
Абсолютная и относительная погрешность округления чисел Сравнение многозначных чисел. 4 класс
Сравнение многозначных чисел. 4 класс Математический анализ
Математический анализ Умножение вектора на число
Умножение вектора на число Элементы векторной алгебры
Элементы векторной алгебры Симметрия вокруг нас
Симметрия вокруг нас Русский крестьянский способ умножения
Русский крестьянский способ умножения Путешествие в страну Геометрию
Путешествие в страну Геометрию Векторы. Задания
Векторы. Задания Презентация на тему Геометрические построения с помощью циркуля и линейки
Презентация на тему Геометрические построения с помощью циркуля и линейки