Площадь поверхности призмы

Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.
Галилео Галилей.

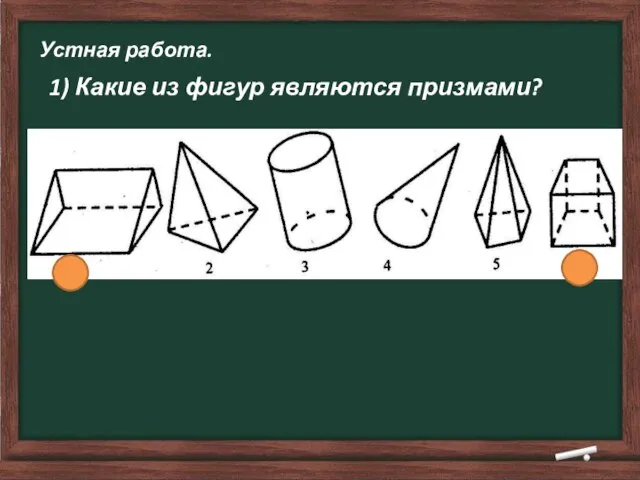
Устная работа.
1) Какие из фигур являются призмами?

2) Обозначьте и назовите для призмы: (изобразить призму на доске)
вершины
основания
боковые грани
противоположные грани
диагонали грани
диагонали призмы

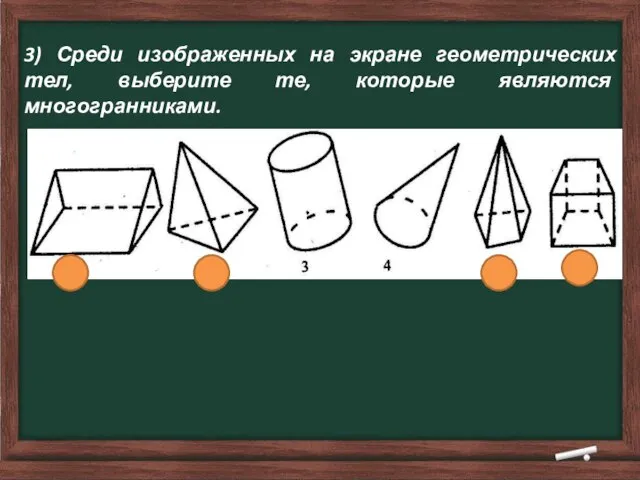
3) Среди изображенных на экране геометрических тел, выберите те, которые являются многогранниками.

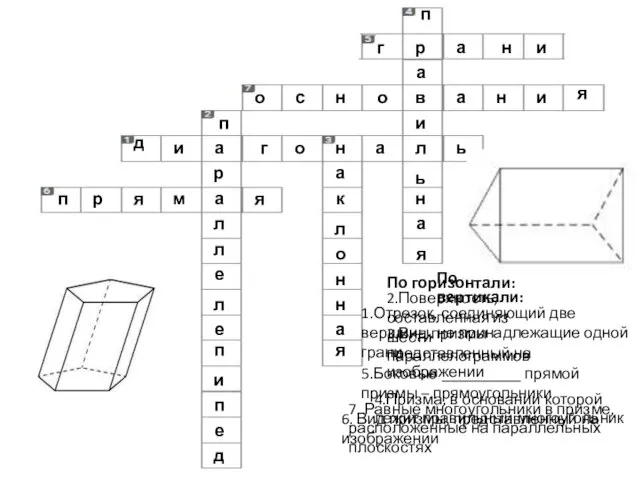
По горизонтали:
1.Отрезок, соединяющий две вершины, не принадлежащие одной грани
д
и
а
г
о
н
а
л
ь
5.Боковые __________ прямой призмы – прямоугольники
г
р
а
н
и
6. Вид призмы, представленный на изображении
п
р
я
м
а
я
7. Равные многоугольники в призме, расположенные на параллельных плоскостях
о
с
н
о
в
а
н
и
я
По вертикали:
2.Поверхность, составленная из шести параллелограммов
п
р
л
л
е
л
е
п
и
п
е
д
3.Вид призмы представленный на изображении
а
к
л
о
н
н
а
я
4.Призма, в основании которой лежит правильный многоугольник
п
а
и
ь
н
а
я

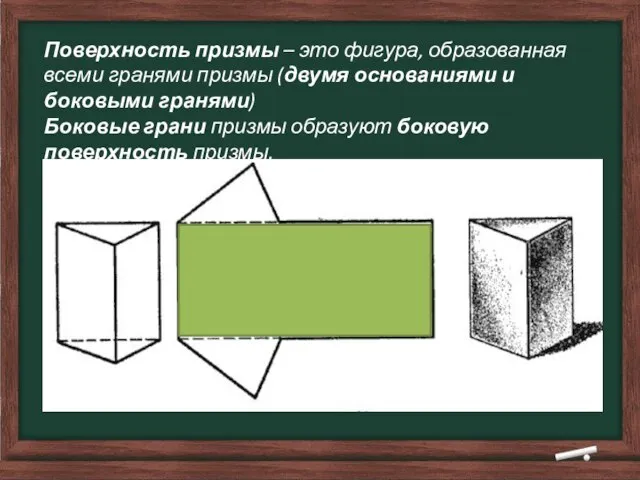
Поверхность призмы – это фигура, образованная всеми гранями призмы (двумя основаниями и боковыми гранями)
Боковые грани призмы образуют боковую поверхность призмы.

Площадью полной поверхности призмы на­зывается сумма площадей всех ее граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней. Площадь Sполн полной поверхности выражается через площадь боковой поверхности и площадь основания призмы формулой
Sполн = Sбок + 2Sосн

Теорема
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Sбок(прям. пр.) = Pосн.h.

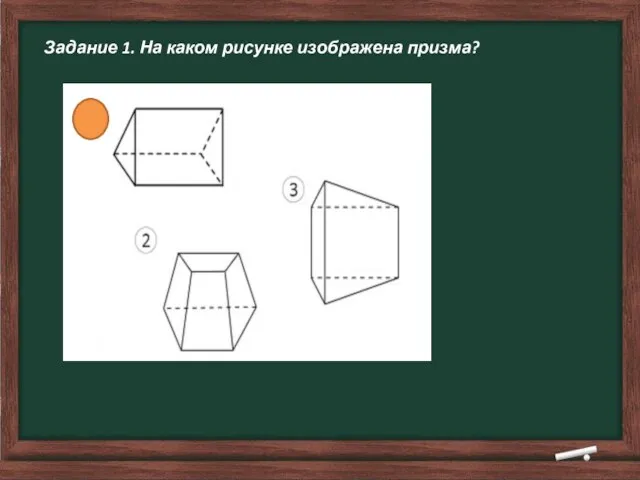
Задание 1. На каком рисунке изображена призма?

Задание 2.
Сторона основания правильной четырехугольной призмы равна 5. Высота призмы равна 10. Чему равна...
площадь основания?
площадь боковой поверхности?
площадь полной поверхности?
25
200
250