Краткая история появления и развития пределов

Определение предела
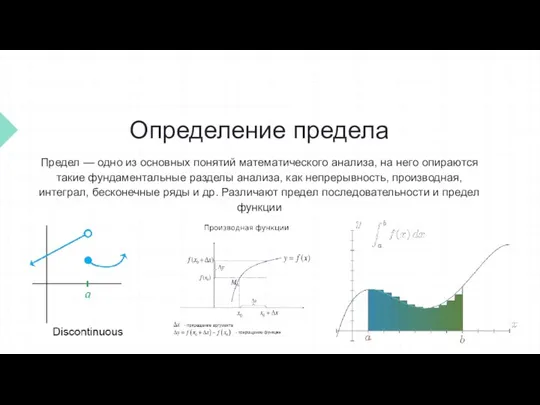
Предел — одно из основных понятий математического анализа, на него опираются такие фундаментальные разделы анализа, как непрерывность, производная, интеграл, бесконечные ряды и др. Различают предел последовательности и предел функции

История обоснования термина "Предел"
Интуитивное понятие о предельном переходе использовалось ещё учеными Древней Греции при вычислении площадей и объёмов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.
При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.
Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.
С помощью теории пределов в первой половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций

История символа lim
Общепринятый символ предела был предложен Симоном Люилье (1787 год) в следующем формате: это обозначение получило поддержку Коши (1821). Точка после lim вскоре исчезла. Близкое к современному обозначение предела ввёл Вейерштрасс, хотя вместо привычной нам стрелки он использовал знак равенства:
Стрелка появилась в начале XX века сразу у нескольких математиков. Обозначения для одностороннего предела вида: первым предложил Дирихле (1837) в
виде: Мориц Паш (1887) ввёл другие важные понятия — верхнего и нижнего предела, которые записывал в виде: и соответственно. За рубежом эта символика стала стандартной, а в отечественной литературе преобладают другие обозначения: введенные Альфредом Прингсхаймом в 1898 году.