Содержание
- 2. Комбинационная схема состоит из логических элементов и реализует булеву функцию или совокупность булевых функций. Под логическим
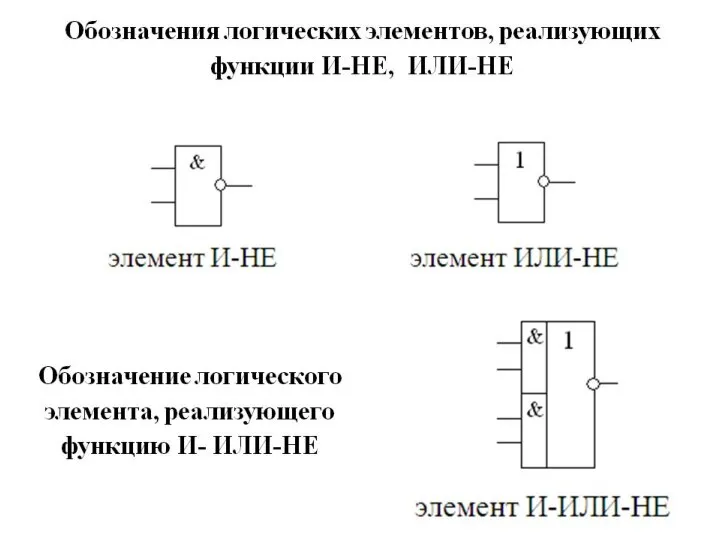
- 3. Базис (совокупность) элементов, выбранных для синтеза КС, всегда должны быть функционально полным, то есть допускать реализацию
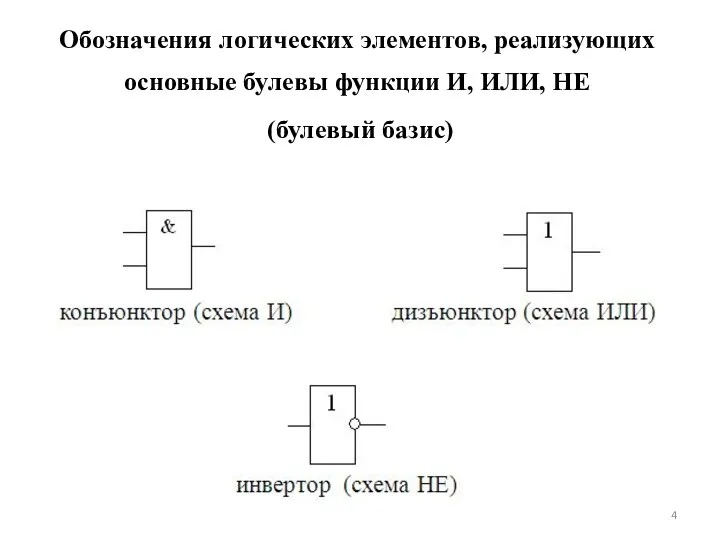
- 4. Обозначения логических элементов, реализующих основные булевы функции И, ИЛИ, НЕ (булевый базис)
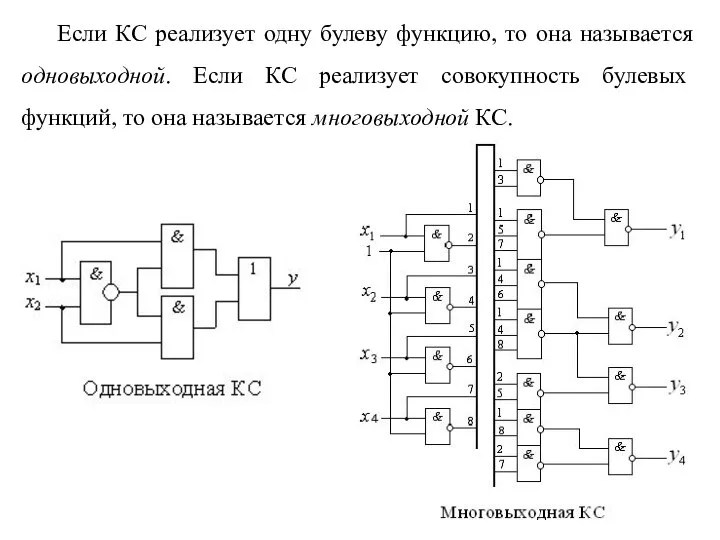
- 6. Если КС реализует одну булеву функцию, то она называется одновыходной. Если КС реализует совокупность булевых функций,
- 7. Задача анализа заданной КС сводится к отысканию булевой функции или системы булевых функций, описывающих работу этой
- 8. Задача синтеза КС состоит в построении оптимальной схемы проектируемого узла устройства, исходя из физического описания его
- 9. Основные критерии качества технической реализации КС: Сложность оборудования. На практике оцениваются числом корпусов ИМС, используемых в
- 10. СИНТЕЗ ОДНОВЫХОДНЫХ КОМБИНАЦИОННЫХ СХЕМ Задача синтеза схемы состоит в преобразовании логических функций в суперпозицию логических элементов
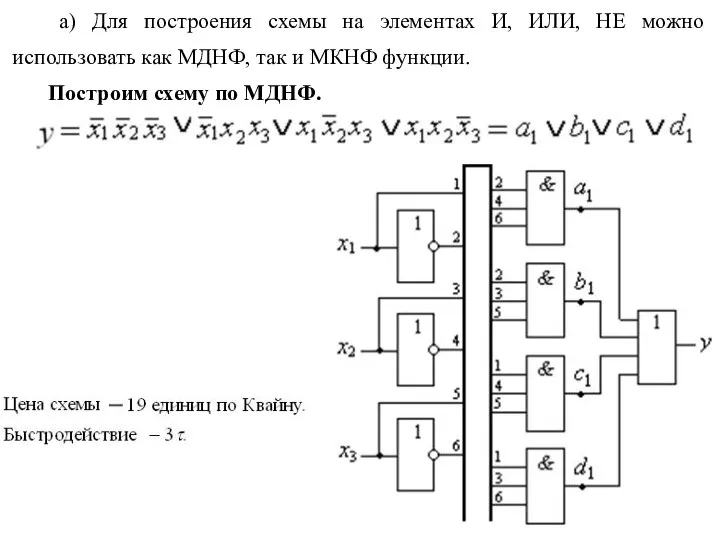
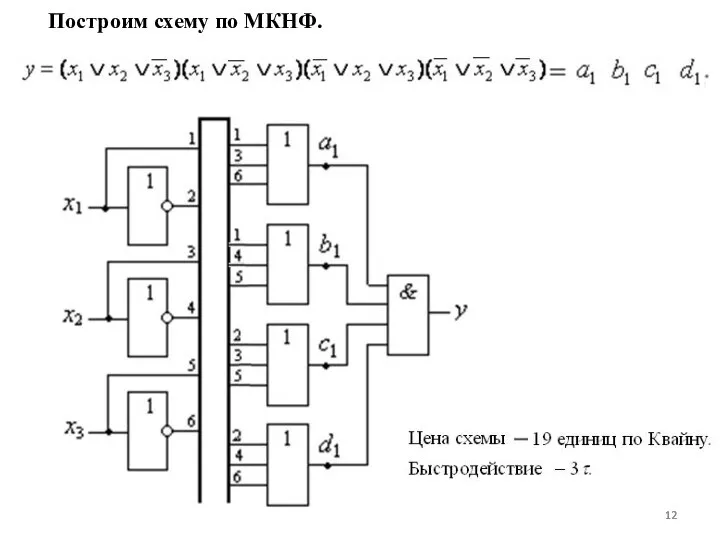
- 11. а) Для построения схемы на элементах И, ИЛИ, НЕ можно использовать как МДНФ, так и МКНФ
- 12. Построим схему по МКНФ.
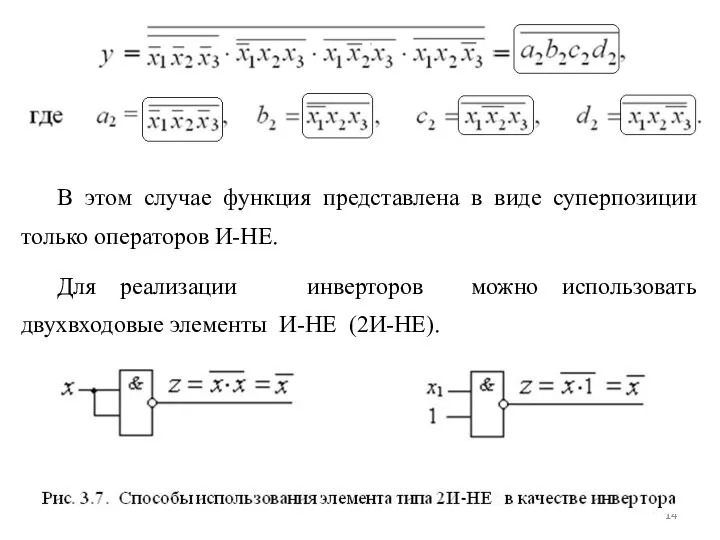
- 13. б) Для реализации исходной булевой функции на элементах И-НЕ необходимо от МДНФ функции взять двойное отрицание
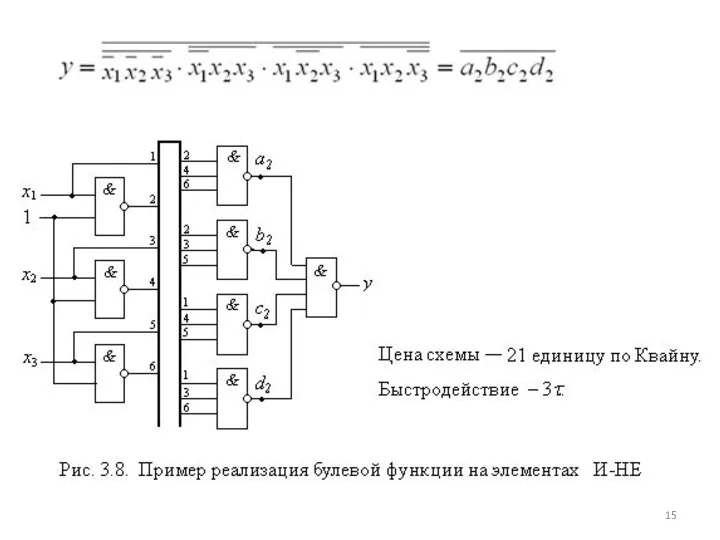
- 14. В этом случае функция представлена в виде суперпозиции только операторов И-НЕ. Для реализации инверторов можно использовать
- 16. в) Для реализации исходной булевой функции на элементах ИЛИ-НЕ необходимо от МКНФ функции взять двойное отрицание
- 17. В этом случае функция представлена в виде суперпозиции только операторов ИЛИ-НЕ. Для реализации инверторов можно использовать
- 19. Скачать презентацию









 Средняя линия треугольника
Средняя линия треугольника Задачи на нахождение площади треугольника
Задачи на нахождение площади треугольника Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора Параллельность плоскостей
Параллельность плоскостей Сумма углов в треугольнике
Сумма углов в треугольнике Раздел 3. Линейная алгебра с элементами аналитической геометрии
Раздел 3. Линейная алгебра с элементами аналитической геометрии Дидактическая игра. Какого фрагмента не хватает на картинке (для дошкольников)
Дидактическая игра. Какого фрагмента не хватает на картинке (для дошкольников) Правильная пирамида
Правильная пирамида Вычитаем числа
Вычитаем числа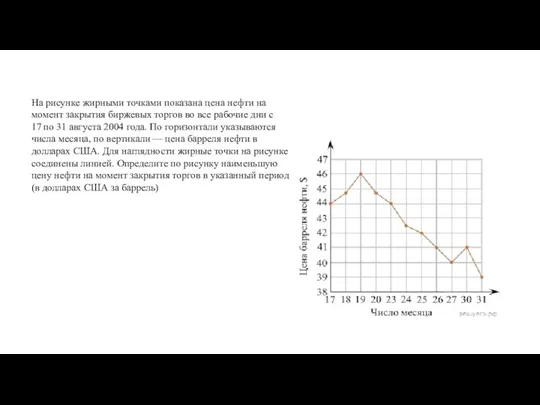 Вариант 1
Вариант 1 Двугранные углы
Двугранные углы Треугольники
Треугольники Решение задач с помощью уравнений
Решение задач с помощью уравнений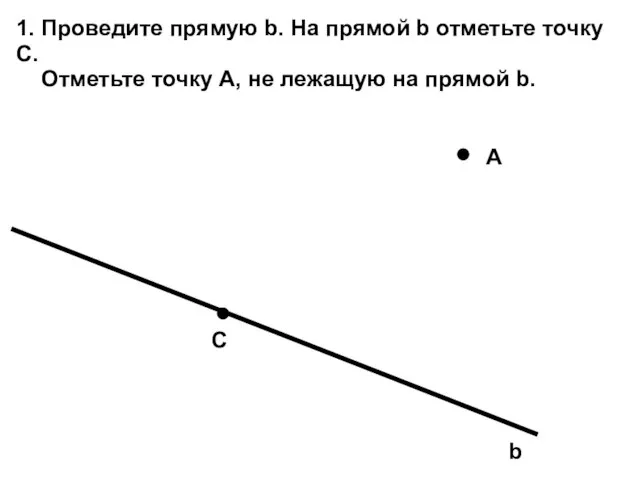 Пересекающиеся и параллельные прямые
Пересекающиеся и параллельные прямые Презентация на тему Сложение и вычитание дробей с разными знаменателями
Презентация на тему Сложение и вычитание дробей с разными знаменателями  Прямая, кривая, ломаная
Прямая, кривая, ломаная Основы векторного исчисления
Основы векторного исчисления Проценты чисел
Проценты чисел Векторы
Векторы Используется ли в учебниках 7-го класса термин Функциональная зависимость?
Используется ли в учебниках 7-го класса термин Функциональная зависимость? Решение задач. 1 класс
Решение задач. 1 класс Прямая. Тест
Прямая. Тест Уравнение с двумя переменными
Уравнение с двумя переменными Математическое моделирование. Воспроизводимость опытов
Математическое моделирование. Воспроизводимость опытов Вікористання спадщини видатних математиків Полтавщини на уроках математики
Вікористання спадщини видатних математиків Полтавщини на уроках математики Теорема Пифагора
Теорема Пифагора Презентация на тему ГИА 2013. Модуль Геометрия №10
Презентация на тему ГИА 2013. Модуль Геометрия №10  Объем. Цилиндр, призма
Объем. Цилиндр, призма