Содержание
- 2. Задачи определения оценок параметров выборки Рассмотрим простейшие задачи данного типа.
- 3. При анализе результатов исследований полезно иметь представление о разбросе данных в числовом ряду. Размах ряда один
- 4. Рассмотрим наиболее часто используемый на практике статистический показатель – дисперсия. Представлен ряд чисел 4; 8; 12;
- 5. Вычислим отклонение каждого члена ряда от среднего арифметического: 4 – 10 = –6; 8 – 10
- 6. Данный показатель не может характеризировать разброс данных, так как для любого ряда чисел он всегда будет
- 7. Дисперсией ряда чисел называется среднее арифметическое квадратов их отклонений от среднего арифметического этого ряда. Дисперсия –
- 8. Рассмотрим пример. Кто лучше готов к соревнованиям? Спортсмены проводили подготовку к соревнованиям по стрельбе из лука.
- 9. Найдём среднее арифметическое для каждого спортсмена. Значения одинаковы.
- 10. Вычислим дисперсию результатов для каждого спортсмена.
- 11. Обратите внимание на полученные значения. Разброс данных у первого спортсмена меньше (0,86 Данный пример демонстрирует, что
- 12. Если в ряду содержится большое число данных, среди которых есть лишь несколько данных, значительно отличающихся от
- 13. Недостаток дисперсии. Если исследуемые величины измеряются в каких-либо линейных единицах измерения: килограммах, метрах, часах и т.
- 15. Скачать презентацию












 Медианы, биссектрисы и высоты треугольника. 7 класс
Медианы, биссектрисы и высоты треугольника. 7 класс Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Фракталы в литературе
Фракталы в литературе Математическая викторина. 6 – 7 классы
Математическая викторина. 6 – 7 классы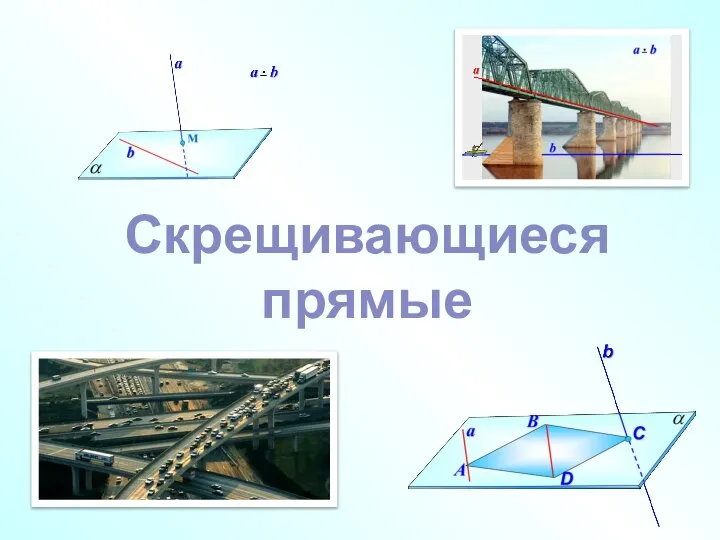 Скрещивающиеся прямые
Скрещивающиеся прямые Вписанная окружность
Вписанная окружность Проект Колодец. Деловая игра по теме Цилиндр
Проект Колодец. Деловая игра по теме Цилиндр Подобные слагаемые
Подобные слагаемые Презентация на тему Натуральные логарифмы
Презентация на тему Натуральные логарифмы  Определение и свойства тройных интегралов
Определение и свойства тройных интегралов Обобщающий урок по теме Многогранники
Обобщающий урок по теме Многогранники Письменное деление на трёхзначное число
Письменное деление на трёхзначное число Построение треугольников по трем элементам
Построение треугольников по трем элементам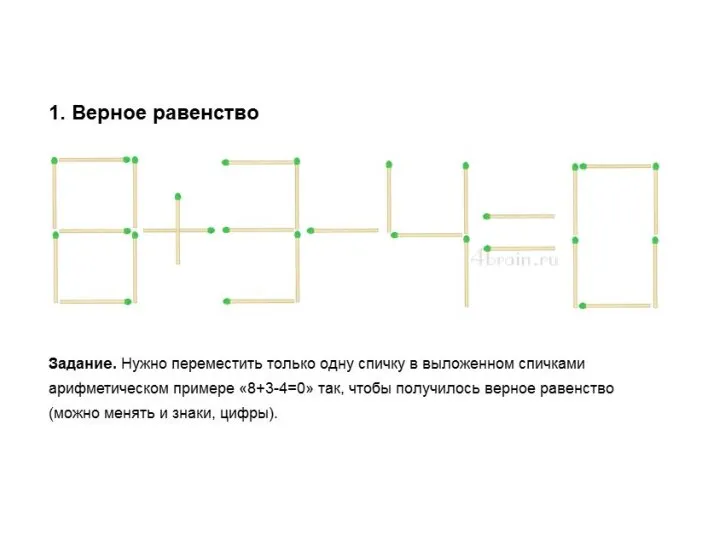 Спички
Спички Операции над множествами
Операции над множествами Натуральные числа. Викторина
Натуральные числа. Викторина Презентация на тему Прямоугольный параллелепипед. Куб
Презентация на тему Прямоугольный параллелепипед. Куб  Что узнали? Чему научились?
Что узнали? Чему научились? Двоичная арифметика
Двоичная арифметика Тригонометриялық функциялардың қос бұрышының және жарты бұрышының формулалары
Тригонометриялық функциялардың қос бұрышының және жарты бұрышының формулалары О сохранении и нарушении равносильности при решении уравнений и неравенств
О сохранении и нарушении равносильности при решении уравнений и неравенств Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Декартова система координат в евклидовом пространстве
Декартова система координат в евклидовом пространстве Ряды распределения. Практическое занятие 4
Ряды распределения. Практическое занятие 4 Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Измерение углов без транспортира
Измерение углов без транспортира Кут. Вимірювання кутів. Рівність кутів. Бісектриса кута
Кут. Вимірювання кутів. Рівність кутів. Бісектриса кута Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -