Первообразная функция

Функцию y = F(x) называют первообразной для функции y = f (x) на заданном промежутке X, если для любого x ϵ X выполняется равенство
Fˈ(x)= f (x)
Определение первообразной

Определите от какой функции взята производная:
Функция
Первообразная
C

Определите от какой функции
взята производная:
Функция
Первообразная
-

Определите от какой функции
взята производная:
Функция
Первообразная

Определите от какой функции
взята производная:
Функция
Первообразная

Найдите первообразную функции:
От каких функций взяли производные и получили данные функции?

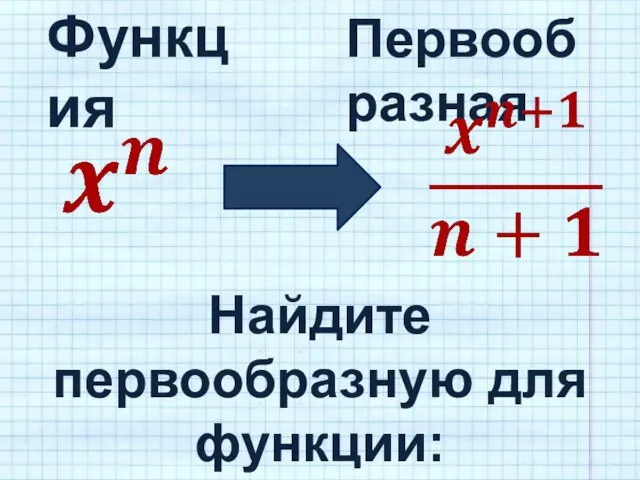
Функция
Первообразная
Найдите первообразную для функции:

Процесс отыскания производной по заданной функции называют
дифференцированием
Процесс отыскания функции по заданной производной (нахождение первообразной) называют
интегрированием

Всякая функция имеет бесконечное множество первообразных
Если функция F (x) является первообразной функции f (x) на некотором промежутке, то все первообразные функции f ˈ(x) записываются в виде F (x) + C, где С – произвольная постоянная

Определите, является ли функция F (x) первообразной функции f (x):
Решение:
Fˈ(x) = 6x-4 Fˈ(x) = f(x)
Ответ: да, является

Определите, является ли функция F (x) первообразной функции f (x):

Правило отыскания первообразных
Правило 1
Первообразная суммы равна сумме первообразных
Если функция y=f (x) и y=g(x) имеют на промежутке X первообразные соответственно y=F(x) и y=G(x), то сумма функций y=f(x)+g(x) имеют на промежутке Х первообразную, причём одной из них является функция y=F(x)+G(x)

Найдите первообразную функции

Правило отыскания первообразных
Правило 2
Если F(x) – первообразная для f (x), то R F(x) – первообразная для R f (x)