Содержание
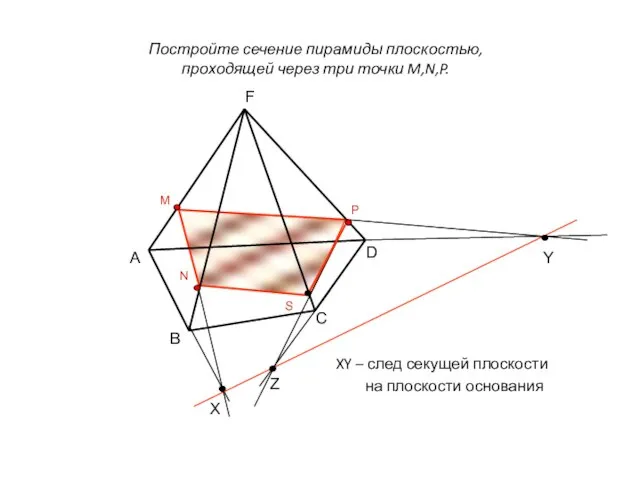
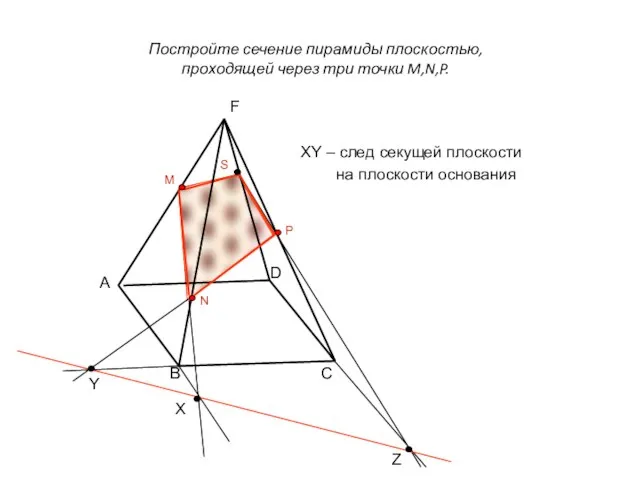
- 2. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P. XY – след секущей плоскости на плоскости
- 3. XY – след секущей плоскости на плоскости основания D C B Z Y X M N
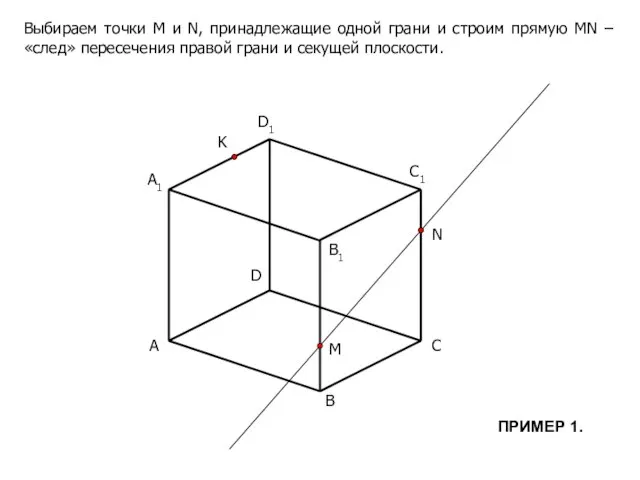
- 4. A B C D B1 C1 D1 M N K Выбираем точки М и N, принадлежащие
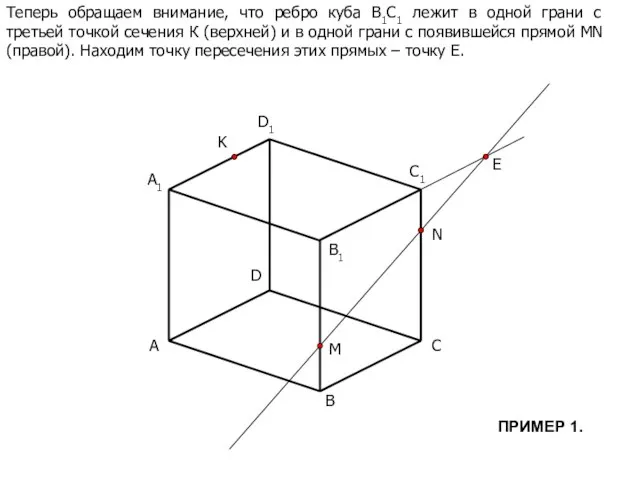
- 5. A B C D B1 C1 D1 M N K A1 E Теперь обращаем внимание, что
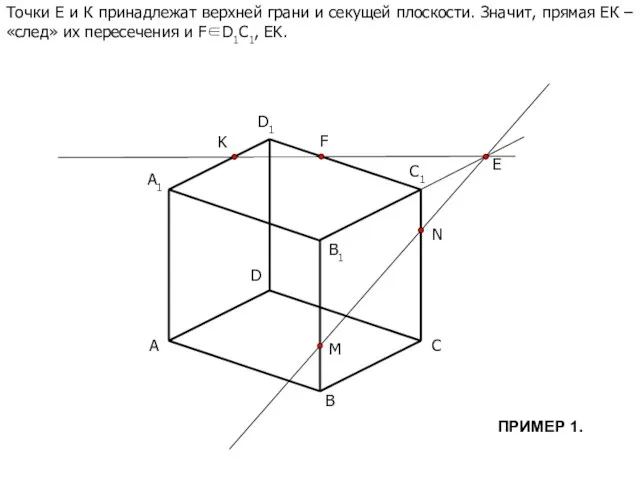
- 6. A B C D B1 C1 D1 M N K A1 E Точки Е и К
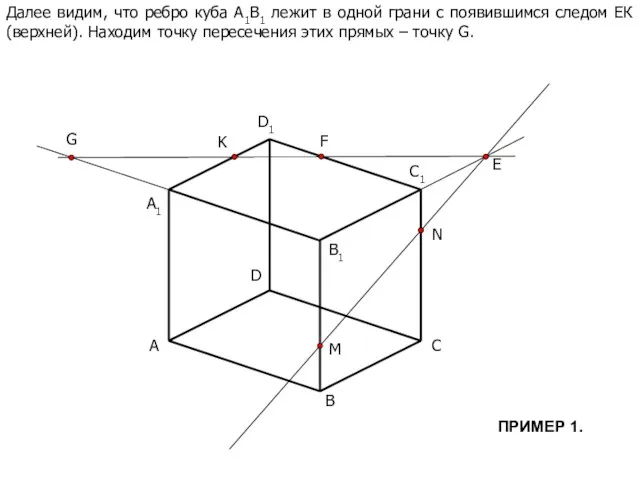
- 7. A B C D B1 C1 D1 M N K A1 E F Далее видим, что
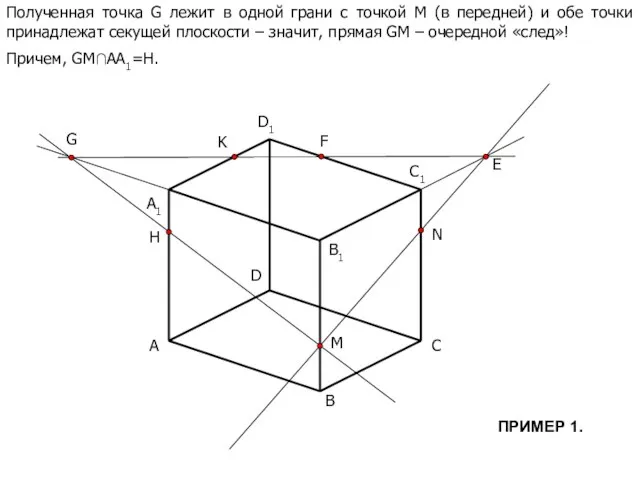
- 8. A B C D B1 C1 D1 M N K A1 E F G Полученная точка
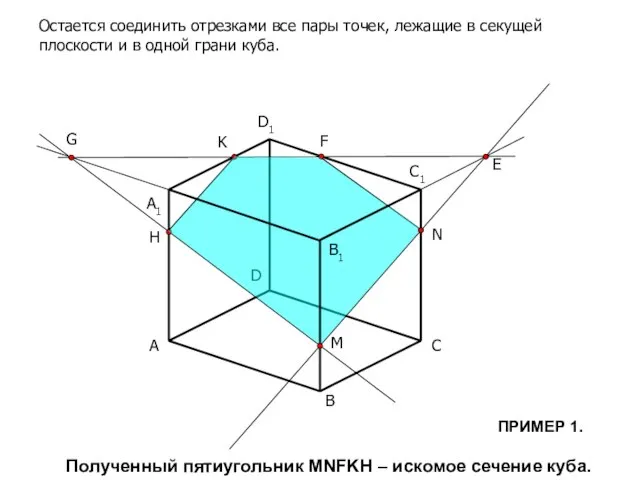
- 9. A B C D C1 D1 M N K A1 E F G H Остается соединить
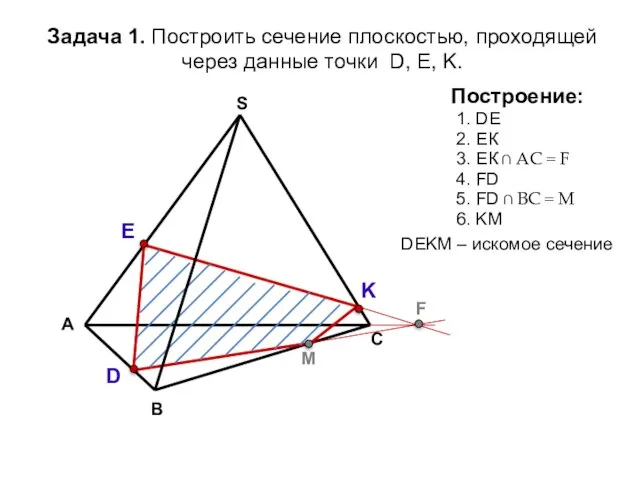
- 10. А В С S Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
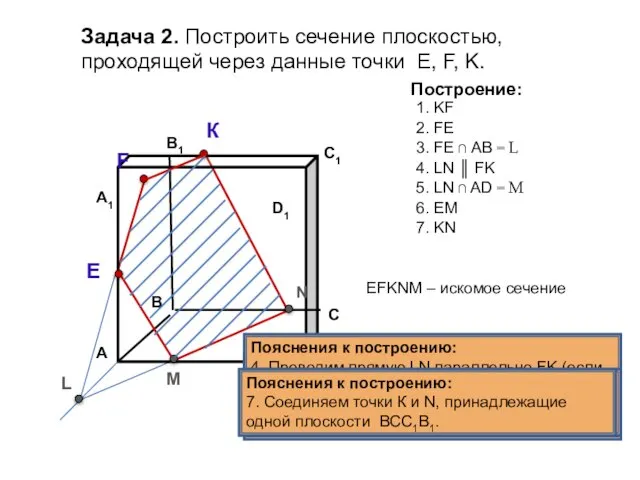
- 11. Пояснения к построению: 1. Соединяем точки K и F, принадлежащие одной плоскости А1В1С1D1. Задача 2. Построить
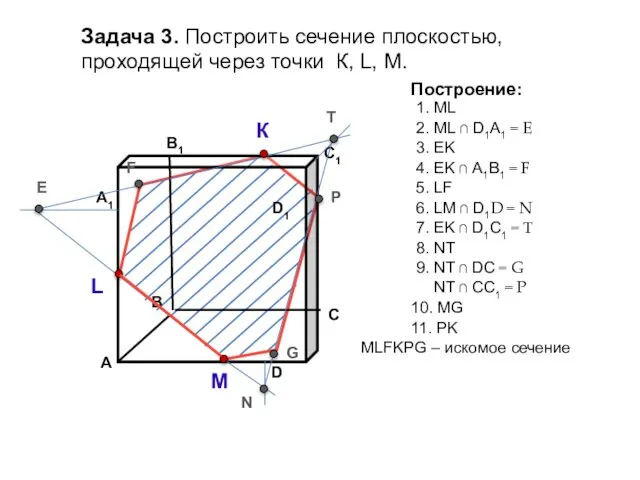
- 12. Задача 3. Построить сечение плоскостью, проходящей через точки К, L, М. К L М Построение: 1.
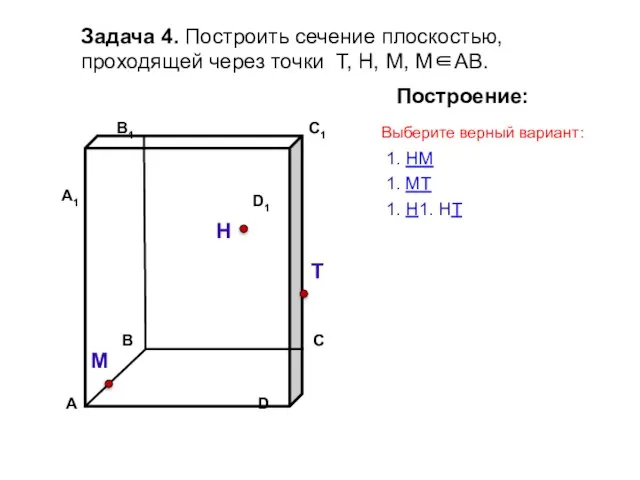
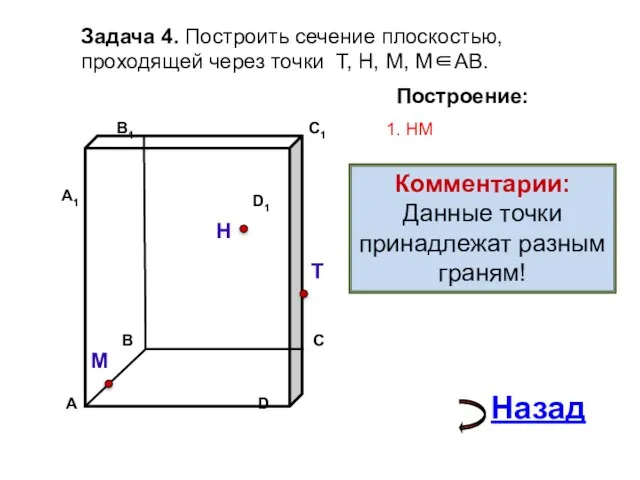
- 13. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
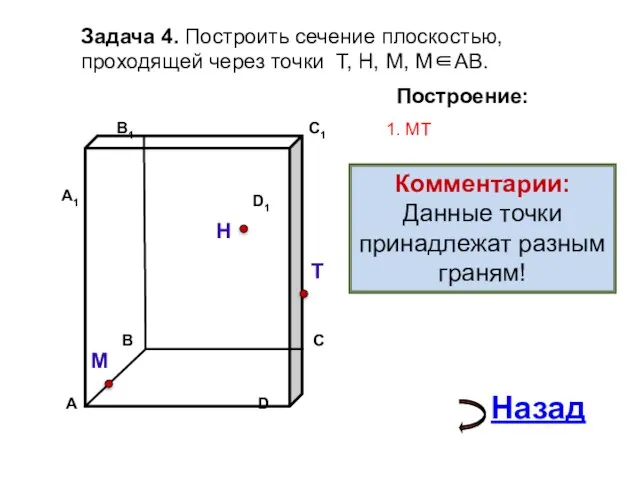
- 14. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
- 15. Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ. Н Т М Построение:
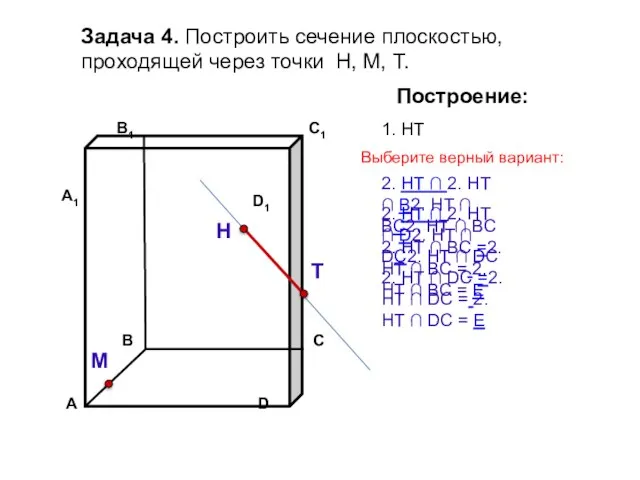
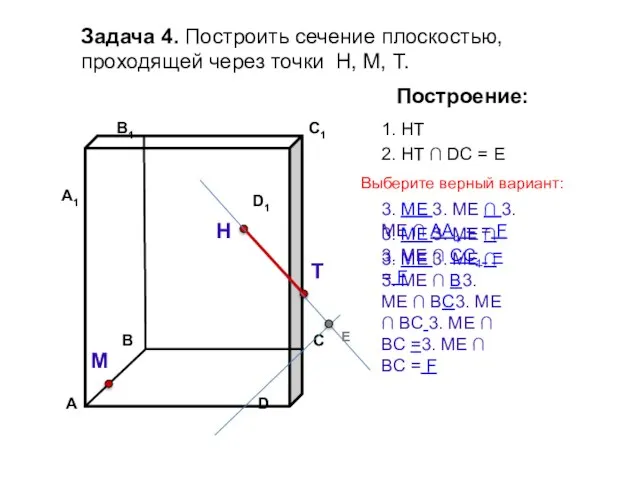
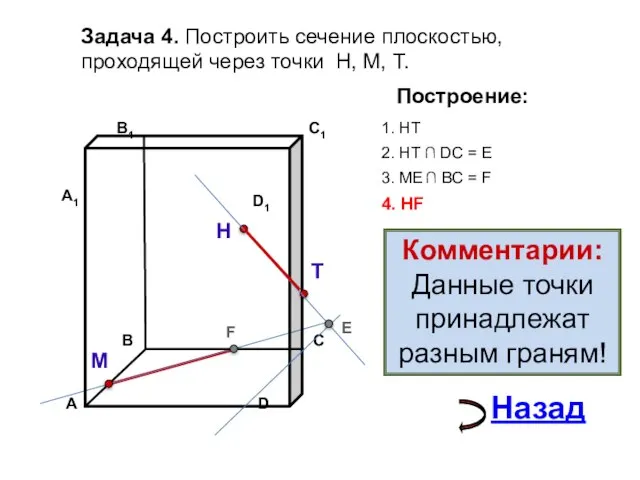
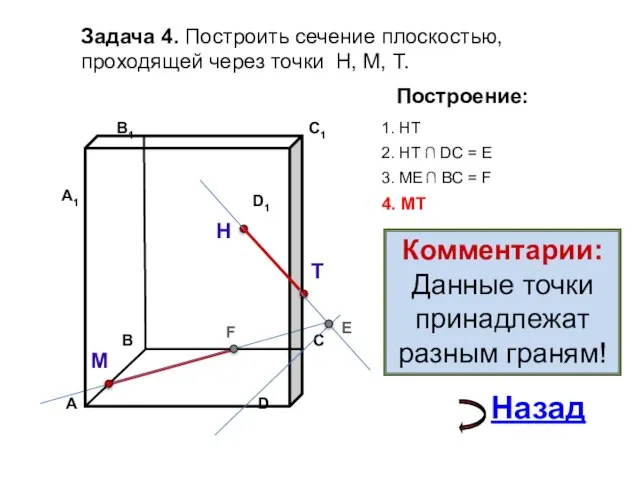
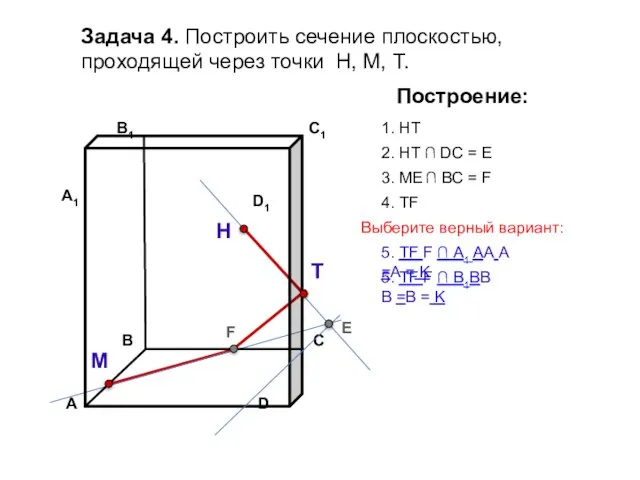
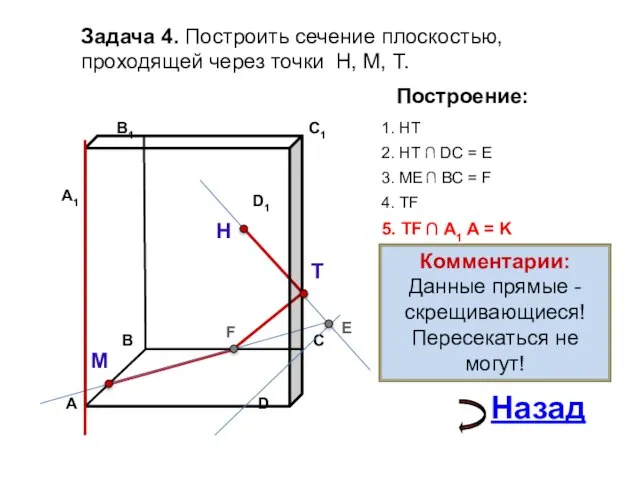
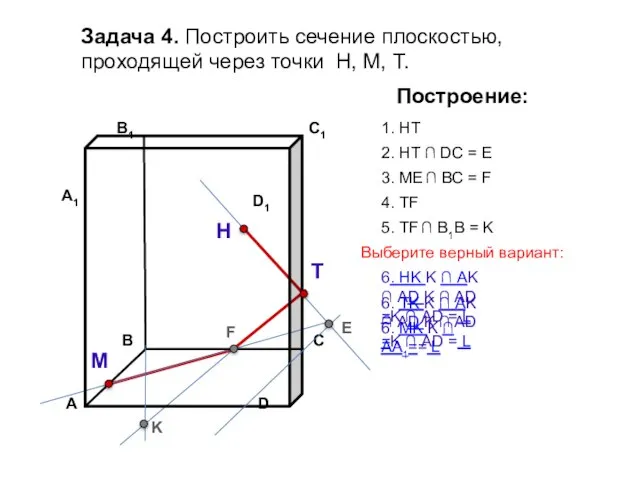
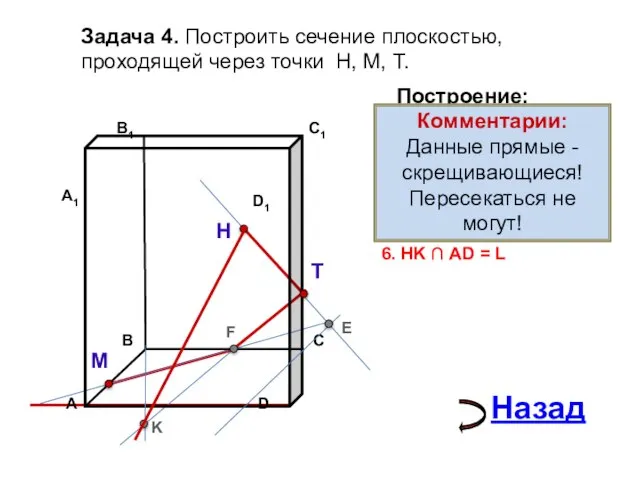
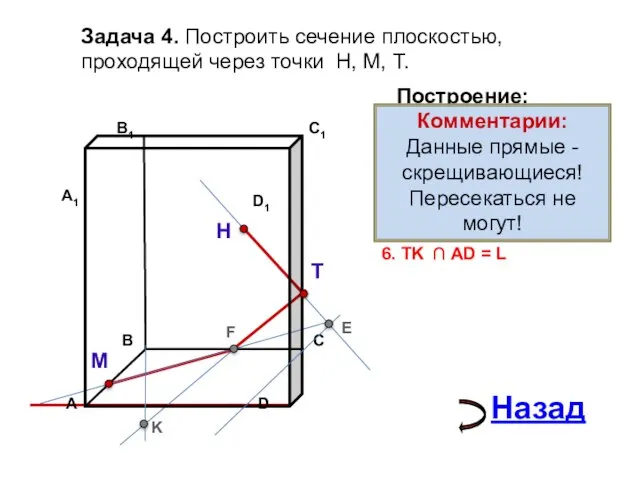
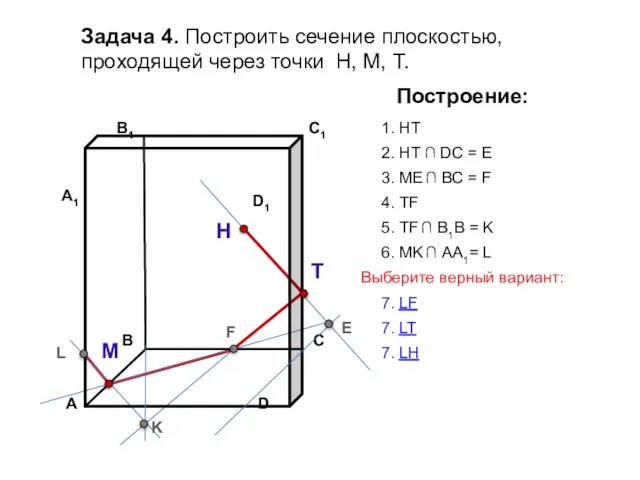
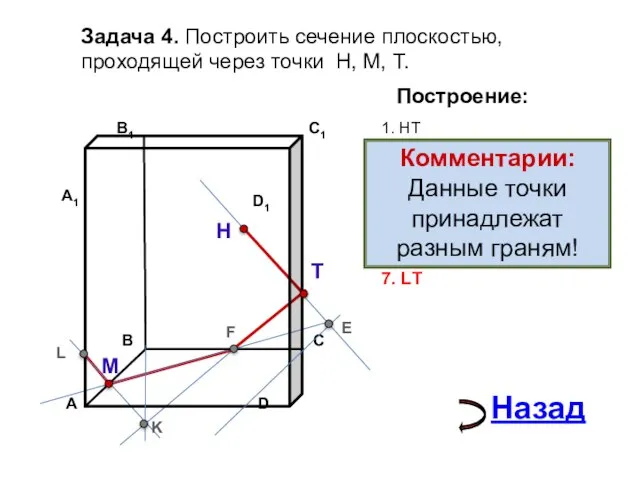
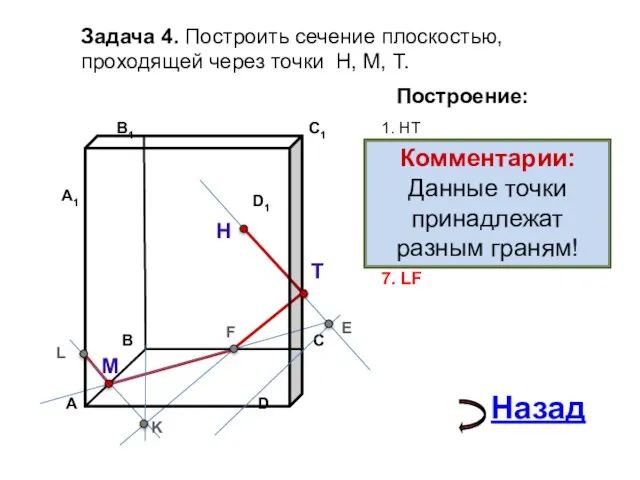
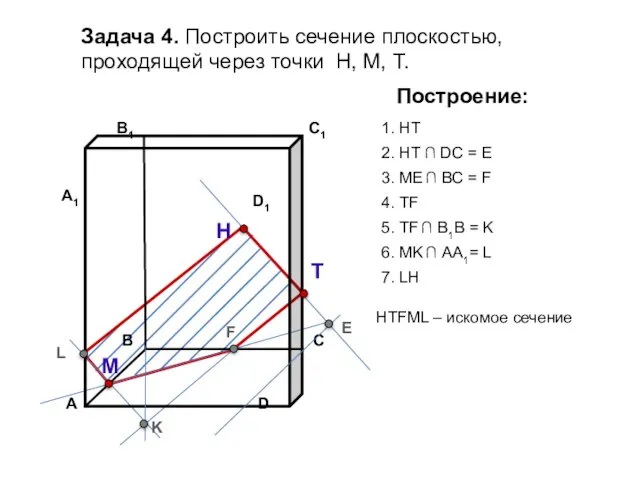
- 16. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
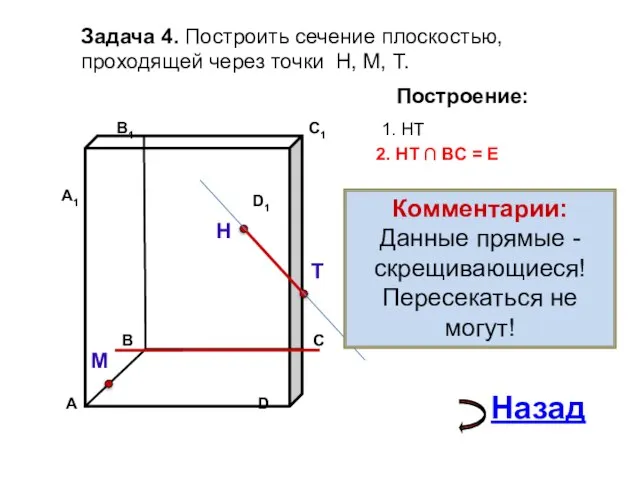
- 17. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 18. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 19. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
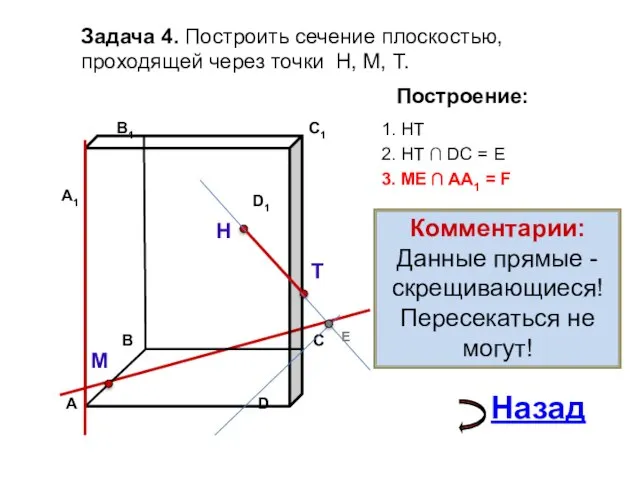
- 20. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 21. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
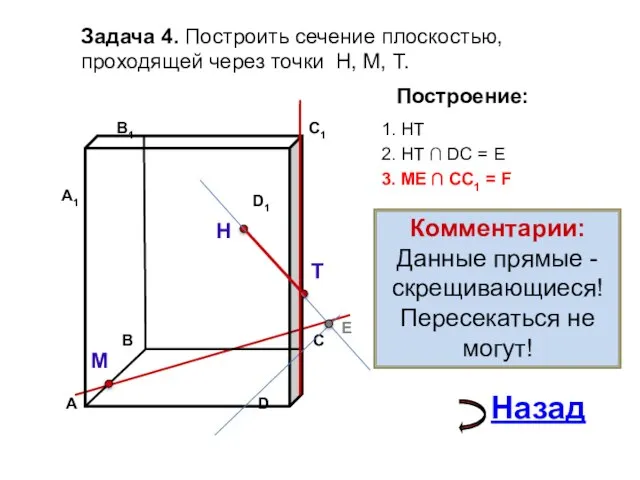
- 22. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 23. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
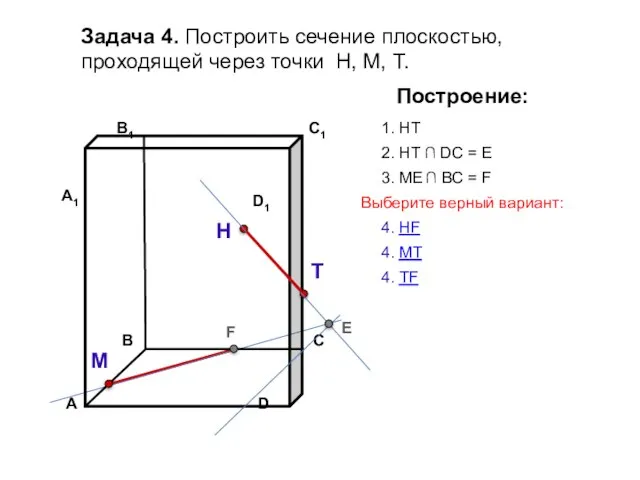
- 24. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 25. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 26. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 27. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 28. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 29. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 30. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 31. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
- 32. Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т. Н Т М Построение: 1.
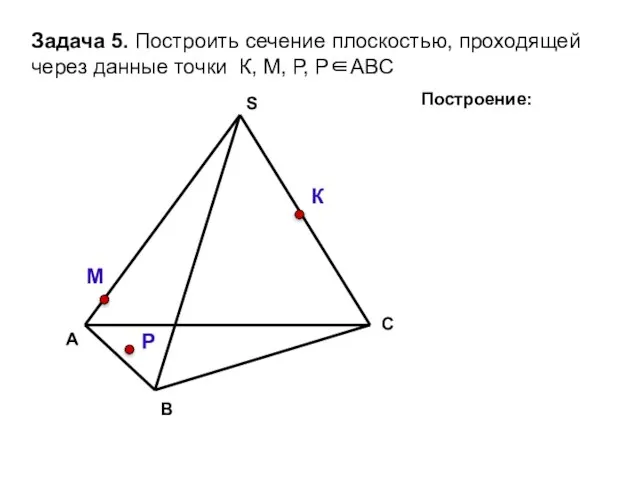
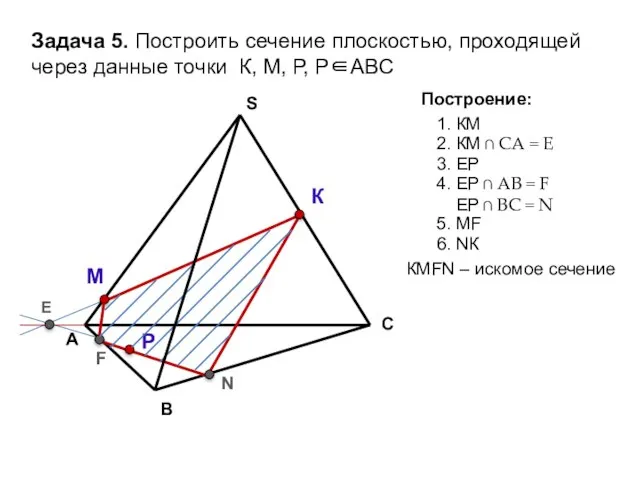
- 33. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 34. А В С S Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р,
- 36. Скачать презентацию
 Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции
Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции Уравнения. Графики
Уравнения. Графики Математические шифровки
Математические шифровки Сумма углов треугольника
Сумма углов треугольника Решение задач на разностное сравнение 2 класс - Презентация
Решение задач на разностное сравнение 2 класс - Презентация Восстанови ряд чисел
Восстанови ряд чисел Рівнобедрений трикутник і його властивості
Рівнобедрений трикутник і його властивості Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2
Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2 Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика
Теория вероятностей. Лекция 1: Основные понятия теории вероятностей. Комбинаторика Презентация на тему Перпендикулярность прямой и плоскости
Презентация на тему Перпендикулярность прямой и плоскости  Проценты
Проценты Линейные рекуррентные соотношения и методы их решения
Линейные рекуррентные соотношения и методы их решения Пропорция
Пропорция Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Презентация на тему Вычисления с многозначными числами
Презентация на тему Вычисления с многозначными числами  Логарифмическая функция
Логарифмическая функция История математики. Брейн-ринг, 10 класс
История математики. Брейн-ринг, 10 класс 70 задач на чертежах по планиметрии
70 задач на чертежах по планиметрии Матрицы и действия над ними
Матрицы и действия над ними Понятие цилиндра
Понятие цилиндра Презентация по математике "Основы концепции “глубинного анализа текстов" -
Презентация по математике "Основы концепции “глубинного анализа текстов" -  дз
дз Статистика
Статистика Соседи числа
Соседи числа Единицы измерения. Килограмм. Грамм
Единицы измерения. Килограмм. Грамм Возведение в степень произведения. 7 класс
Возведение в степень произведения. 7 класс Числа и их свойства. Числовые множества. Признаки делимости
Числа и их свойства. Числовые множества. Признаки делимости Математика и здоровье
Математика и здоровье