Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4

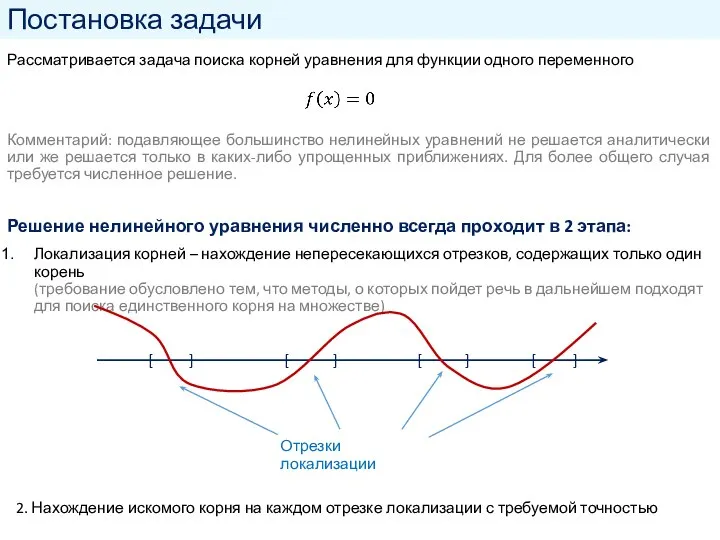
Постановка задачи
Рассматривается задача поиска корней уравнения для функции одного переменного
Комментарий: подавляющее большинство нелинейных уравнений не решается аналитически или же решается только в каких-либо упрощенных приближениях. Для более общего случая требуется численное решение.
Решение нелинейного уравнения численно всегда проходит в 2 этапа:
Локализация корней – нахождение непересекающихся отрезков, содержащих только один корень
(требование обусловлено тем, что методы, о которых пойдет речь в дальнейшем подходят для поиска единственного корня на множестве)
2. Нахождение искомого корня на каждом отрезке локализации с требуемой точностью
[ ] [ ] [ ] [ ]
Отрезки локализации

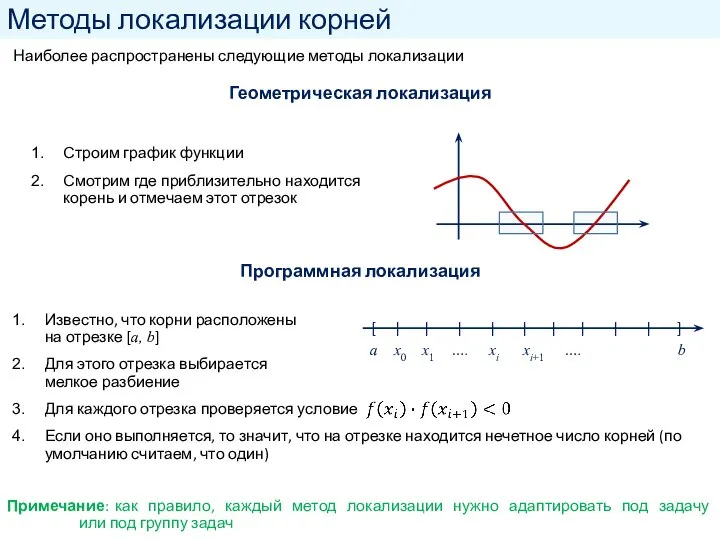
Методы локализации корней
Строим график функции
Смотрим где приблизительно находится корень и отмечаем этот отрезок
Геометрическая локализация
Наиболее распространены следующие методы локализации
Программная локализация
Известно, что корни расположены
на отрезке [a, b]
Для этого отрезка выбирается
мелкое разбиение
Для каждого отрезка проверяется условие
Если оно выполняется, то значит, что на отрезке находится нечетное число корней (по умолчанию считаем, что один)
[ | | | | | | | | | ]
a x0 x1 …. xi xi+1 …. b
Примечание: как правило, каждый метод локализации нужно адаптировать под задачу
или под группу задач

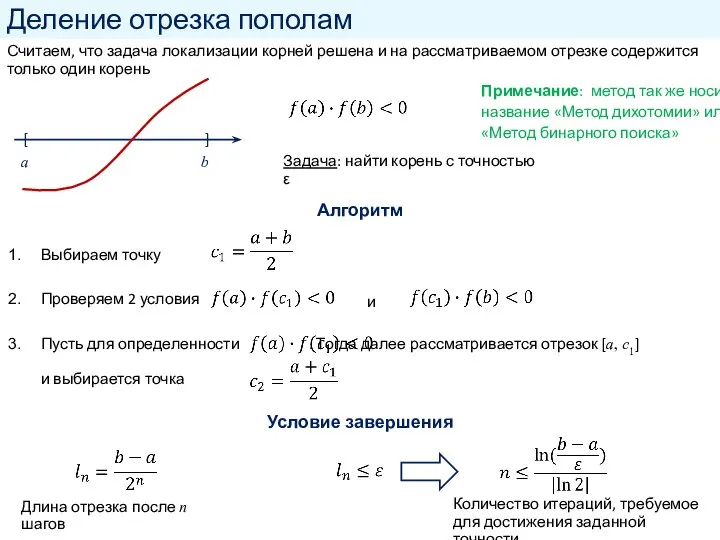
Деление отрезка пополам
Считаем, что задача локализации корней решена и на рассматриваемом отрезке содержится только один корень
Задача: найти корень с точностью ε
[ ]
a b
Примечание: метод так же носит название «Метод дихотомии» или «Метод бинарного поиска»
Выбираем точку
Проверяем 2 условия
Пусть для определенности . Тогда далее рассматривается отрезок [a, c1]
и выбирается точка
Алгоритм
и
Условие завершения
Длина отрезка после n шагов
Количество итераций, требуемое для достижения заданной точности

Метод простых итераций для нелинейного уравнения
Исходное уравнение f (x) = 0 заменяется на x = ϕ(x)
Обычно это можно сделать просто выразив x из уравнения, например
Метод простых итераций (МПИ)
xn+1 = ϕ(xn)
Однако, не любая замена с последующей организацией итераций приводит к решению

Сходимость метода простых итераций
Теорема Лагранжа
f (x*) ≡ 0 x* = ϕ(x*)
x* = ϕ(x*)
xn+1 = ϕ(xn)
xn+1 – x*= ϕ(x*) – ϕ(xn) = ϕ’(ξ)(x* - xn)
Пусть x* - точное решение, тогда
xn+1 – x*=εn+1 – ошибка, получаемая на n + 1 –й итерации
Тогда эволюция ошибки:
εn+1 = ϕ’(ξ) · εn = (ϕ’(ξ))2 · εn-1 = … = (ϕ’(ξ))n+1 · ε0
Начальное приближение в любом случае выбирается с некоей ошибкой (сразу попасть в решение мы не можем).
Для того, чтобы эта ошибка убывала на итерациях необходимо, чтобы
q – скорость сходимости (максимальное по модулю значение производной)

Оценка числа итераций
Условие прекращения итераций:
Заданная точность
Невязка, при начальном приближении:
Необходимое число итераций для достижения заданной точности
Для прекращения итераций так же часто используют условие

Метод релаксации
Вид метода простой итерации при специальном выборе функции ϕ(x).
Численная производная по времени
В этом случае ϕ(x) = τ f (xn) + xn
МПИ сходится когда max|ϕ’(x)| < 1
Оптимальное значение итерационного параметра
Итерационный параметр
Пусть εn = xn – x* - погрешность на n-й итерации, тогда
Тогда уравнение для ошибки
= 0

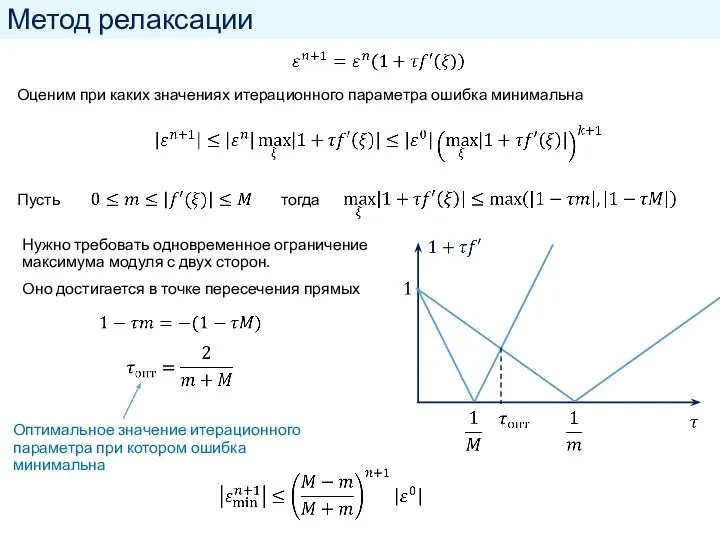
Метод релаксации
Оценим при каких значениях итерационного параметра ошибка минимальна
Пусть тогда
Нужно требовать одновременное ограничение максимума модуля с двух сторон.
Оно достигается в точке пересечения прямых
Оптимальное значение итерационного параметра при котором ошибка минимальна

Метод Ньютона для поиска решения
Ищем решение уравнения f (x) = 0, предполагаем, что на n + 1 - й итерации решение было найдено
Пренебрегаем слагаемыми второго порядка малости и получаем:
Метод Ньютона – частный случай МПИ. Условие сходимости с такой правой частью
Если вторая производная функции ограничена в некоторой окрестности решения f ’’< С2, а первая производная ограничена снизу f ’> С1 в этой же окрестности, то метод Ньютона сходится.
Метод Ньютона

Метод Ньютона
Теорема (о квадратичной сходимости метода Ньютона):
Пусть существуют две ограниченные производные функции f (x) и кроме того пусть существует
(f ’(x))-1, причем в некоторой окрестности корня U(x*) = {x: |x - x*| ≤ r} имеют место оценки
и кроме того, если
то метод Ньютона сходится квадратично, при этом
Доказательство:

Метод Ньютона
т.е.
Оценим убывание ошибки
Таким образом
Для сходимости метода Ньютона достаточно, чтобы были выполнены 2 условия:
Метод Ньютона сходится с квадратичной скоростью сходимости

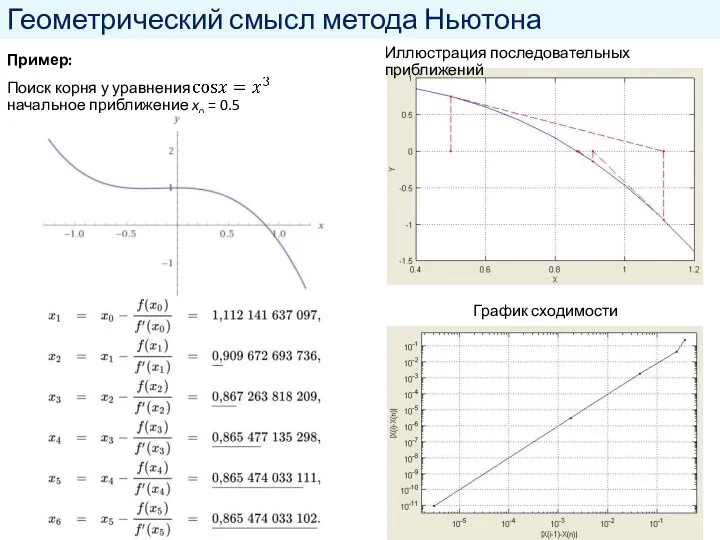
Геометрический смысл метода Ньютона
Пример:
Поиск корня у уравнения
начальное приближение x0 = 0.5
Иллюстрация последовательных приближений
График сходимости

Методы высших порядков
Итерационный процесс третьего порядка
Как и в методе Ньютона предполагаем, что после n + 1 шагов найдено решение
Разделим всё выражение на и для краткости обозначим
Получаем
Последний член является поправочным. Заменим в нем выражение xn+1 – xn на (-fn/f ’n)2 из метода Ньютона, получаем
Итерационный процесс четвертого порядка
Отметим, что итерационные методы высших порядок используются достаточно редко, вследствии повышенных требований к гладкости функций, необходимости вычисления производных высоких порядков и чувствительности к выбору начального приближения

Решение систем нелинейных уравнений: аксиомы нормы

Нормы векторов
В вычислительной математике широко распространены следующие нормы:
Максимальная или бесконечная норма (иногда используется название норма Чебышева)
l1 норма (или «Манхэттнновская норма» или «норма такси»)
Евклидова норма
Обозначения, принятые в МФТИ
Так же встречающиеся обозначения
Аксиомы нормы
Норма в векторном пространстве V над полем вещественных или комплексных чисел – это функционал ||.||: V → ꓣ, обладающий следующими свойствами.
1.
2.
3.

Нормы матриц
Опр.: Матричная норма ||A|| называется согласованной с векторной нормой ||x||, если выполняется неравенство
Норма матрицы должна удовлетворять следующим аксиомам
1.
2.
3.
Опр.: Матричная норма ||A|| называется подчиненной векторной норме ||x||, если выполняется

Свойства нормы
Опр.: Матричная норма ||A|| называется субмультипликативной, если
Замечание: если норма ||A|| подчинена какой-либо векторной норме ||x||, то она субмультипликативна
Свойства нормы
Если норма ||A|| подчинена кокой-либо норме ||x||, то она с ней согласована:

Используемые нормы матриц
Определим выражения для норм матриц

Евклидова норма
Воспользуемся связью между евклидовой нормой вектора и скалярным произведением
А так же свойством, что ортогональные матрицы U-1 = UT сохраняют скалярное произведение
Осуществим сингулярное разложение матрицы A
где
Тогда
Если A = AT, то

Решение систем нелинейных уравнений: аксиомы нормы

Метод простых итераций для систем
Для численного решения многомерных систем нелинейных уравнений могут быть использованы только обобщения одномерных методов.
Задача состоит в поиске решения системы нелинейных уравнений
Аналогично МПИ для одномерного случая представляем систему в виде:

Метод простых итераций
Доказательство:
Поэтому
При p > n имеем цепочку неравенств

Метод простых итераций
Поскольку n произвольно, то
Замечание: При n = 0
Таким образом все приближения принадлежат области

Метод простых итераций
Доказательство: Пусть выбрано нулевое приближение, а далее
Погрешность в k-ой компоненте
l – направление соединения точек us и u* ξk некоторая точка на этом отрезке многомерного пространства

Метод Ньютона для систем
В этом случае матрица Якоби отличается от матрицы метода простых итераций
Для ε ~ 10-5 - 10-6 это означает 10 верных знаков для u.
Самая трудоемкая операция в методе Ньютона – вычисление обратной матрицы. Поэтому иногда используют упрощенный метод Ньютона:
Матрица Якоби обращается один раз. Метод приемлем, т.к. начальное приближение выбирается достаточно близко к корню.