Содержание
- 2. ЧТО ТАКОЕ ПРОГРЕССИЯ? Термин «прогрессия» имеет латинское происхождение (progression), что означает «движение вперед» и был введен
- 3. ЧТО ОБЩЕГО В ПОСЛЕДОВАТЕЛЬНОСТЯХ? 2, 6, 10, 14, 18, …. 11, 8, 5, 2, -1, ….
- 4. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с
- 5. РАЗНОСТЬ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ Число d, показывающее, на сколько следующий член последовательности отличается от предыдущего, называется разностью
- 6. СВОЙСТВА ПРОГРЕССИИ 2, 6, 10, 14, 18, …. 11, 8, 5, 2, -1, …. 5, 5,
- 7. ЗАДАЧА На складе 1 числа было 50 тонн угля. Каждый день в течение месяца на склад
- 8. ФОРМУЛА N-ОГО ЧЛЕНА a1 a2=a1+d a3=a2+d=a1+2d a4=a3+d=a1+3d …………………….. an=an-1+d=a1+(n-1)d an=a1+d (n-1)
- 9. ПРИМЕР 1. Последовательность (аn)-арифметическая прогрессия. Найдите а81, если а1=20 и d=3. Решение: Воспользуемся формулой n-ого члена
- 10. ХАРАКТЕРИСТИЧЕСКОЕ СВОЙСТВО АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ Пусть an – искомый член последовательности. Воспользуемся тем, что разность между соседними
- 11. ЗАДАЧА Последовательность (аn)- арифметическая прогрессия. Найдите а21, если а1=5,8 и d=-1,5. Решение: Воспользуемся формулой n-ого члена
- 12. ИНТЕРЕСНЫЙ ФАКТ Любая арифметическая прогрессия может быть задана формулой an=kn+b, где k и b – некоторые
- 14. Скачать презентацию











 Презентация на тему Объем пирамиды
Презентация на тему Объем пирамиды  От перестановки множителей произведение не изменяется
От перестановки множителей произведение не изменяется Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс
Презентация на тему Платоновы тела Правильные выпуклые многогранники 10 класс  preobrazovanie
preobrazovanie Третий признак равенства треугольников
Третий признак равенства треугольников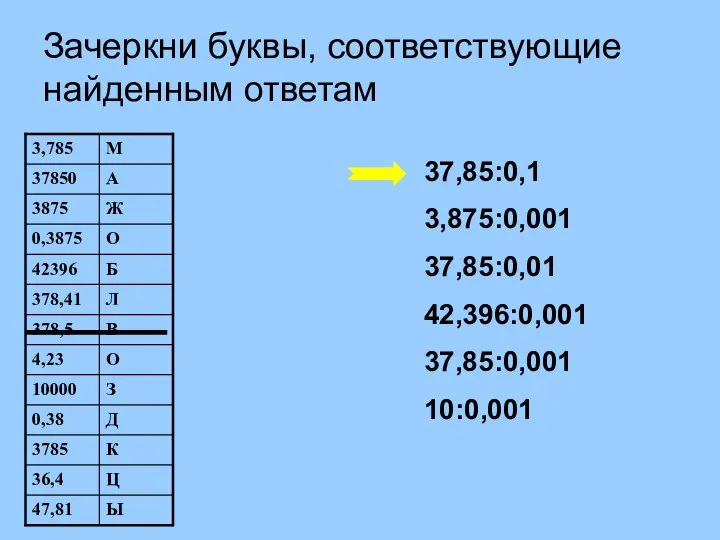 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Уравнение касательной
Уравнение касательной Теорема Пифагора
Теорема Пифагора Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Презентация на тему Округление натуральных чисел (5 класс)
Презентация на тему Округление натуральных чисел (5 класс)  Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности
Неисключенные остатки систематической погрешности. Статистическая обработка однократных наблюдений. Случайные погрешности Геометрическое место точек. 7 класс
Геометрическое место точек. 7 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов История математики в лицах великих учёных
История математики в лицах великих учёных Страничка для любознательных - задания творческого и поискового характера
Страничка для любознательных - задания творческого и поискового характера Эвристические приемы. Алгебра 8 класс
Эвристические приемы. Алгебра 8 класс Число 10
Число 10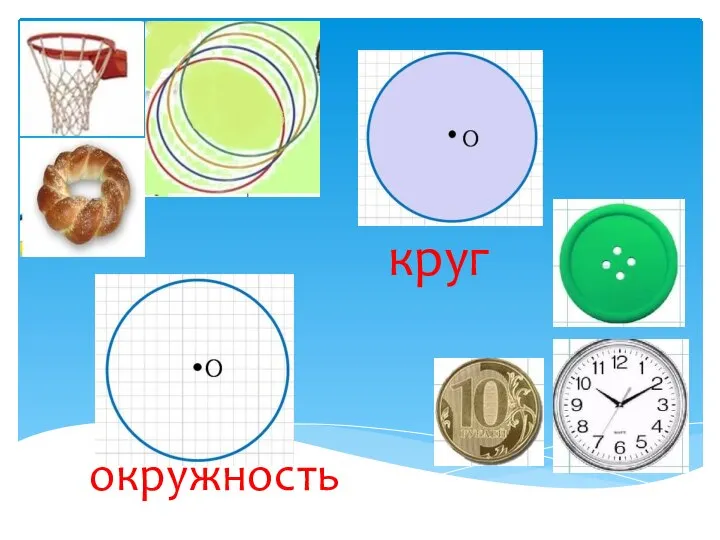 Круг, окружность
Круг, окружность Уравнение с параметром
Уравнение с параметром Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Презентация на тему Решение комбинаторных задач и задач по теории вероятности
Презентация на тему Решение комбинаторных задач и задач по теории вероятности  Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Задачи на кратное сравнение (закрепление)
Задачи на кратное сравнение (закрепление) Признаки параллельности прямых
Признаки параллельности прямых Тренировочные задания (графическое представление данных)
Тренировочные задания (графическое представление данных) Теория Пределов
Теория Пределов Стереометрия. Школьный курс
Стереометрия. Школьный курс