Поразрядная конъюнкция. Способы решения задания ЕГЭ №15 (№18)

Выдержка из кодификатора элементов содержания
Знания о:
формах мышления (понятии, суждении, умозаключении);
основных логических функциях;
законах логики;
методах решения логических уравнений и систем логических уравнений;
базовых логических элементов компьютера (Сумматоре, триггере).
Умения
построить диаграммы Эйлера-Венна.
построить таблицы истинности для сложных высказываний.
строить и преобразовывать логические выражения.
анализировать схемы, построенные с использованием базовых логических элементов компьютера и строить для них таблицы истинности.

Основные типы заданий №18

Формулы логики
A. Свойства 0, 1 и отрицания
Свойства 0 и 1
Свойства отрицания

Формулы логики
Б. Дизъюнкция и конъюнкция
Сочетательный закон
Переместительный закон
Закон повторения
Распределительный закон
Правила де Моргана

Формулы логики
В. Импликация и эквивалентность
Определение импликации
Свойства импликации
Эквивалентность

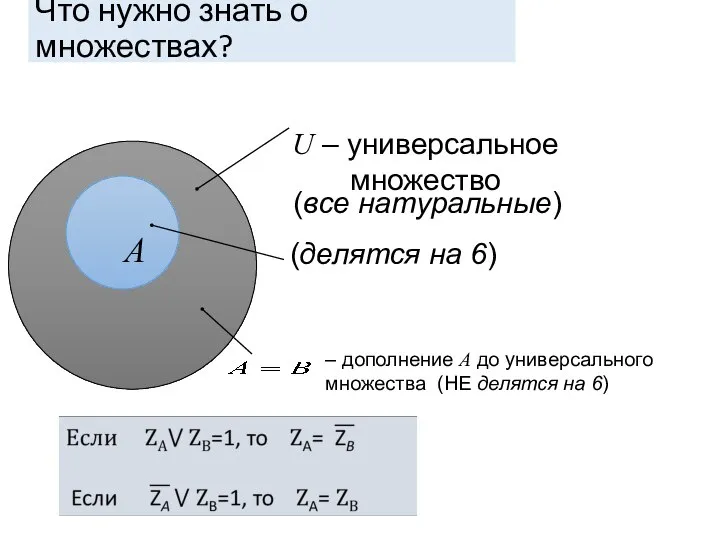
Что нужно знать о множествах?
A
(все натуральные)
U – универсальное
множество
– дополнение A до универсального множества (НЕ делятся на 6)

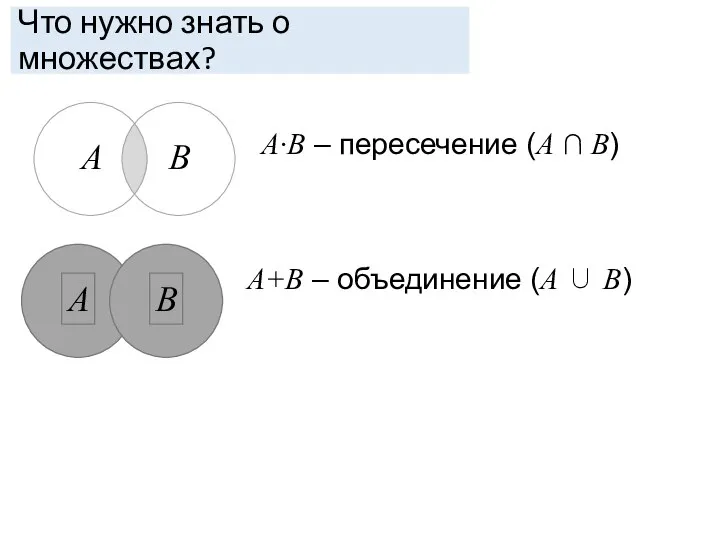
Что нужно знать о множествах?
A·B – пересечение (A ∩ B)
A+B – объединение (A ∪ B)

Множества и логические функции
Множество задаётся логической функцией
x ∈ A
⇔ x ∈ A·B
⇔ x ∈ A+B
⇔ A(x) = 1

Свойства:
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
Пример: Определить значение логического выражения
X & 29 = 0 → X & 5 = 0
(Истинно или Ложно? )
Сделаем замену: Z29 → Z5
Z29 → Z5 = 1 (истине), тогда, когда:
29 = 111012
5 = 1012
единичные биты двоичного числа 5 входят в единичные биты двоичного числа 29 (совпадают с ними)
таким образом, получили:
Z29 → Z5 = 1 (истинно)

1 способ решения:

В
А

2 способ решения:
Ответ:38

3 способ решения:
1
1
1
В x хоть в одной желтой ячейки есть 1
В x хоть в одной желтой ячейки есть 1
Ответ:38

Самостоятельная работа
15 мин

Самостоятельная работа
Для какого наименьшего неотрицательного целого числа формула тождественно истинна (т. е. принимает значение при любом неотрицательном целом значении переменной ?
Задание №1
Задание №2
x&49 ≠ 0 → (x&41 = 0 → x&А ≠ 0) =1
Задание №3
x&9 = 0 → (x&19 ≠ 0 → x&А ≠ 0)=1

Домашняя работа