Содержание
- 2. Вопросы Функциональное и оптимальное проектирование Задачи оптимального проектирования Методы принятия решений в задачах параметрической оптимизации Принятие
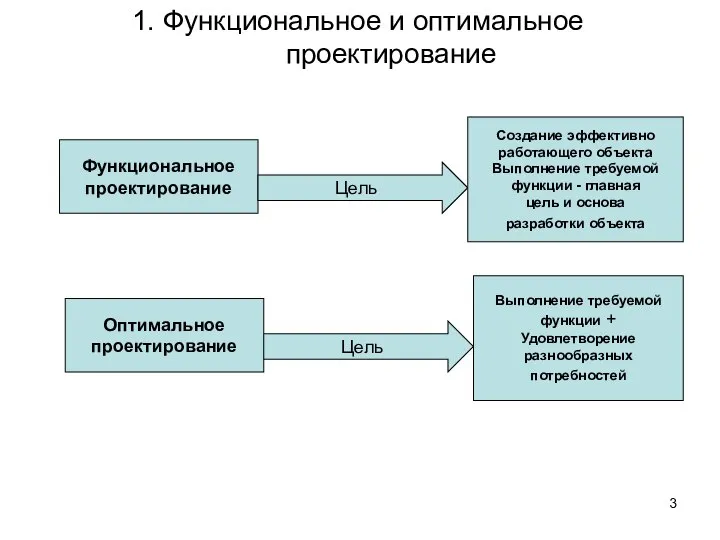
- 3. 1. Функциональное и оптимальное проектирование Функциональное проектирование Цель Создание эффективно работающего объекта Выполнение требуемой функции -
- 4. Оптимальное проектирование (критериальное, вариантное проектирование) - проектирование, целью которого является не только поиск функционально эффективных решений,
- 5. 2. Задачи оптимального проектирования Рекомендуемые к исполнению решения должны быть: обоснованными, своевременными, директивными (обязательными к исполнению),
- 6. Человек, который имеет право выбирать окончательное решение, несет за него ответственность, заинтересован в решении проблемы, называется
- 7. Выбор возможен одним из следующих способов: случайным образом (способом необъяснимым и независящим от условий задачи), волевым
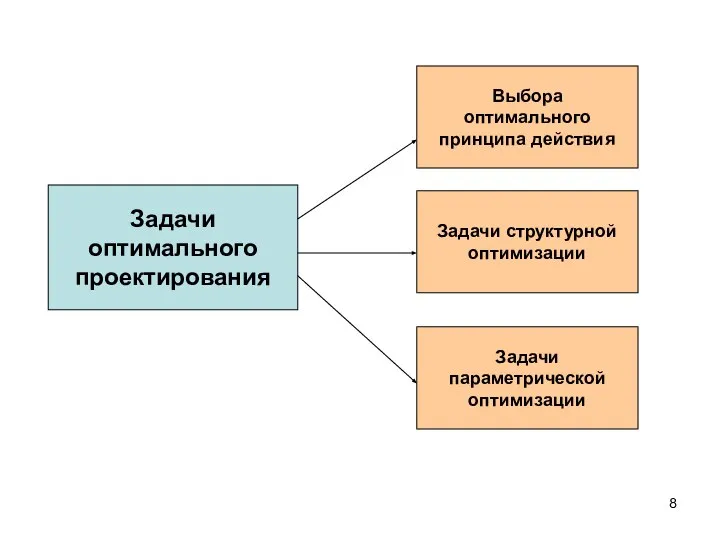
- 8. Задачи оптимального проектирования Выбора оптимального принципа действия Задачи структурной оптимизации Задачи параметрической оптимизации
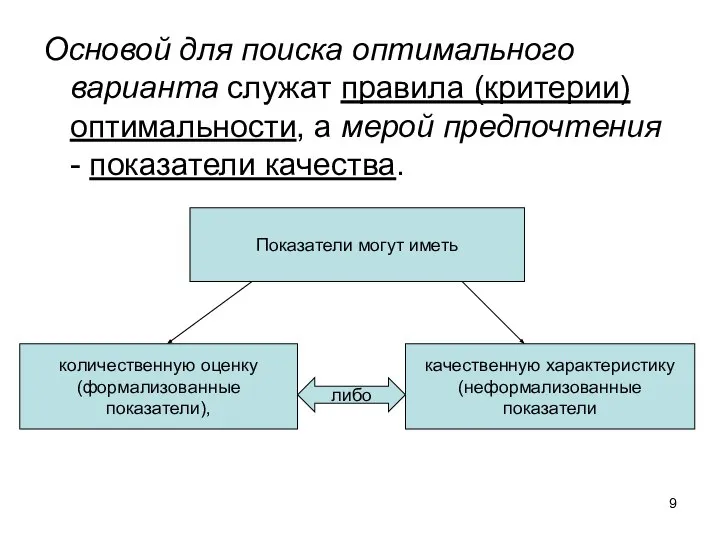
- 9. Основой для поиска оптимального варианта служат правила (критерии) оптимальности, а мерой предпочтения - показатели качества. Показатели
- 10. Для удобства и однозначности восприятия критерии Кi (где i=1,..., m и m - число критериев) нормируют,
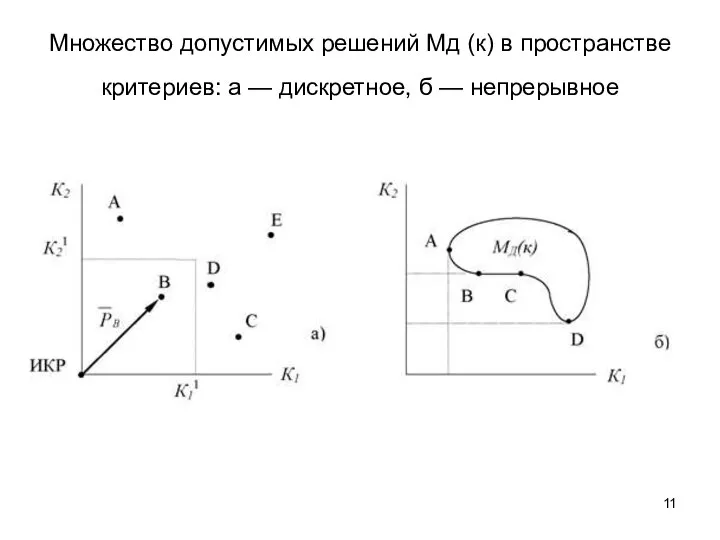
- 11. Множество допустимых решений Мд (к) в пространстве критериев: а — дискретное, б — непрерывное
- 12. 3. Методы принятия решений в задачах параметрической оптимизации Однокритериальные задачи: поиска экстремума алгебраической функции зависимости критерия
- 13. Задачи многокритериальной оптимизации Способы поиска решений выделение области компромиссов и отбрасывание заведомо неудовлетворительных решений; Замена критериев
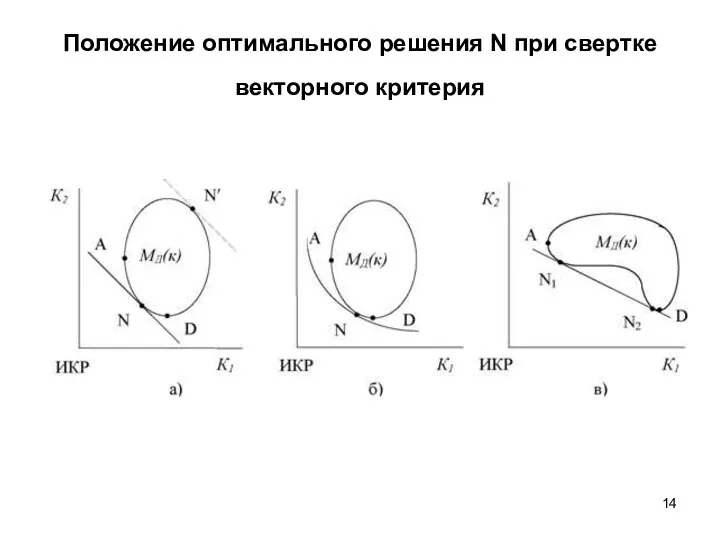
- 14. Положение оптимального решения N при свертке векторного критерия
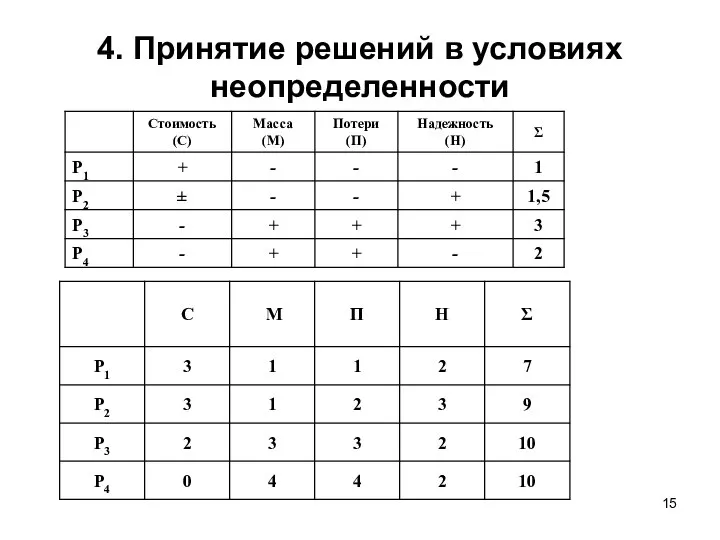
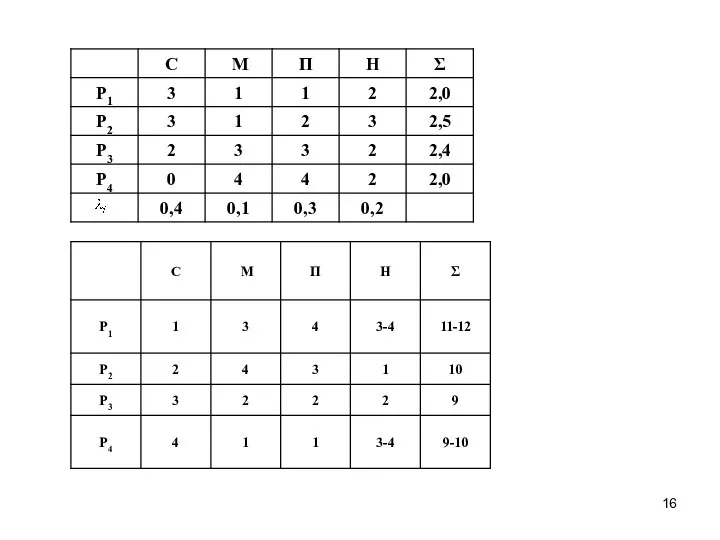
- 15. 4. Принятие решений в условиях неопределенности
- 18. Скачать презентацию








 Морской бой
Морской бой Преобразование целого выражения в многочлен
Преобразование целого выражения в многочлен Таблица умножения
Таблица умножения Pervoobraznaya
Pervoobraznaya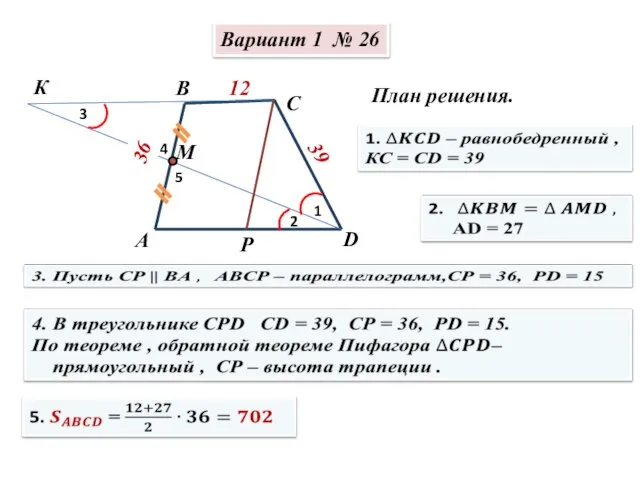 Сборник И.В. Ященко. Решение заданий №26
Сборник И.В. Ященко. Решение заданий №26 Решение задач на применение признаков подобия треугольников
Решение задач на применение признаков подобия треугольников 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Парадокс раздела ставки
Парадокс раздела ставки Теорема Пифагора
Теорема Пифагора Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями
Сложнние и вычитание алгебраических дробей с одинаковыми знаменателями Иррациональные неравенства и способы их решения
Иррациональные неравенства и способы их решения Компетентность
Компетентность Логические задачи. 1 класс
Логические задачи. 1 класс Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Теорема Фалеса
Теорема Фалеса Умники и умницы. Викторина по математике
Умники и умницы. Викторина по математике Занимательные задачи
Занимательные задачи Лингвистика в математике
Лингвистика в математике Нахождение площади фигур и объемов тел
Нахождение площади фигур и объемов тел Второй признак подобия треугольников
Второй признак подобия треугольников Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8
Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8 L_3_U
L_3_U Повторение курса 5 класса
Повторение курса 5 класса Задачи с дробями
Задачи с дробями Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта
Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта Решение задач с помощью геометрии
Решение задач с помощью геометрии