что областью определения показательной функции является R?
3. Является ли убывающей функция y = 2х ?
4. Верно ли, что показательная функция y = ?х принимается наибольшее значение в некоторой точке x0?
5. Представить в виде степени:
3-2 · 81
1. Является ли показательной функция:
y = x5 + 2?
2. Верно ли, что график показательной функции проходит через точку с координатами (0;1)?
3. Является ли возрастающей функция y = (0,3)х ?
4. Верно ли, что показательная функция y = ?х принимается в некоторой точке значение равное нулю?
5. Представить в виде степени:
2-2 · 32
Математический диктант
Вариант 1
Вариант 2




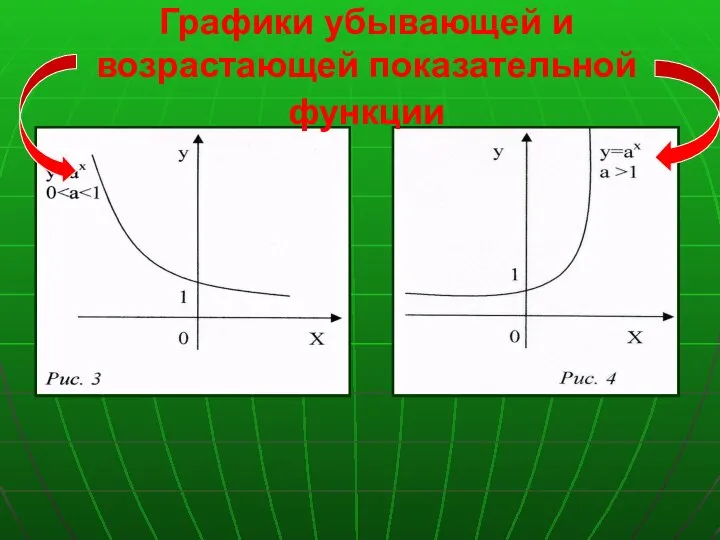










 Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Предпосылки МНК для парной линейной регрессии. Тема 4
Предпосылки МНК для парной линейной регрессии. Тема 4 Задачи. Урок 20
Задачи. Урок 20 Понятие неравенство
Понятие неравенство Площадь полной поверхности пирамиды
Площадь полной поверхности пирамиды Преобразование простейших тригонометрических выражений
Преобразование простейших тригонометрических выражений Информационные технологии образовании
Информационные технологии образовании Множество
Множество Час занимательной математики
Час занимательной математики Занимательные задачи (4 класс)
Занимательные задачи (4 класс) Задача по математике (1 класс)
Задача по математике (1 класс) Приемы вычитания с переходом через разряд вида 35 - 7
Приемы вычитания с переходом через разряд вида 35 - 7 Площадь фигур
Площадь фигур Вычитание дроби из целого числа (урок 116)
Вычитание дроби из целого числа (урок 116) Построение сечения
Построение сечения Векторный анализ -теория поля. Типы векторных полей. Лекция 18
Векторный анализ -теория поля. Типы векторных полей. Лекция 18 ДПА 11 класс Первообразная и интеграл
ДПА 11 класс Первообразная и интеграл Треугольники и их виды
Треугольники и их виды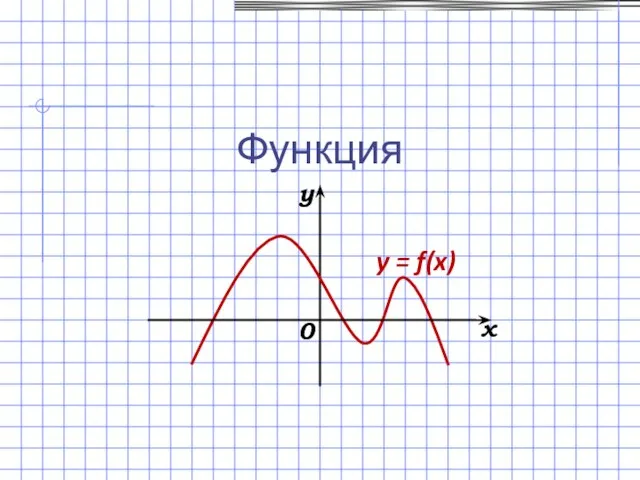 Функция y = f(x)
Функция y = f(x) Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5? Понятие производной
Понятие производной Позиционные задачи
Позиционные задачи Байесовский анализ и сети Байеса
Байесовский анализ и сети Байеса Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Логарифмические неравенства. Решение заданий
Логарифмические неравенства. Решение заданий Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Comparative of superlative
Comparative of superlative Натуральый степень, свойства, показатель
Натуральый степень, свойства, показатель