Объемы прямой призмы и цилиндра (11 класс)

ЭПИГРАФ:
Первое условие, которое надлежит
выполнять в математике, –
это быть точным, второе – быть
ясным и, насколько можно,
простым.
Лазар Карно
(французский государственный и военный
деятель, инженер и ученый)

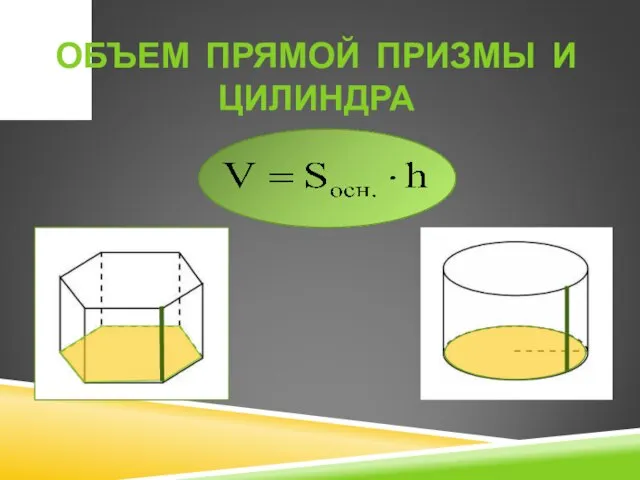
повторить формулы для вычисления объема прямой призмы и цилиндра;
учиться применять формулы для вычисления объема прямой призмы и цилиндра при решении задач;
рассмотреть задачи на вычисление объема призмы и цилиндра.

ОБЪЕМ ПРЯМОЙ ПРИЗМЫ И ЦИЛИНДРА

СВЕДЕНИЯ ИЗ ПЛАНИМЕТРИИ

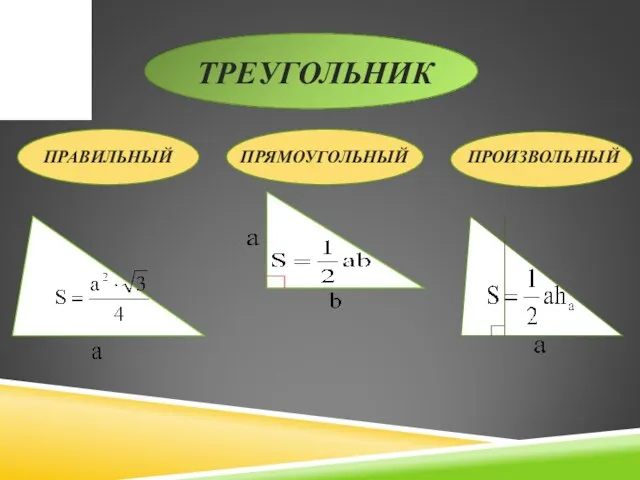
ТРЕУГОЛЬНИК
ПРАВИЛЬНЫЙ
ПРЯМОУГОЛЬНЫЙ
ПРОИЗВОЛЬНЫЙ

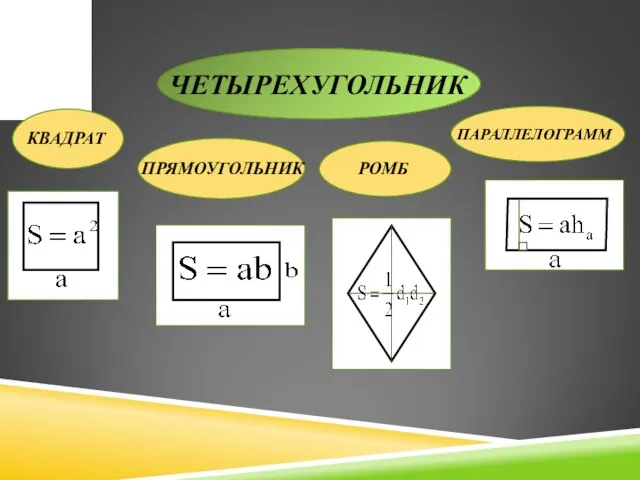
ЧЕТЫРЕХУГОЛЬНИК
КВАДРАТ
ПРЯМОУГОЛЬНИК
РОМБ
ПАРАЛЛЕЛОГРАММ

ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК

НЕКОТОРЫЕ ОТНОШЕНИЯ ПОДОБИЯ
Отношение периметров подобных многоугольников равно коэффициенту подобия.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Отношение объемов подобных тел равно кубу коэффициента подобия.

ОБЪЕМ ПРИЗМЫ

Основанием прямой треугольной призмы служит прямоугольный тре­угольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем приз­мы.
ЗАДАЧА 1

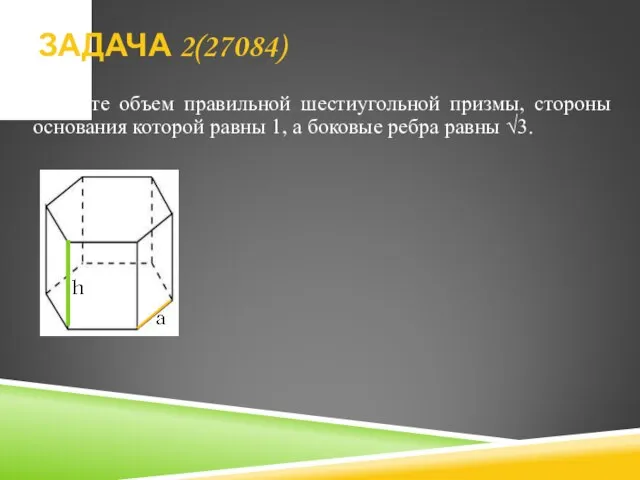
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны √3.
ЗАДАЧА 2(27084)

ЗАДАЧА 3 (27048)
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

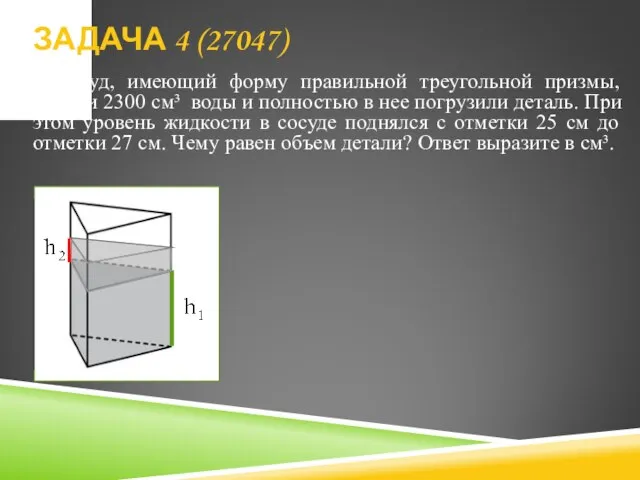
В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см³.
ЗАДАЧА 4 (27047)

ОБЪЕМ ЦИЛИНДРА

В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
ЗАДАЧА 5(27091)

Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
ЗАДАЧА 6(27053)

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/π.
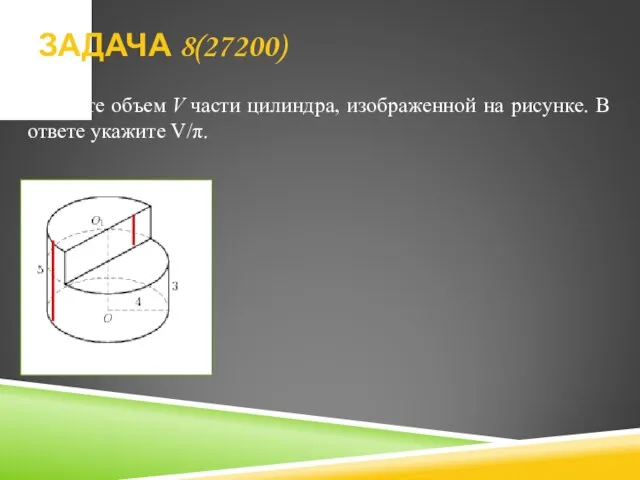
ЗАДАЧА 7(27199)

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/π.
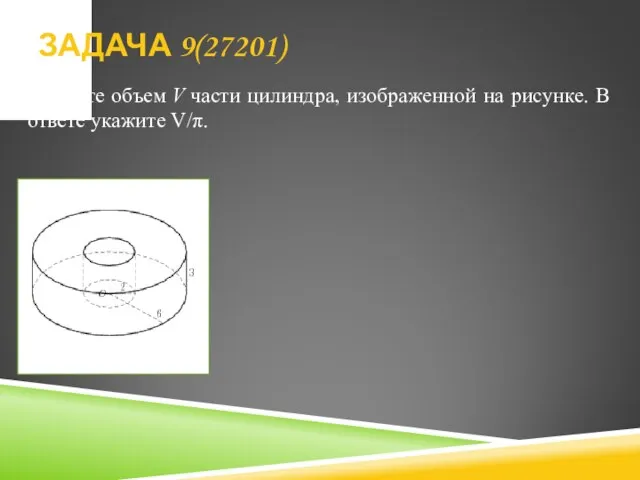
ЗАДАЧА 8(27200)

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/π.
ЗАДАЧА 9(27201)