Содержание
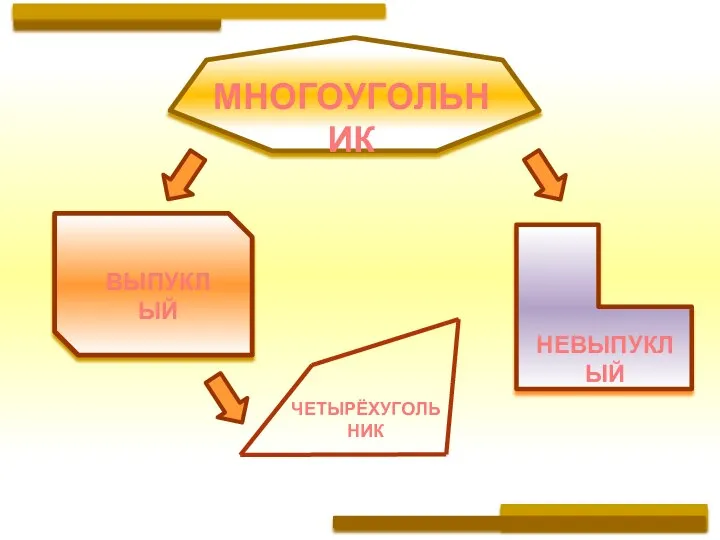
- 2. МНОГОУГОЛЬНИК ВЫПУКЛЫЙ НЕВЫПУКЛЫЙ
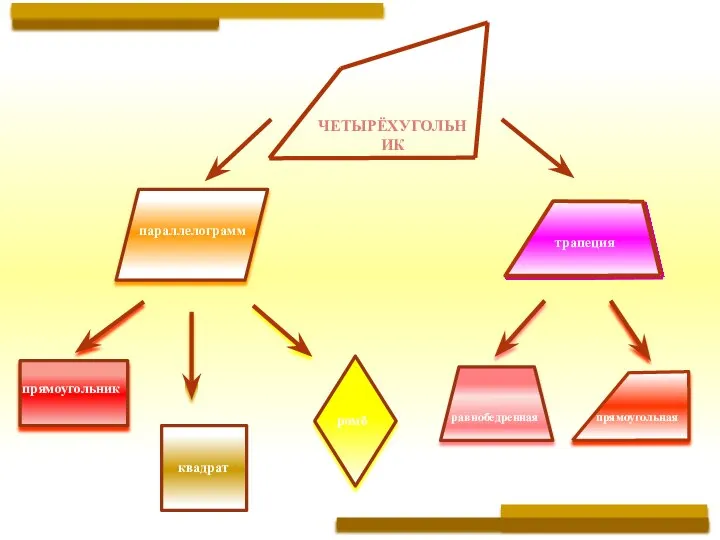
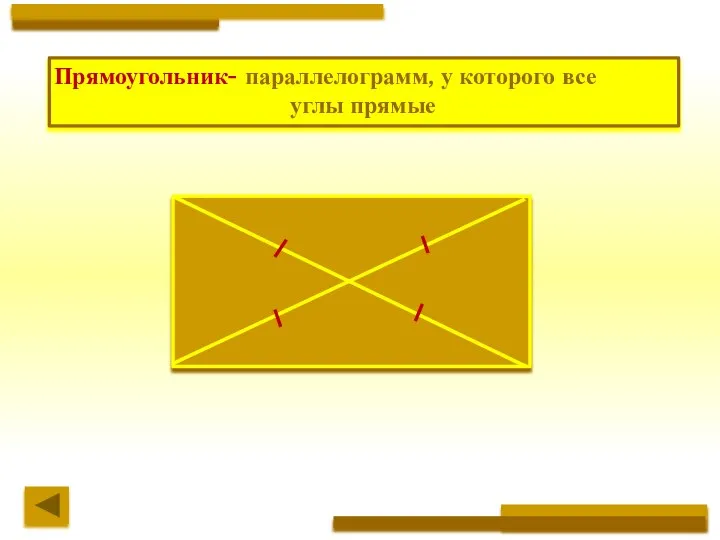
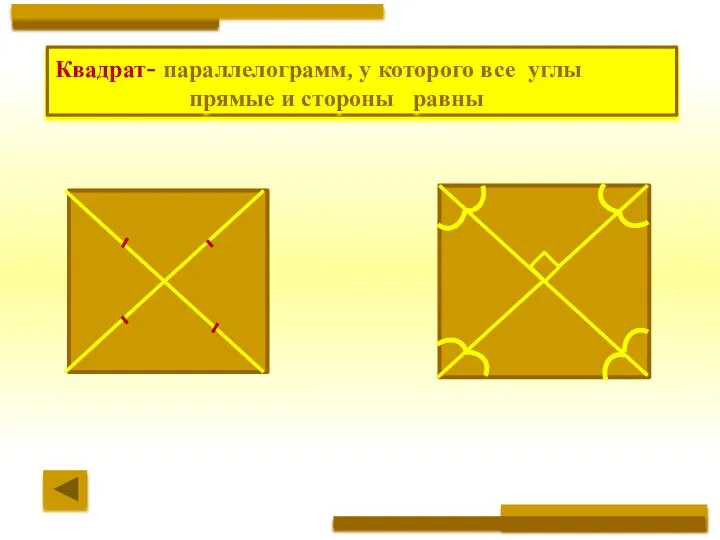
- 3. ЧЕТЫРЁХУГОЛЬНИК параллелограмм прямоугольник трапеция квадрат ромб прямоугольная равнобедренная
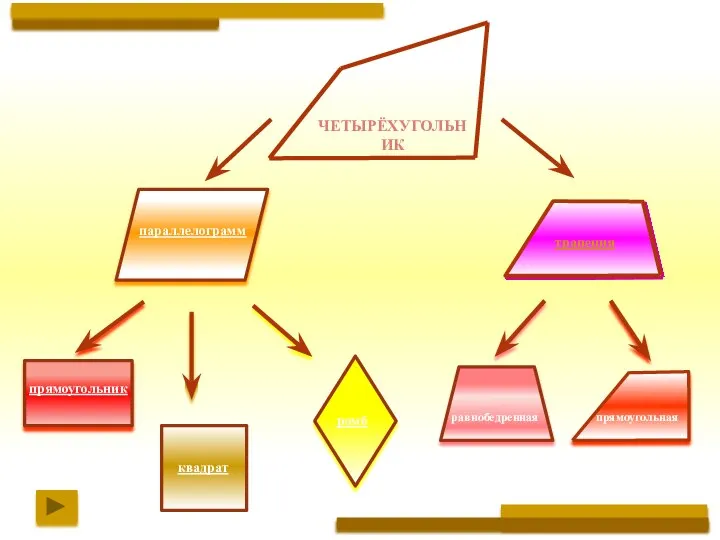
- 4. параллелограмм прямоугольник трапеция квадрат ромб прямоугольная равнобедренная
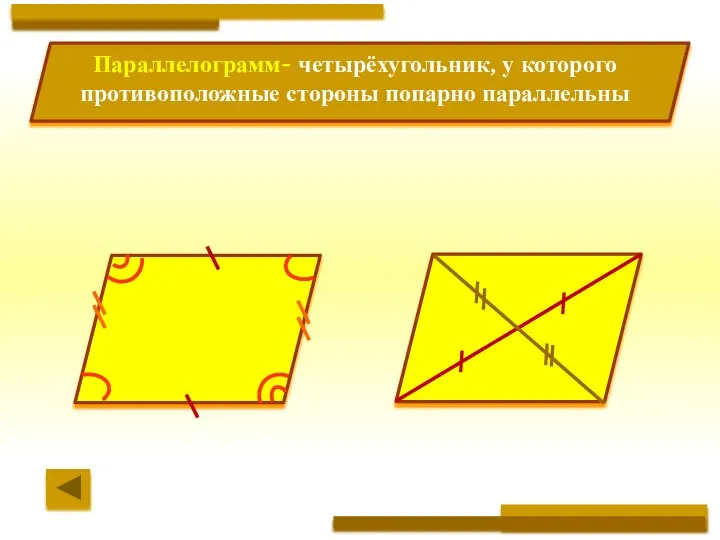
- 5. Параллелограмм- четырёхугольник, у которого противоположные стороны попарно параллельны
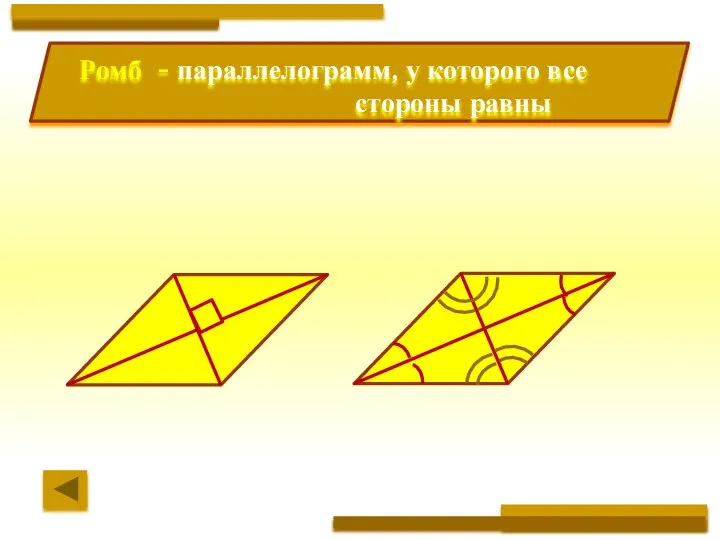
- 7. Ромб - параллелограмм, у которого все стороны равны
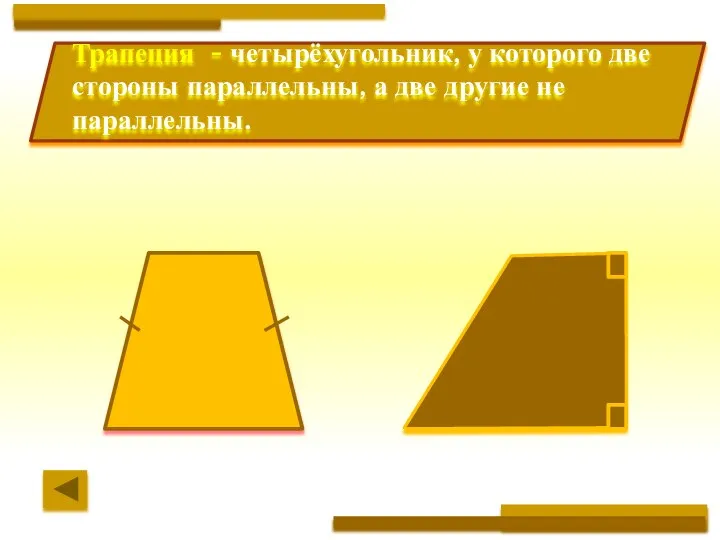
- 9. Трапеция - четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
- 10. Графический диктант Если диагонали параллелограмма равны, то он может быть только прямоугольником. Если диагонали параллелограмма равны
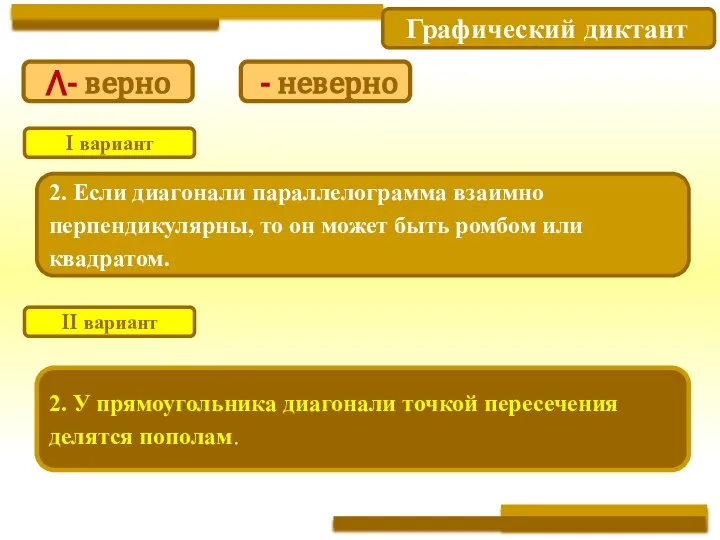
- 11. Графический диктант 2. Если диагонали параллелограмма взаимно перпендикулярны, то он может быть ромбом или квадратом. 2.
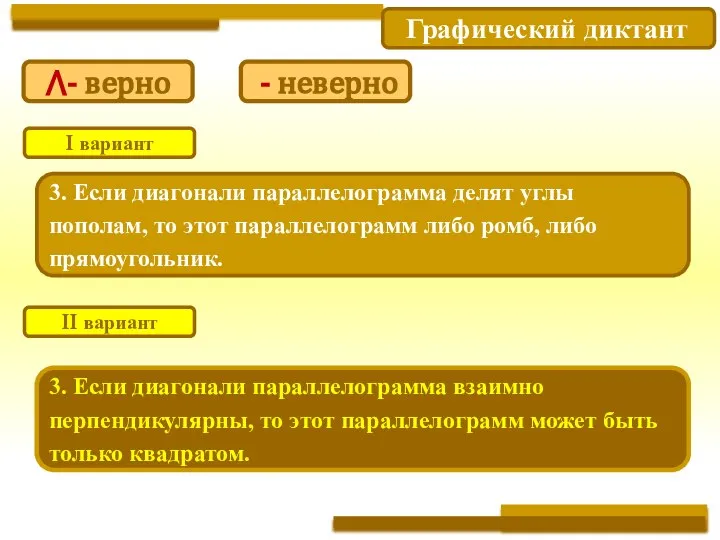
- 12. Графический диктант 3. Если диагонали параллелограмма делят углы пополам, то этот параллелограмм либо ромб, либо прямоугольник.
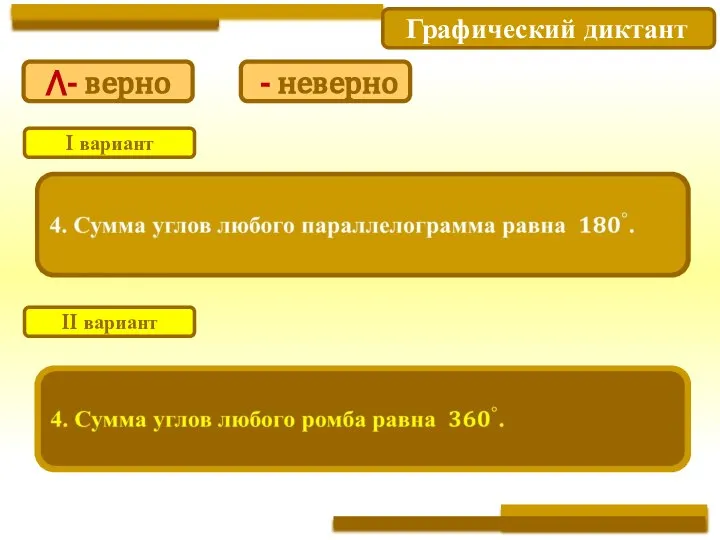
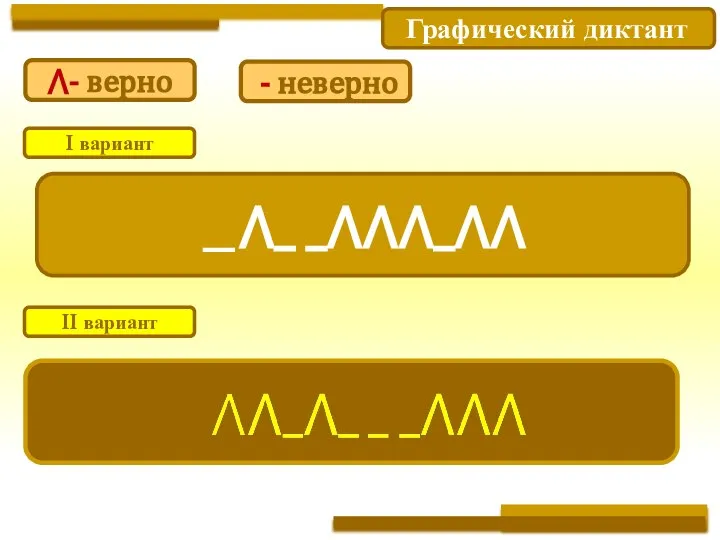
- 13. Графический диктант I вариант II вариант ⋀- верно - неверно
- 14. Графический диктант 5. Если стороны параллелограмма 12 см и 14 см, то это соседние стороны. 5.
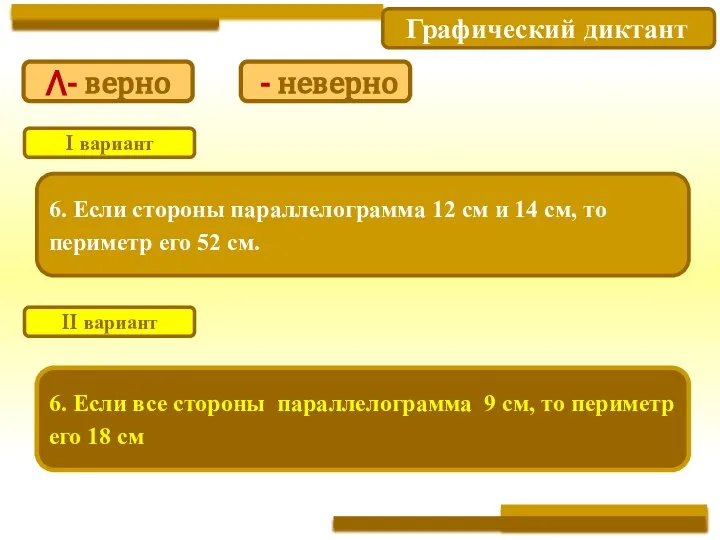
- 15. Графический диктант 6. Если стороны параллелограмма 12 см и 14 см, то периметр его 52 см.
- 16. Графический диктант I вариант II вариант ⋀- верно - неверно
- 17. Графический диктант 8. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник параллелограмм. I
- 18. Графический диктант 9. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник параллелограмм. 9. У
- 19. Графический диктант 10. У ромба диагонали делят углы пополам. I вариант II вариант ⋀- верно -
- 20. Графический диктант _⋀_ _⋀⋀⋀_⋀⋀ I вариант II вариант ⋀- верно - неверно
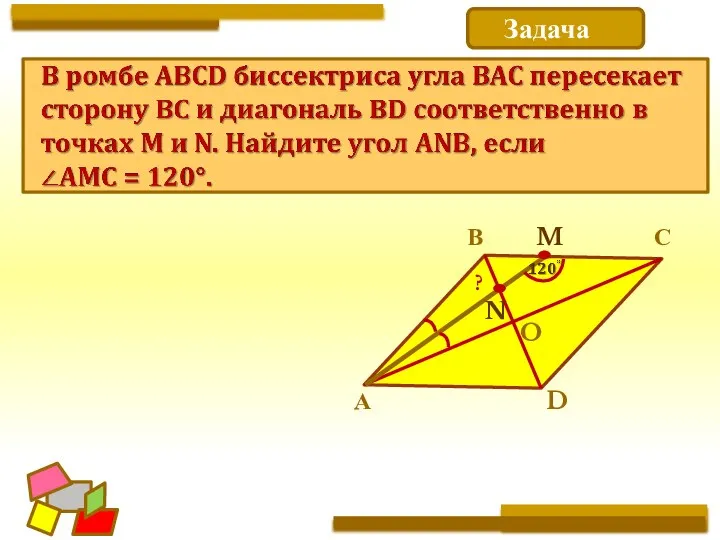
- 21. Задача А В С O D N M ?
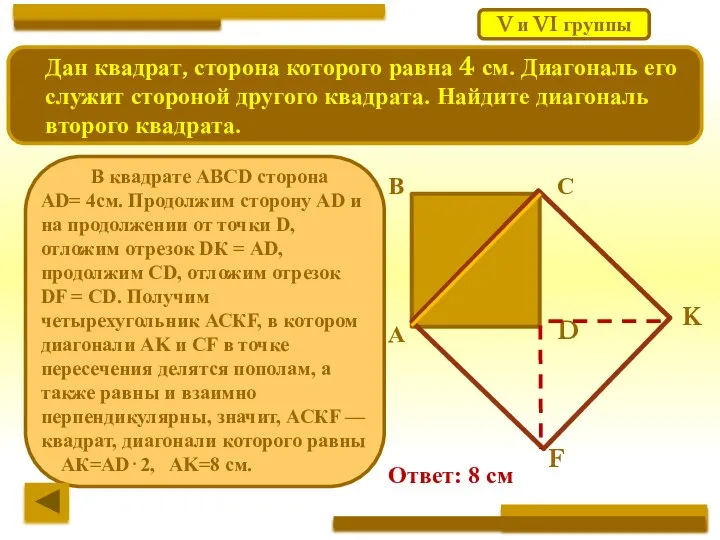
- 22. Работа в группах Дан квадрат, сторона которого равна 4 см. Диагональ его служит стороной другого квадрата.
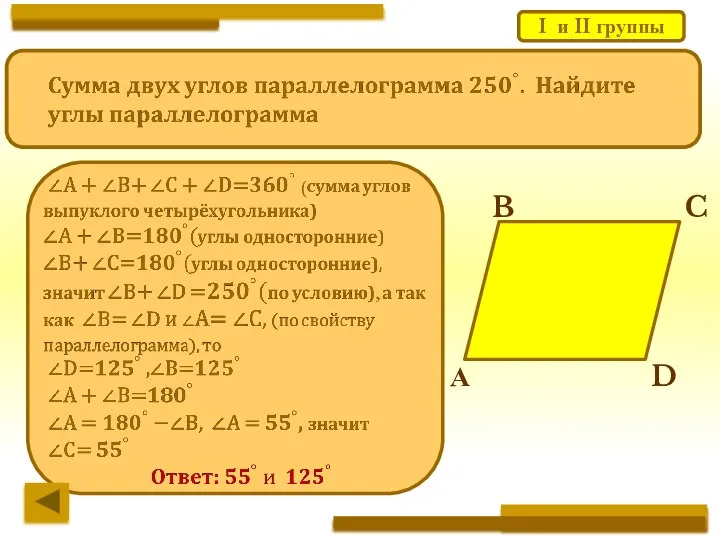
- 23. I и II группы
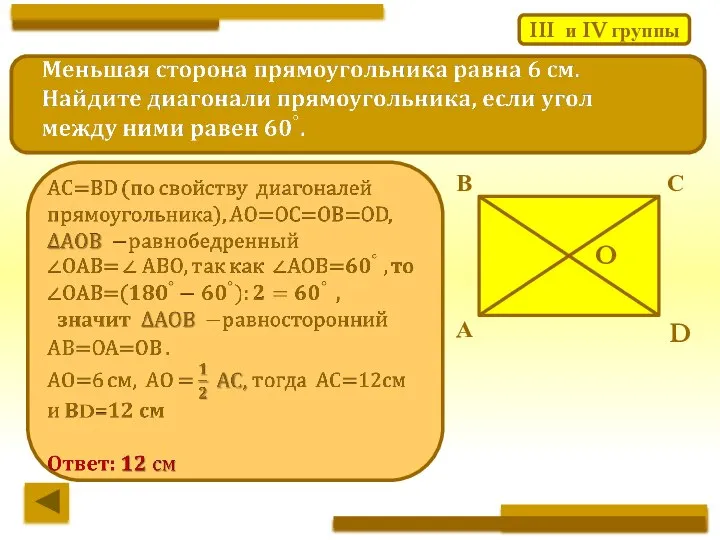
- 24. III и IV группы А В С O D
- 25. Дан квадрат, сторона которого равна 4 см. Диагональ его служит стороной другого квадрата. Найдите диагональ второго
- 26. Домашнее задание 1. В параллелограмме MNPQ через точку О пересечения диагоналей проходит прямая , пересекающая NP
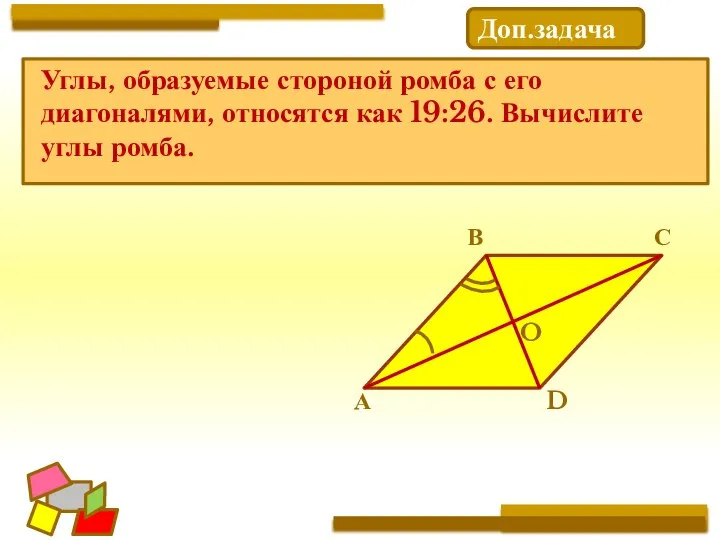
- 27. Углы, образуемые стороной ромба с его диагоналями, относятся как 19:26. Вычислите углы ромба. Доп.задача А В
- 29. Скачать презентацию




 Умножение и деление степеней
Умножение и деление степеней Средняя квадратическая величина
Средняя квадратическая величина Год, месяц, сутки
Год, месяц, сутки Угол между векторами
Угол между векторами Понятие треугольника
Понятие треугольника Музыкалық аспаптарға
Музыкалық аспаптарға Задачи на нахождение двух чисел по их сумме и разности
Задачи на нахождение двух чисел по их сумме и разности Создание и применение мультимедийных презентаций на уроках математики
Создание и применение мультимедийных презентаций на уроках математики Игра в стручки
Игра в стручки Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Презентация на тему Упрощение выражений
Презентация на тему Упрощение выражений  Простые задачи на умножение и деление
Простые задачи на умножение и деление Теорема Безу (теорема об остатке и разложение на множители)
Теорема Безу (теорема об остатке и разложение на множители) Карты Карно. Решение заданий
Карты Карно. Решение заданий Письменное умножение двузначных и трехзначных чисел на однозначное число
Письменное умножение двузначных и трехзначных чисел на однозначное число Число и цифра 2
Число и цифра 2 Решение систем линейных неравенств
Решение систем линейных неравенств Степень с отрицательным показателем
Степень с отрицательным показателем Урок в лесной школе
Урок в лесной школе Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра - тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Вписанная окружность
Вписанная окружность Задачи с параметром на ЕГЭ (задача 18). Линейные уравнения
Задачи с параметром на ЕГЭ (задача 18). Линейные уравнения Математическое моделирование в среде электронных таблиц MS Excel
Математическое моделирование в среде электронных таблиц MS Excel Построение сечений
Построение сечений Все действия с десятичными дробями
Все действия с десятичными дробями Алгебра. Урок-тренинг
Алгебра. Урок-тренинг Презентация на тему Начальные геометрические сведения
Презентация на тему Начальные геометрические сведения  Окружность в аксонометрии. 8 класс
Окружность в аксонометрии. 8 класс