Содержание
- 2. План занятия: Численное решение задачи Коши, -Пример №1. -Пример №2. -Пример №3
- 3. Что такое задача Коши и зачем она нужна?
- 5. ПРИМЕР №1: Феофан бросил утюг вертикально вверх. Используя MatLab, определите каких максимальных высот достигнет утюг, если
- 6. Решение: V=V0-gt. Обозначим: высоту грузика= y(1) Скорость грузика (производная от высоты грузика)= y(2) Тогда исходное уравнение
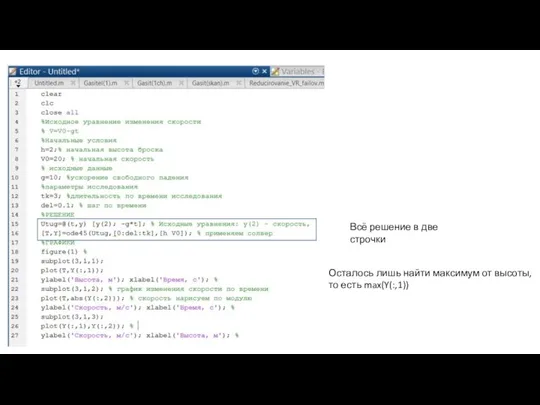
- 7. Всё решение в две строчки Осталось лишь найти максимум от высоты, то есть max(Y(:,1))
- 8. В последний момент Феофан ловко увернулся от падающего утюга, порвав подштанники. Данный прецедент не расстроил Феофана
- 9. Решение: В общем виде уравнение выглядит следующим образом: mx’’+Cx’+Kx = F (Даже Феофан может расшифровать что
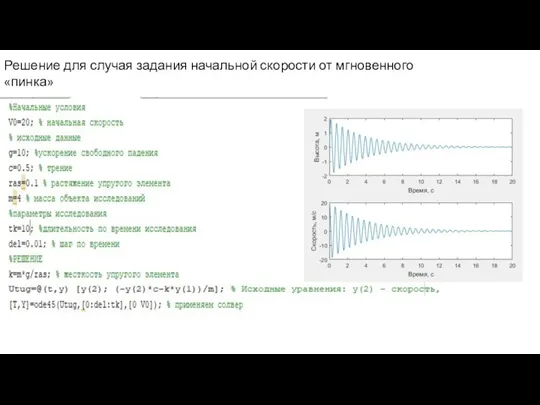
- 10. Решение для случая задания начальной скорости от мгновенного «пинка»
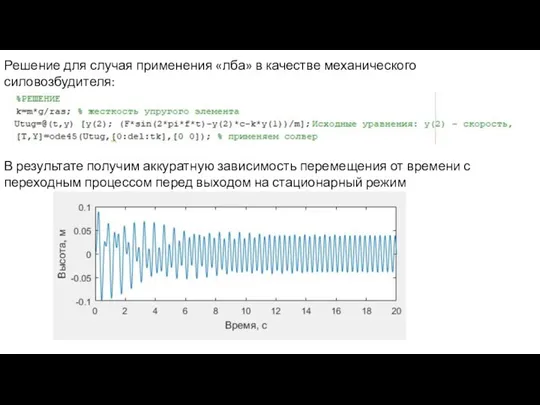
- 11. Решение для случая применения «лба» в качестве механического силовозбудителя: В результате получим аккуратную зависимость перемещения от
- 12. Накопленный Феофаном научный опыт дал свои плоды, и вскоре юный естествоиспытатель добрался до старших курсов МГТУ.
- 13. Алгоритм решения: Решим задачу без учета пружины «2». С момента когда сжатие пружины «1» стало больше
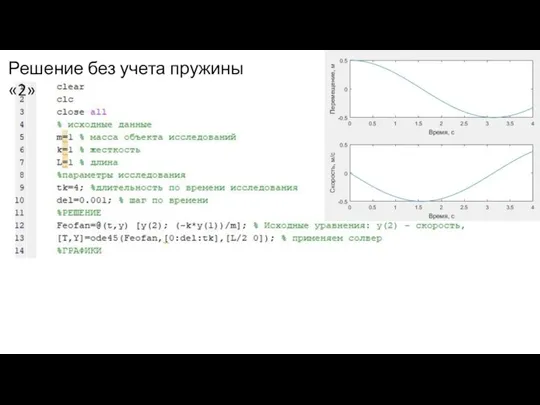
- 14. Решение без учета пружины «2»
- 15. Определим момент, с которого жесткость должна увеличиться: Из массива перемещений вычитаем значение при котором заработает вторая
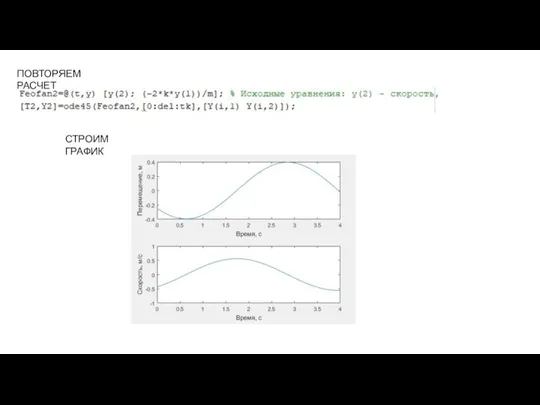
- 16. ПОВТОРЯЕМ РАСЧЕТ СТРОИМ ГРАФИК
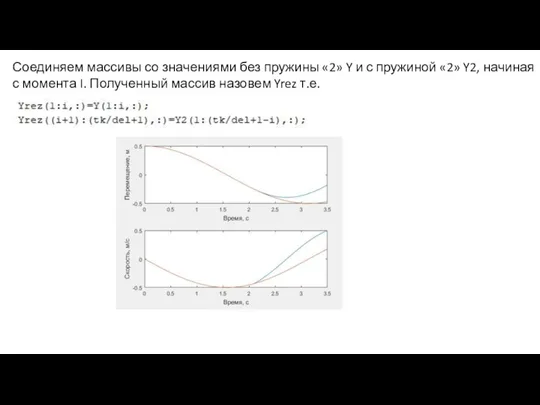
- 17. Соединяем массивы со значениями без пружины «2» Y и с пружиной «2» Y2, начиная с момента
- 18. Ну и наконец узнаем на сколько процентов уменьшится амплитуда при сжатии. Доделав свою работу суровый Феофан
- 20. Скачать презентацию











 Действие с дробями. Устная работа
Действие с дробями. Устная работа Тест 3 по математике
Тест 3 по математике Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа. Глава 1. Дифференциальное исчисление в нормированных пространствах Сфера и плоскость
Сфера и плоскость Диаграммы
Диаграммы Решение составных задач
Решение составных задач Пирамида Кукулькана – величайший храм майя
Пирамида Кукулькана – величайший храм майя Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой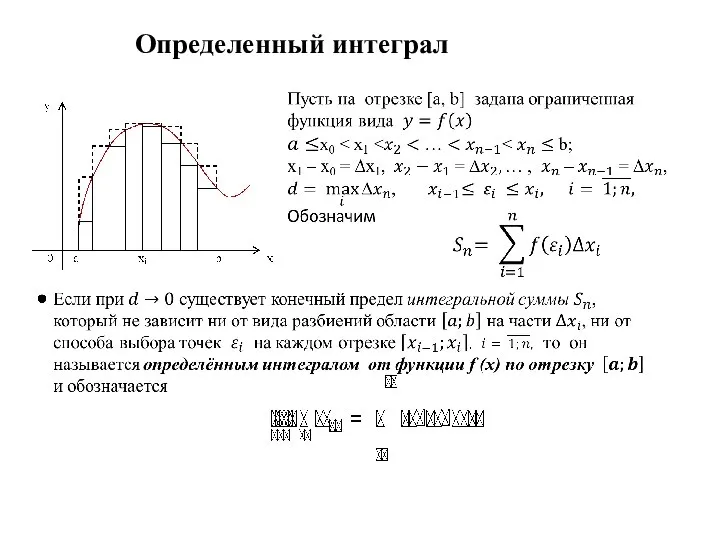 Определённый интеграл
Определённый интеграл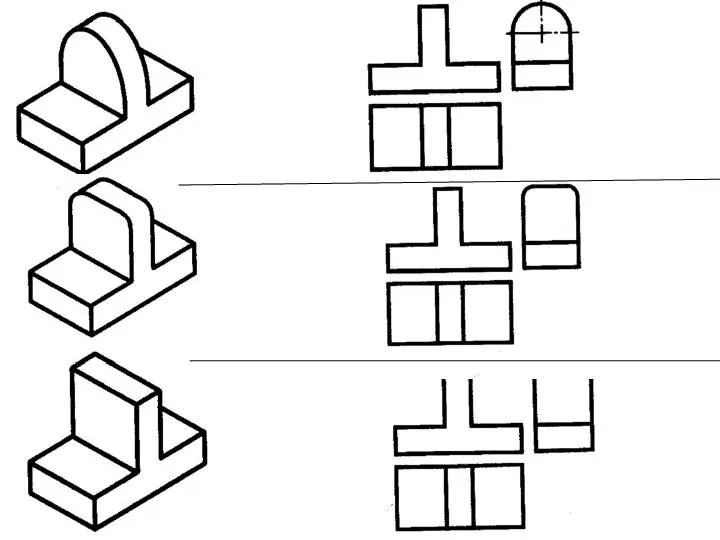 Проецирование на три взаимно перпендикулярные плоскости проекций
Проецирование на три взаимно перпендикулярные плоскости проекций Угол между прямыми
Угол между прямыми Porządki kompozycji symetria i asymetria
Porządki kompozycji symetria i asymetria Производная в экономике
Производная в экономике Цилиндр. Круговой цилиндр
Цилиндр. Круговой цилиндр Симметрия относительно прямой
Симметрия относительно прямой Презентация на тему Конусы в нашей жизни
Презентация на тему Конусы в нашей жизни  Математика в профессии геодезиста
Математика в профессии геодезиста Дидактический материал. Проверочные работы. Начальные понятия геометрии
Дидактический материал. Проверочные работы. Начальные понятия геометрии Аксиомы стереометрии
Аксиомы стереометрии Сумма углов треугольника
Сумма углов треугольника Определенный интеграл
Определенный интеграл Приближенные решения уравнений
Приближенные решения уравнений Определитель матрицы. Правило Крамера
Определитель матрицы. Правило Крамера Аналитическая панель
Аналитическая панель Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ 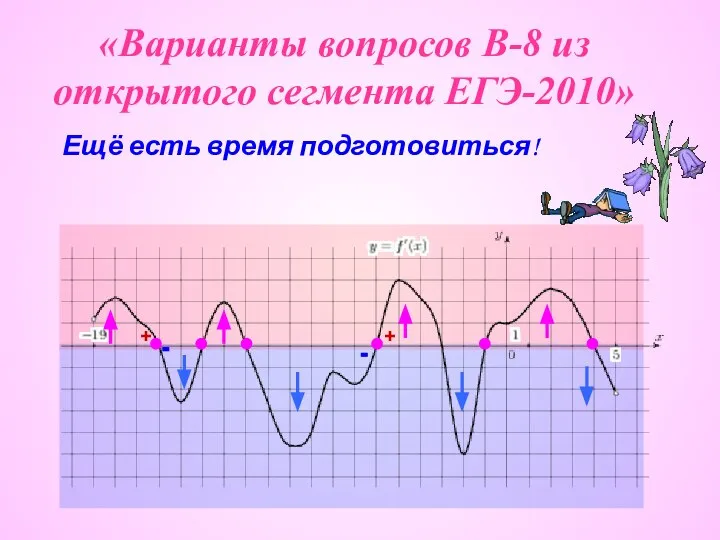 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Прогрессии в окружающей нас жизни
Прогрессии в окружающей нас жизни Подготовка к ЕГЭ В-4. Курс лекций по математике
Подготовка к ЕГЭ В-4. Курс лекций по математике