Описанная окружность. 8 класс

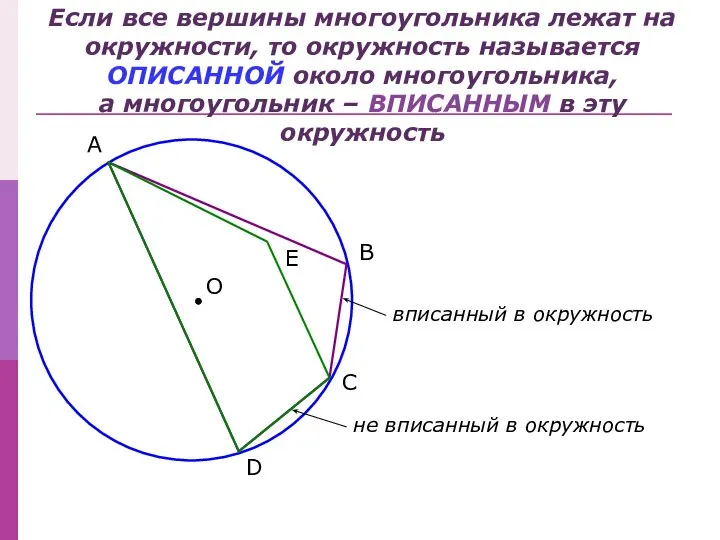
Если все вершины многоугольника лежат на окружности, то окружность называется
ОПИСАННОЙ около многоугольника,
а многоугольник – ВПИСАННЫМ в эту окружность
A
O
B
C
D
E
вписанный в окружность
не вписанный в окружность

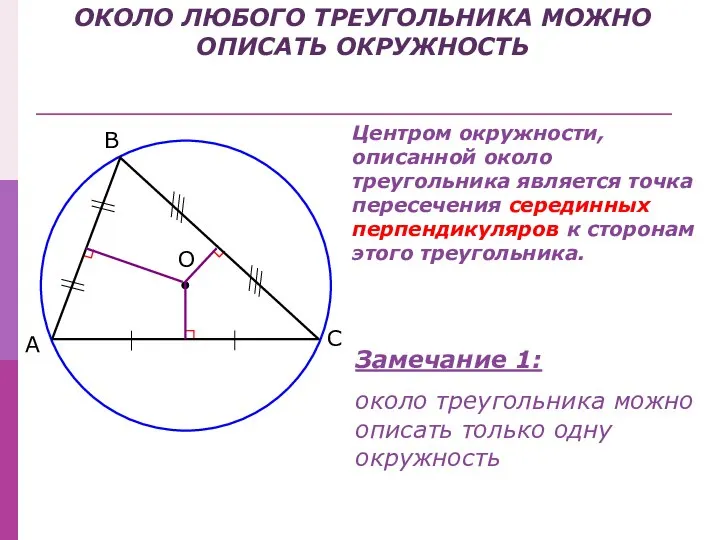
ОКОЛО ЛЮБОГО ТРЕУГОЛЬНИКА МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ
В
С
А
Замечание 1:
около треугольника можно описать только одну окружность
О
Центром окружности, описанной около треугольника является точка пересечения серединных перпендикуляров к сторонам этого треугольника.

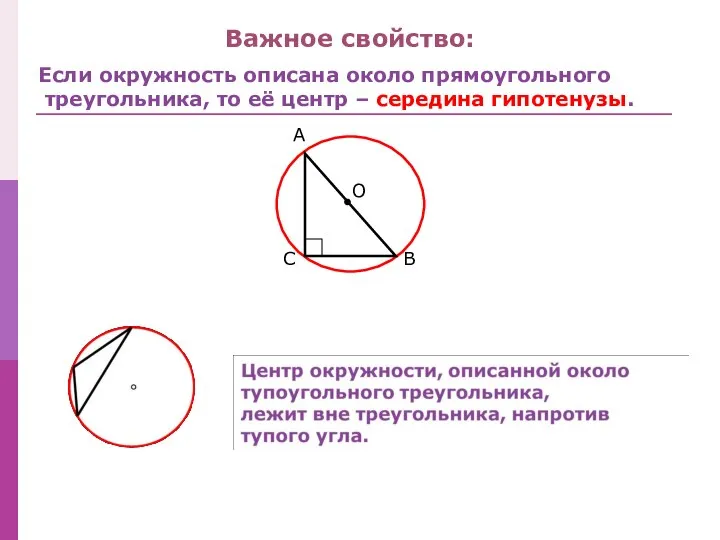
Важное свойство:
Если окружность описана около прямоугольного
треугольника, то её центр – середина гипотенузы.

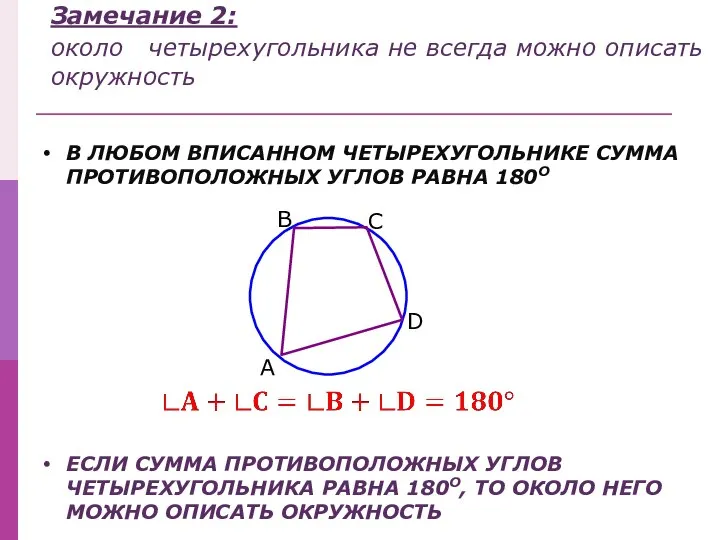
Замечание 2:
около четырехугольника не всегда можно описать окружность
В ЛЮБОМ ВПИСАННОМ ЧЕТЫРЕХУГОЛЬНИКЕ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ РАВНА 180О
ЕСЛИ СУММА ПРОТИВОПОЛОЖНЫХ УГЛОВ ЧЕТЫРЕХУГОЛЬНИКА РАВНА 180О, ТО ОКОЛО НЕГО МОЖНО ОПИСАТЬ ОКРУЖНОСТЬ
D
A
C
B

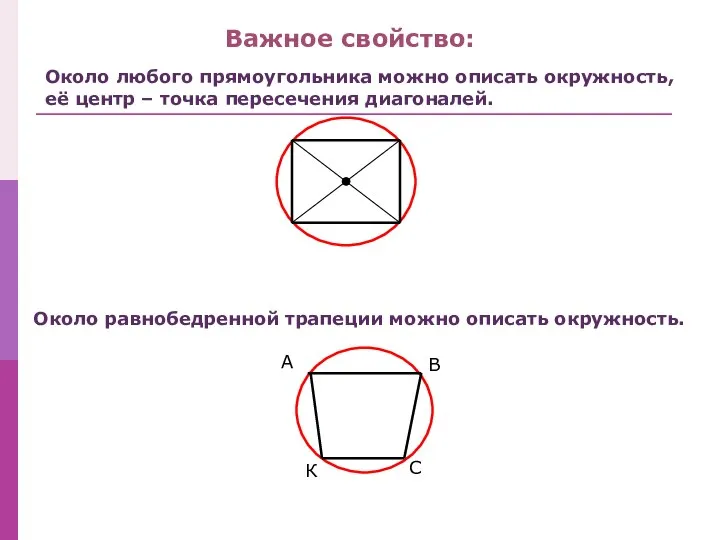
Около любого прямоугольника можно описать окружность, её центр – точка пересечения диагоналей.
Около равнобедренной трапеции можно описать окружность.
Важное свойство: