Содержание
- 2. Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π + t, π – t,
- 5. Любая из формул приведения может быть записана и для градусной меры угла, то есть когда под
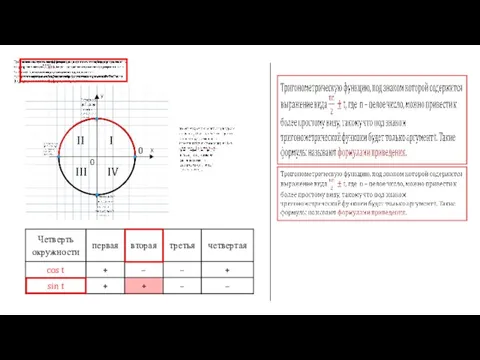
- 6. 0 I II III IV cos( π + t ) = – cos t Если под
- 7. 0 I II III IV
- 8. 0 I II III IV
- 9. 0 I II III IV Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π
- 10. Пример 1. Вычислить с помощью формул приведения sin ( –330° ). Решение. sin ( –t )
- 11. Пример 1. Вычислить с помощью формул приведения sin ( –330° ). Решение. sin ( –t )
- 12. Доказательство. ⟹ меняем наименование функции на cos;
- 13. Доказательство. ⟹ наименование функции сохраняем;
- 15. Скачать презентацию











 Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Наибольшее и наименьшее значение функций
Наибольшее и наименьшее значение функций Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц 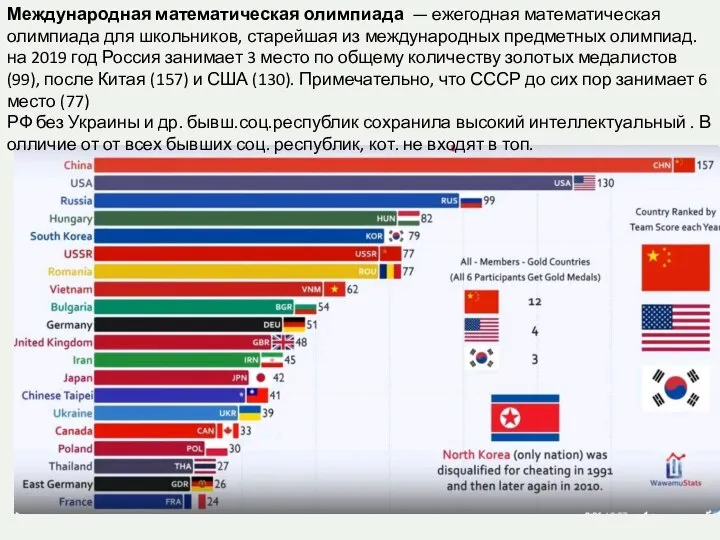 Международная математическая олимпиада
Международная математическая олимпиада Многоугольники в нашей жизни
Многоугольники в нашей жизни Формирование математических представлений, умений и навыков у дошкольников
Формирование математических представлений, умений и навыков у дошкольников Геометрический смысл производной. Производная и её геометрический смысл
Геометрический смысл производной. Производная и её геометрический смысл Согласные звуки [в],[ в’], буквы В, в
Согласные звуки [в],[ в’], буквы В, в Векторы в пространстве
Векторы в пространстве Пример записи решения задания к Части I РГР №1
Пример записи решения задания к Части I РГР №1 Презентация на тему Неопределенный интеграл
Презентация на тему Неопределенный интеграл  Статистический анализ случайных погрешностей
Статистический анализ случайных погрешностей Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Понятие области
Понятие области Проценты. 5 класс
Проценты. 5 класс Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Окружность и круг
Окружность и круг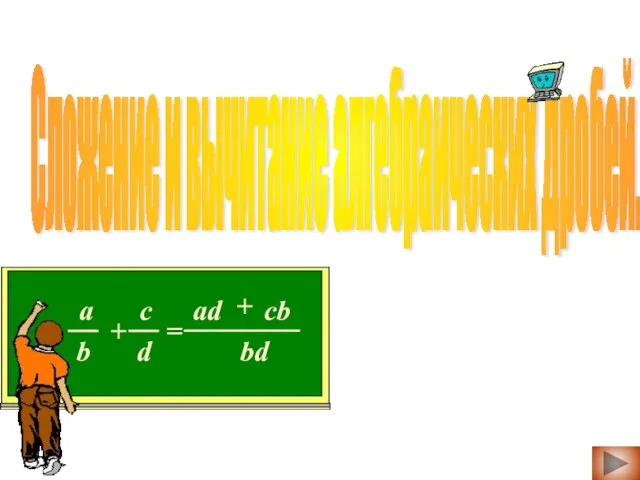 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Презентация на тему Формулы дифференцирования
Презентация на тему Формулы дифференцирования  Прибавить и вычесть 4
Прибавить и вычесть 4 Проценты. Устная работа
Проценты. Устная работа Реляционная алгебра
Реляционная алгебра Системы неравенств
Системы неравенств Задачи о зиме
Задачи о зиме Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Способы задания арифметической прогрессии
Способы задания арифметической прогрессии Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7
Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7