Содержание
- 2. Содержание Введение………………………………………………....3 Изучение курса………………………………….……11 Методика и особенности курса……………..13 Общая характеристика курса (логика построения курса)…………………………………..39 Программа курса(Примеры
- 3. Основная цель изучения курса «Математика и конструирование» состоит в том, чтобы обеспечить числовую грамотность учащихся, дать
- 4. Конструкторские умения включают в себя умения узнавать изученные геометрические фигуры в объектах, выделять их; умение составлять
- 5. В соответствии с изложенными целями обучения основными положениями содержания и структуры курса являются: преемственность с действующим
- 6. курсом трудового обучения, особенно в той его части, которая обеспечивает формирование трудовых умений и навыков работы
- 7. усиление геометрической линии начального курса математики, обеспечивающей развитие пространственных представлений и воображения учащихся и включающей в
- 8. усиление графической линии действующего курса трудового обучения, обеспечивающей умения изобразить на бумаге сконструированную модель и, наоборот,
- 9. привлечение дополнительного материала из математики и трудового обучения, который связан с идеей интеграции курса и обеспечивает
- 10. Курс «Математика и конструирование» даёт возможность дополнить учебный предмет «математика» практической конструкторской деятельностью учащихся.
- 11. Изучение курса предполагает органическое единство мыслительной и практической деятельности учащихся во всём многообразии их взаимного влияния
- 12. Специфика целей и содержания курса «Математика и конструирование» определяет и своеобразие методики его изучения, форм и
- 13. В методике проведения занятий по курсу «Математика и конструирование» учитываются возрастные особенности и возможности детей младшего
- 14. Изучение геометрического материала идёт на уровне представлений, а за основу изложения учебного материала берётся наглядность и
- 15. Элементы конструкторско-практической деятельности учеников равномерно распределяется за весь курс, и включаются в каждое занятие курса «Математика
- 16. Особое внимание в курсе уделяется рассмотрению формы и взаимного расположения геометрических фигур на плоскости и в
- 17. Работа по изготовлению моделей геометрических фигур и композиций из них сопровождается вычерчиванием промежуточных или конечных результатов,
- 18. В основе построения данного курса лежит идея гуманизации математического образования, соответствующая современным представлениям о целях школьного
- 19. Начальный курс математики объединяет арифметический, алгебраический и геометрический материалы. При этом вопросы геометрии затрагиваются очень поверхностно,
- 20. Предлагаемый курс предназначен для развития математических способностей учащихся, для формирования элементов логической и алгоритмической грамотности, коммуникативных
- 21. Содержание курса «Математика и конструирование» направлено на воспитание интереса к предмету, развитию наблюдательности, геометрической зоркости, умения
- 22. Ценностными ориентирами содержания данного курса являются: формирование умения рассуждать как компонента логической грамотности; освоение эвристических приемов
- 23. формирование способностей наблюдать, сравнивать, обобщать, находить простейшие закономерности, использовать догадку, строить и проверять простейшие гипотезы; формирование
- 24. Место курса в учебном плане. Содержание курса «Математика и конструирование» отвечает требованию к организации внеурочной деятельности:
- 25. Методы и приемы изучения материала. Одна из важных особенностей курса «Математика и конструирование» - его геометрическая
- 26. Одновременно с изучением арифметического материала и в органичном единстве с ним выстраивается система задач и заданий
- 27. Основой освоения геометрического содержания курса является конструкторско-практическая деятельность учащихся, включающая в себя: воспроизведение объектов; доконструирование объектов;
- 28. Большое внимание в курсе уделяется поэтапному формированию навыков самостоятельного выполнения заданий, самостоятельному получению свойств геометрических понятий,
- 29. В методике проведения занятий учитываются возрастные особенности детей младшего школьного возраста, и материал представляется в форме
- 30. При первоначальном введении основных геометрических понятий (точка, линия, плоскость) используются нестандартные способы: создание наглядного образа с
- 31. С целью освоения этих геометрических фигур выстраивается система специальных практических заданий, предполагающая изготовление моделей изучаемых геометрических
- 32. Для выполнения заданий такого характера используются счетные палочки, листы бумаги и картона, пластилин, мягкая проволока и
- 33. Так, после введения одной из важнейших линейных геометрических фигур – отрезка – предусмотрена целая серия специальных
- 34. Далее отрезки используются для изготовления силуэтов различных объектов, в том числе и каркасов геометрических фигур, как
- 35. В последнем случае предполагается обязательная фиксация (запись в числовом виде) проведенного действия. В практике выполнения заданий
- 36. Сначала выкладывают силуэты плоскостных объектов и фигур (модели цифр, букв, различных многоугольников), но постепенно уровень трудностей
- 37. Большое внимание в курсе уделяется развитию познавательных способностей. Термин познавательные способности понимается в курсе так, как
- 38. Основа развития познавательных способностей детей как сенсорных, так и интеллектуальных - целенаправленное развитие при обучении математике
- 39. Общая характеристика курса. Курс «Математика и конструирование» входит во внеурочную деятельность по направлению общеинтеллектуальное развитие личности.
- 40. В процессе выполнения заданий дети учатся видеть сходства и различия, замечать изменения, выявлять причины и характер
- 41. Программа учитывает возрастные особенности младших школьников и поэтому предусматривает организацию подвижной деятельности учащихся, которая не мешает
- 42. Во время занятий важно поддерживать прямое общение между детьми (возможность подходить друг к другу, переговариваться, обмениваться
- 43. Первый год обучения ставит цель- научить ориентироваться в таких понятиях «влево», «вправо», «вверх», «вниз», проводить задания
- 44. Второй год обучения ставит цели - сформировать у учащихся основные базовые понятия, такие как: «точка», «линия»,
- 45. Третий год обучения ставит целью дополнить и расширить знания учащихся, полученные ранее. Программой предусмотрено знакомить с
- 46. Четвертый год ставит цели знакомить учащихся с понятием высота, медиана, биссектриса, их построениями: определять площади геометрических
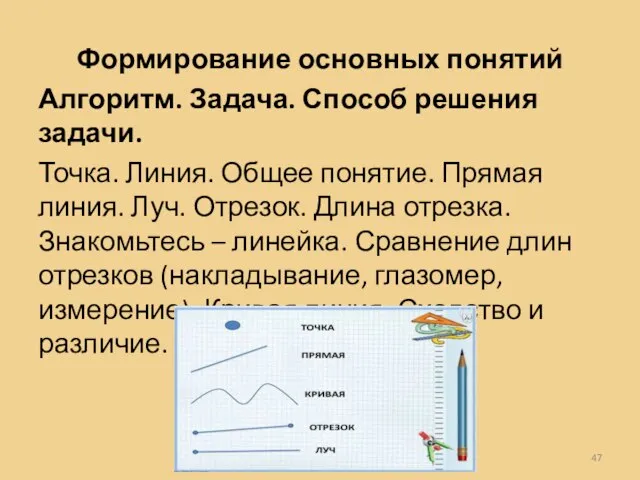
- 47. Формирование основных понятий Алгоритм. Задача. Способ решения задачи. Точка. Линия. Общее понятие. Прямая линия. Луч. Отрезок.
- 48. Углы. Луч. Угол. Вершина угла. Плоскость. Перпендикуляр. Прямой угол. Угольник. Прямой, острый, тупой углы. Развернутый угол.
- 49. Треугольники. Треугольник. Вершины. Стороны. Прямоугольный треугольник. Тупоугольный треугольник. Остроугольный треугольник. Равносторонний треугольник. Сравнение треугольников. Из множества
- 50. Четырехугольники. Четырехугольники. Вершины. Стороны. Диагонали. Квадрат. Построение квадратов и его диагоналей на линованной и нелинованной бумаге.
- 51. Программа курса «Математика и конструирование»
- 52. 1 класс Формировать умения ориентироваться в пространственных понятиях «влево», «вправо», «вверх», «вниз» и т.д., проводить задания
- 53. Мир занимательных задач Задачи, допускающие несколько способов решения. Задачи с недостаточными, некорректными данными, с избыточным составом
- 54. Задачи на доказательство, например, найти цифровое значение букв в условной записи: СМЕХ + ГРОМ = ГРЕМИ
- 55. Пример упражнения для 1 класса
- 57. 2 класс. Формирование основных понятий: точка, линия, прямая линия, отрезок, длина отрезка, линейка, луч, построение луча,
- 58. Пример упражнений для 2 класса
- 61. 3 класс. Символика. Построение. Обозначение буквами точек, отрезков, линий, лучей, вершин углов. Латинский алфавит. Прямая линия.
- 62. Пример упражнения для 3 класса
- 64. 4 класс. Высота. Медиана. Биссектриса. Треугольники, высота, медиана, биссектриса основание и их построение. Прямоугольный треугольник. Катет
- 65. Геометрическая фигура. Геометрическое тело. Понятие объема. Геометрическое тело. Квадрат и куб. Сходство и различие. Построение пирамиды.
- 66. Примеры упражнений для 4 класса
- 68. Основные требования к знаниям, умениям и навыкам учащихся: 1. К концу 1 класса учащиеся должны уметь
- 69. 2. К концу 2 класса учащиеся должны знать термины: точка, прямая, отрезок, угол, ломаная, треугольник, прямоугольник,
- 70. 3. К концу 3 класса учащиеся должны владеть терминами, изученными во втором классе. Также учащиеся должны
- 71. 4. К концу 4 класса учащиеся должны владеть терминами: высота, медиана, биссектриса, основание, прямоугольный треугольник, катет,
- 72. Универсальные учебные действия Сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания. Моделировать в
- 74. Скачать презентацию






































































 Решение задач к главе IV §1,2
Решение задач к главе IV §1,2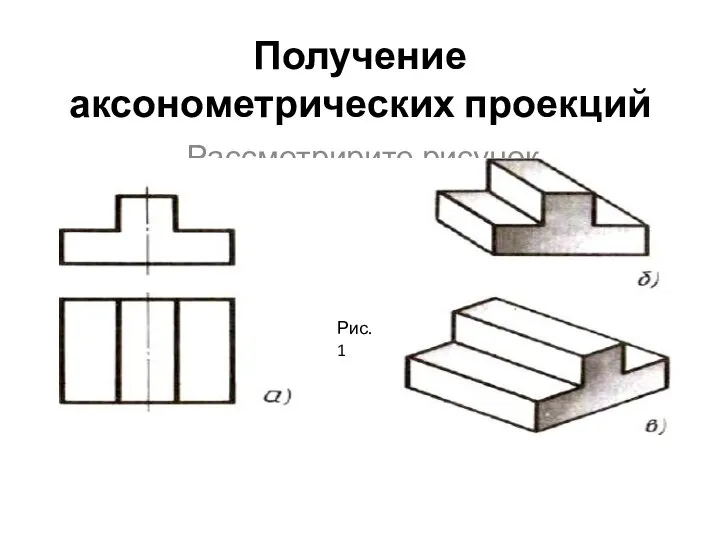 Получение аксонометрических проекций
Получение аксонометрических проекций Лекция_04
Лекция_04 Задачи по теме: Смеси и сплавы. Подготовка к ЕГЭ. Профильный уровень. №11
Задачи по теме: Смеси и сплавы. Подготовка к ЕГЭ. Профильный уровень. №11 Решение систем линейных уравнений методом сложения
Решение систем линейных уравнений методом сложения Брейн-ринг. Геометрия
Брейн-ринг. Геометрия Линейные пространства и линейные операторы. Лекция 6
Линейные пространства и линейные операторы. Лекция 6 Движение
Движение Решение текстовых задач с помощью уравнений
Решение текстовых задач с помощью уравнений Умножение. Законы умножения
Умножение. Законы умножения Полимино
Полимино Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Правила построения алгоритма
Правила построения алгоритма Вероятность и статистика
Вероятность и статистика Определение арифметической прогрессии
Определение арифметической прогрессии Натуральные и целые числа
Натуральные и целые числа Презентация по математике "Свойства величин" -
Презентация по математике "Свойства величин" -  Объем прямой призмы
Объем прямой призмы Решение задач на проценты. Уравнения
Решение задач на проценты. Уравнения Число 10
Число 10 Системы неравенств с одной переменной
Системы неравенств с одной переменной Скалярное произведение векторов. тест
Скалярное произведение векторов. тест Фрактальное изображение
Фрактальное изображение Презентация на тему НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ
Презентация на тему НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ С НИМИ  SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY Решение уравнений
Решение уравнений Вычисление предела
Вычисление предела