Содержание
- 2. Устная работа Арифметическая прогрессия 1) 1, 3, 5, 7, 9, … d = 2 2) 5,
- 3. Определение Арифметической Геометрической прогрессией а1,а2,а3,…аn,.. b1,b2,b3,…bn,… называется последовательность, отличных от нуля чисел каждый член которой, начиная
- 4. Определение Числовая последовательность а1,а2,а3,…аn,.. b1,b2,b3,…bn,… называется арифметической геометрической если для всех натуральных n выполняется равенство an+1=
- 5. Вывод d>0 арифметическая прогрессия возрастающая d арифметическая прогрессия убывающая q > 1 геометрическая прогрессия возрастающая 0
- 6. Определите вид прогрессии В третьем тысячелетии високосными годами будут 2008, 2012 ,2016, 2020. В какой последовательности
- 7. Формула n-го члена прогрессии Пусть заданы а1 и d а2=а1+d a3=a2+d=a1+d+d=а1+2d a4=a3+d=а1+3d …………………………….. an=a1+(n-1)d Пусть заданы
- 8. Составьте геометрическую прогрессию: Ежедневно каждый болеющий ковидом может заразить четырех окружающих. 1; 4; 16; 64;… Дима
- 9. Работа в тетрадях Задание 1. Дано: (bn ) - геометрическая прогрессия b1= 5 q = 3
- 10. Работа в тетрадях Задание 2. Дано: (bn ) - геометрическая прогрессия b4= 40 q = 2
- 11. Работа в тетрадях Задание 3. Дано: (bn ) - геометрическая прогрессия b1= -2, b4=-54. Найти: q.
- 12. Биология Каждое простейшее одноклеточное животное инфузория туфелька размножается делением на 2 части. Сколько инфузорий было первоначально,
- 13. Заданы три первых члена числовых последовательностей. Известно, что одна из этих последовательностей не является геометрической прогрессией.
- 14. Последовательности (an), (bn), (cn) заданы формулами n-го члена. Поставьте в соответствие каждой последовательности верное утверждение. ФОРМУЛА
- 16. Скачать презентацию













 Центральная симметрия
Центральная симметрия Логарифмические уравнения
Логарифмические уравнения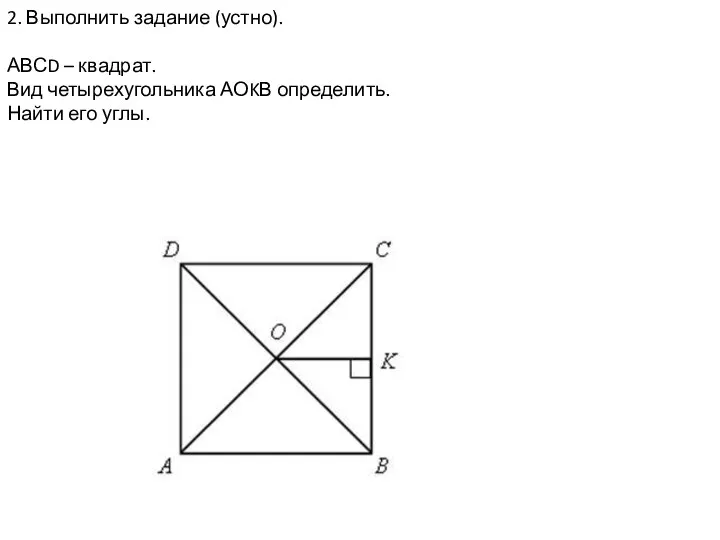 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Признак существования определенного интеграла. Лекция №7
Признак существования определенного интеграла. Лекция №7 Дифференциальные уравнения I порядка с разделяющимися переменными
Дифференциальные уравнения I порядка с разделяющимися переменными Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем
Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы
Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел Логика. Введение
Логика. Введение Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Занимательная математика. 2 класс
Занимательная математика. 2 класс Презентация на тему РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ
Презентация на тему РАЗЛОЖЕНИЕ НА ПРОСТЫЕ МНОЖИТЕЛИ  Комплексные числа и действия над ними
Комплексные числа и действия над ними Умножение натуральных чисел 5 класс
Умножение натуральных чисел 5 класс Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс) 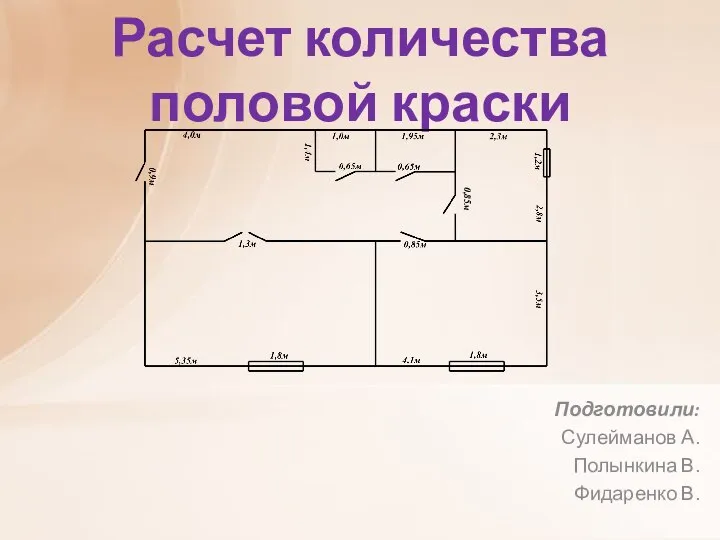 Расчет количества половой краски
Расчет количества половой краски Классическое определение вероятности
Классическое определение вероятности Длина окружности. Площадь круга
Длина окружности. Площадь круга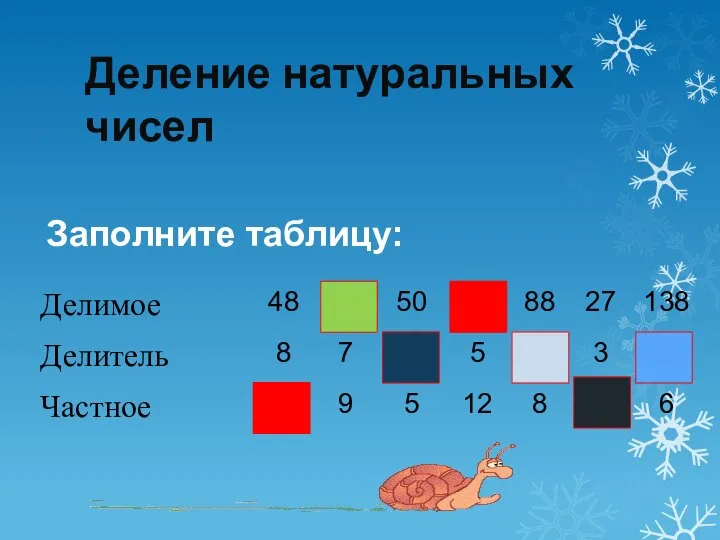 Деление натуральных чисел
Деление натуральных чисел Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики
Педагогические приемы включения детей, имеющих нарушения слуха, в образовательное пространство урока математики Презентация на тему Разность квадратов
Презентация на тему Разность квадратов  Дроби вокруг нас
Дроби вокруг нас Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Алгебра логики
Алгебра логики Линейные операции над векторами
Линейные операции над векторами Анализ контрольной работы
Анализ контрольной работы