Содержание
- 2. Если все исходы какого-либо испытания равновозможные, то вероятность события в этом испытании равна отношению числа благоприятных
- 3. Какова вероятность того, что при броске игрального кубика выпадает 2 или 3? В коробке находятся 20
- 4. ЗАДАЧА №1 На карточках написаны номера от 4 до 35. Какова вероятность того, что случайно выбранная
- 5. ЗАДАЧА №2 Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми
- 6. ЗАДАЧА №4 Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом
- 7. РЕШЕНИЕ. ЗАДАЧА №5 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих
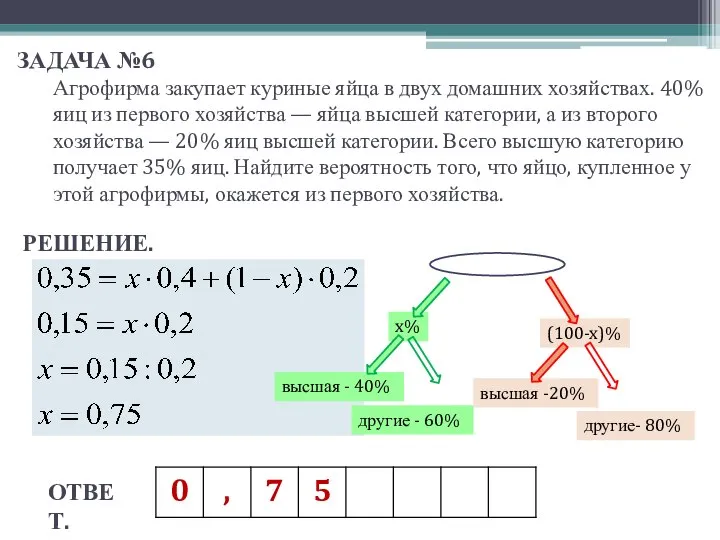
- 8. РЕШЕНИЕ. ЗАДАЧА №6 Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства
- 9. РЕШЕНИЕ. ЗАДАЧА №7 На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и
- 11. Скачать презентацию







 Многогранники и их основные свойства
Многогранники и их основные свойства Формула сложных процентов в ЕГЭ. 11 класс
Формула сложных процентов в ЕГЭ. 11 класс Сокращенное умножение многочленов
Сокращенное умножение многочленов Переместительный и сочетательный законы сложения
Переместительный и сочетательный законы сложения Практика. Дискретная математика
Практика. Дискретная математика Презентация на тему Софья Васильевна Ковалевская
Презентация на тему Софья Васильевна Ковалевская  Уравнение прямой
Уравнение прямой Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Координаты вектора
Координаты вектора Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Миллиметр. В каких числах сумма цифр равна 5?
Миллиметр. В каких числах сумма цифр равна 5?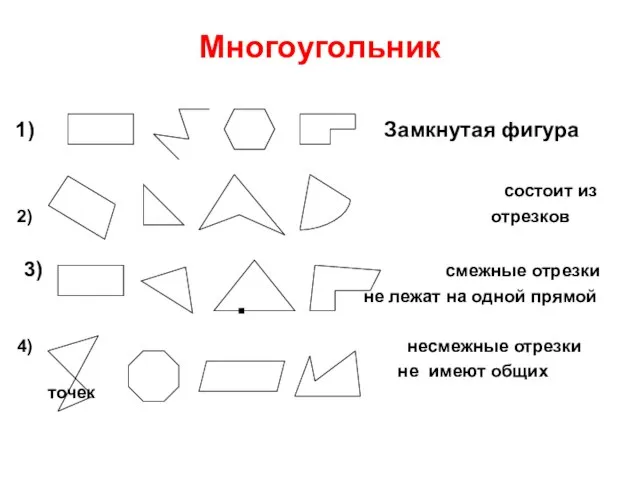 Классификация многоугольников по числу углов
Классификация многоугольников по числу углов Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Презентация на тему Развивающие задачи для 5-6 классов
Презентация на тему Развивающие задачи для 5-6 классов  Переместительное свойство умножения
Переместительное свойство умножения Свойства умножения. 5 класс
Свойства умножения. 5 класс Математический турнир Умники и умницы
Математический турнир Умники и умницы Исследование операций. Принятие решений и неопределенность. Лекция 3
Исследование операций. Принятие решений и неопределенность. Лекция 3 11 клас призма
11 клас призма Метод Гаусса решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений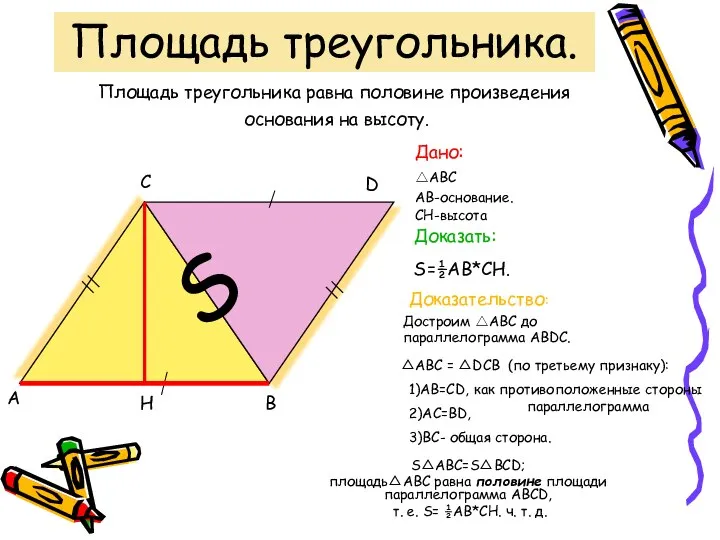 Площадь треугольника
Площадь треугольника Параллельные прямые
Параллельные прямые Презентация на тему Построение точек по заданным координатам
Презентация на тему Построение точек по заданным координатам  Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Состав чисел в приделах 10. Закрепление изученного материала
Состав чисел в приделах 10. Закрепление изученного материала Корень n-ой степени
Корень n-ой степени Шестое математическое действие
Шестое математическое действие Подготовка к ЕГЭ. Тестирование
Подготовка к ЕГЭ. Тестирование