Содержание
- 2. ПОЛЕЗНАЯ ИНФОРМАЦИЯ Перед тобой темы курса Алгебры 8 класса. *чтобы открыть более детальную информацию следует нажать
- 3. ПОЛЕЗНАЯ ИНФОРМАЦИЯ Перед тобой три эвристических приёма, они применяются при решении задач по теме «Квадратные уравнения».
- 4. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 5. Это эвристический прием, используемый в алгебре для формоизменения текста задачи. Его суть заключается в следующем. Если
- 6. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 7. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 8. Это эвристический прием решения многих алгебраических задач: решение днофантовых выражений, нахождение наибольших и наименьших значение функции,
- 9. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 10. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 11. Прием используется при решении заданий, условия которых сформулированы в виде неопределенности типа "Правильно ли …?", "Существует
- 12. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 13. ПОЛЕЗНАЯ ИНФОРМАЦИЯ Перед тобой три эвристических приёма, они применяются при решении задач по теме «Квадратные уравнения».
- 14. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 15. Прием используется при решении заданий, условия которых сформулированы в виде неопределенности типа "Правильно ли …?", "Существует
- 16. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 17. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 18. Особенность этого приема состоит в переходе к равносильной задаче, чаще всего алгоритмической, путем перевода текста исходной
- 19. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 20. ПОЛЕЗНАЯ ИНФОРМАЦИЯ Перед тобой три эвристических приёма, они применяются при решении задач по теме «Квадратные уравнения».
- 21. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 22. Особенность этого приема состоит в переходе к равносильной задаче, чаще всего алгоритмической, путем перевода текста исходной
- 23. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 24. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 25. Прием используется для восстановления того или иного выражения по какой-либо его части, если это выражение совпадает
- 26. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 27. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
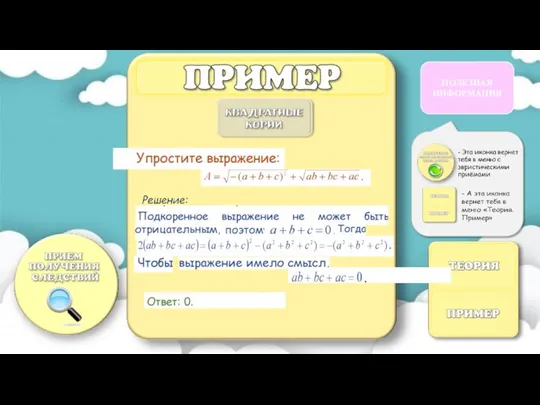
- 28. Прием состоит в том, что раскрытие содержания исходных данных дает возможность получить некоторые выводы, а из
- 29. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 30. ПОЛЕЗНАЯ ИНФОРМАЦИЯ Перед тобой три эвристических приёма, они применяются при решении задач по теме «Квадратные уравнения».
- 31. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 32. Чтобы показать истинность утверждения , достаточно указать хотя бы одно значение х из Х, для которого
- 33. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 34. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 35. Достаточно универсальный эвристический прием, смысл которого заключается в том, чтобы найти такие «составляющие» данного объекта (выражения,
- 36. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
- 37. ПОЛЕЗНАЯ ИНФОРМАЦИЯ
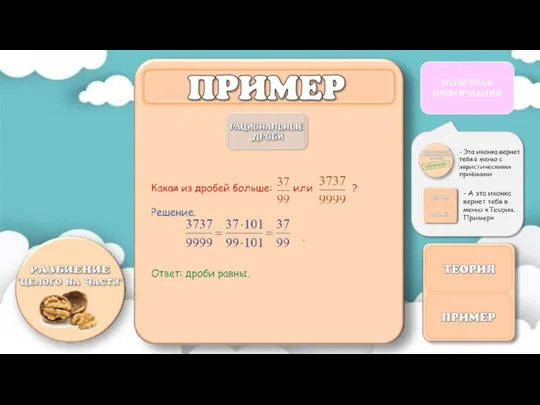
- 38. Отыскиванию конкретных способов решения целого ряда задач, условия которых содержат дробно-рациональные выражения, помогает прием выделения целой
- 40. Скачать презентацию

































 Построение призмы с вырезом
Построение призмы с вырезом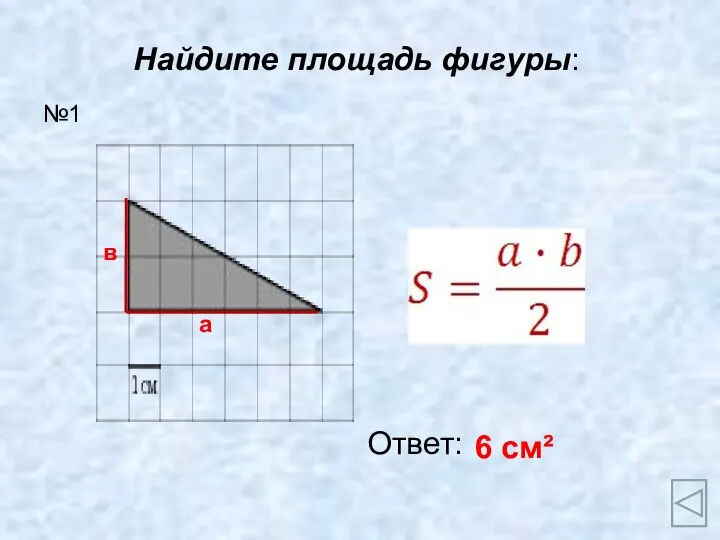 Формулы площадей
Формулы площадей Корни натуральной степени из числа и их свойства
Корни натуральной степени из числа и их свойства Значение степени возведение в степень
Значение степени возведение в степень Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Производная функции. Решения
Производная функции. Решения Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Разложение вектора по трем некомпланарным векторам
Разложение вектора по трем некомпланарным векторам Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Правильный восьмиугольник
Правильный восьмиугольник Арифметические действия
Арифметические действия Кратные криволинейные и поверхностные интегралы
Кратные криволинейные и поверхностные интегралы Объем наклонной призмы. Теорема
Объем наклонной призмы. Теорема Возведение в степень
Возведение в степень Координаты вектора. Простейшие задачи в координатах
Координаты вектора. Простейшие задачи в координатах Метрология. Лекция 1
Метрология. Лекция 1 Ломанная линия
Ломанная линия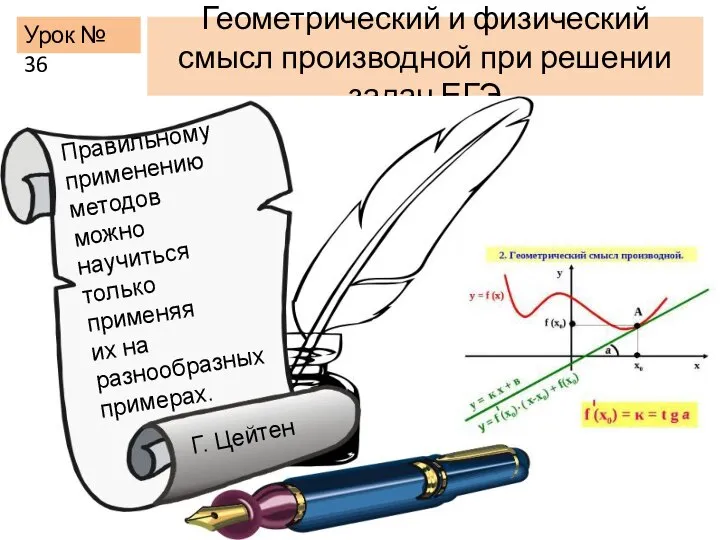 Геометрический и физический смысл производной при решении задач ЕГЭ
Геометрический и физический смысл производной при решении задач ЕГЭ Интервальные оценки
Интервальные оценки Метрология. Основные понятия
Метрология. Основные понятия Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Дифференциальные уравнения
Дифференциальные уравнения Площа паралелограма
Площа паралелограма Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Логарифмическая спираль
Логарифмическая спираль Решение прямоугольных треугольников
Решение прямоугольных треугольников Кубические см
Кубические см Геометрия. Это полезно знать
Геометрия. Это полезно знать