Содержание
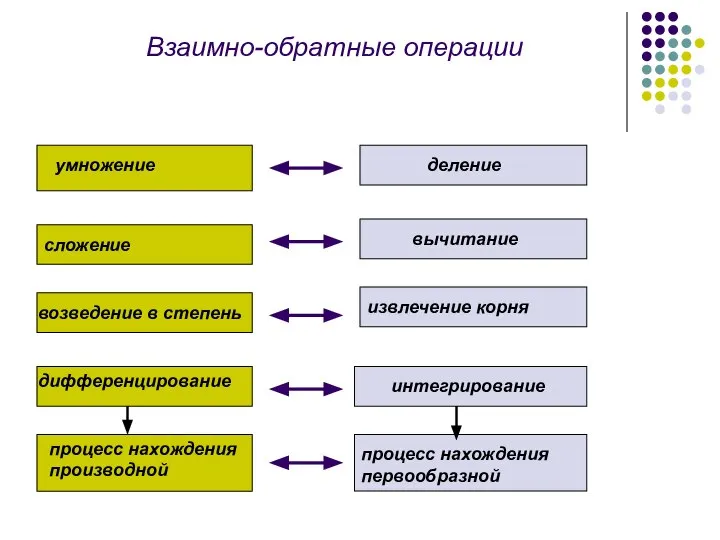
- 2. умножение деление сложение вычитание возведение в степень извлечение корня дифференцирование интегрирование Взаимно-обратные операции процесс нахождения производной
- 3. Первообразной для функции f(x) называется функция, производная которой равна данной Определение первообразной Функция F(x) называется первообразной
- 4. Таблица первообразных некоторых функций
- 5. Найти первообразную функций
- 6. Найти производную функции F(x): 1 ряд 2 ряд 3 ряд Вывод: для данной функции существует множество
- 7. Таблица первообразных некоторых функций
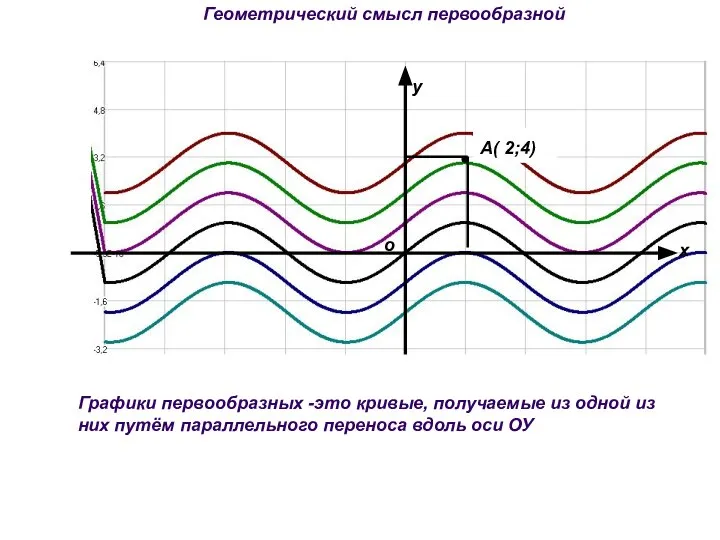
- 8. Геометрический смысл первообразной Графики первообразных -это кривые, получаемые из одной из них путём параллельного переноса вдоль
- 10. Скачать презентацию





 Звёздчатые многогранники
Звёздчатые многогранники Число и цифра 6
Число и цифра 6 Обратная матрица
Обратная матрица Приёмы сложения однозначных чисел с переходом через десяток
Приёмы сложения однозначных чисел с переходом через десяток Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Презентация на тему Виды треугольников
Презентация на тему Виды треугольников  Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Прямое сложение и вычитание
Прямое сложение и вычитание Статистическая обработка массива однородных величин. Практическое занятие 2
Статистическая обработка массива однородных величин. Практическое занятие 2 Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Виды треугольников по углам
Виды треугольников по углам Эварист Галуа
Эварист Галуа Элементы комбинаторики
Элементы комбинаторики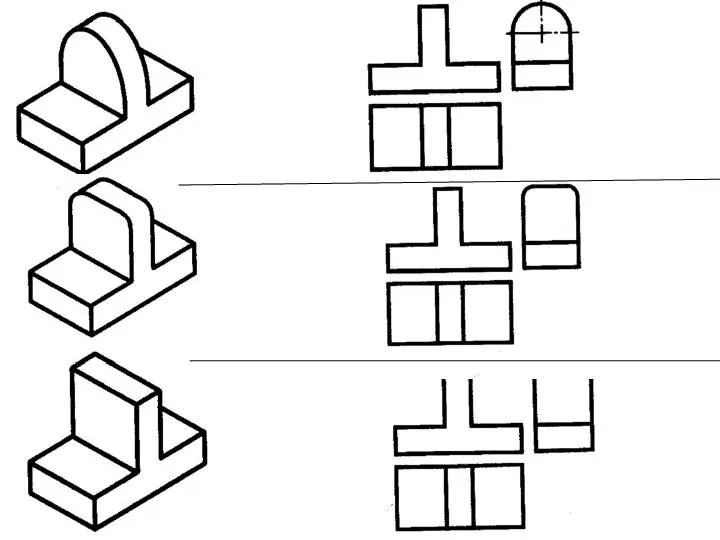 Проецирование на три взаимно перпендикулярные плоскости проекций
Проецирование на три взаимно перпендикулярные плоскости проекций Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ Математические методы в филологии
Математические методы в филологии Теоремы Менелая и Чевы
Теоремы Менелая и Чевы Кратные интегралы
Кратные интегралы Многогранники
Многогранники Одночлены. Обобщающий урок
Одночлены. Обобщающий урок Второй признак равенства треугольников. Геометрия , 7 класс
Второй признак равенства треугольников. Геометрия , 7 класс Задачи на части
Задачи на части Криволинейные интегралы
Криволинейные интегралы Математика 1 класс
Математика 1 класс Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Наибольшее и наименьшее значение функции на отрезке
Наибольшее и наименьшее значение функции на отрезке