Ошибки результатов измерений

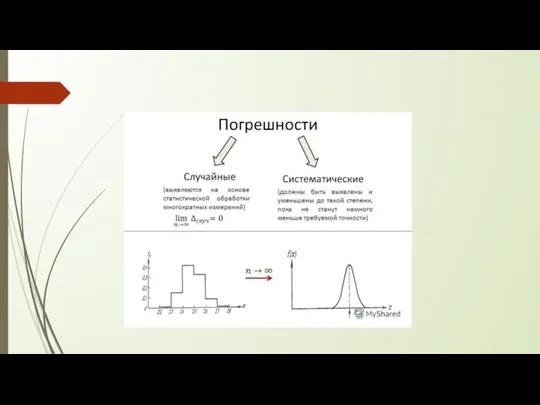
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного. Это отклонение принято называть ошибкой измерения. (В ряде источников, например в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно рекомендации РМГ 29-99 термин ошибка измерения не рекомендуется применять как менее удачный, а РМГ 29-2013 его вообще не упоминает[1]). Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют действительное значение величины хд, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него[1]. Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T = 2,8 ± 0,1 с означает, что истинное значение величины T лежит в интервале от 2,7 с до 2,9 с с некоторой оговорённой вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка, предел погрешности).

«Классификация ошибок результатов измерений»
Случайные ошибки
Систематические ошибки
Элементарные ошибки
Ошибки объекта измерений
Личные ошибки
Приборные ошибки
Ошибки метода
Внешние ошибки

Случайные ошибки вызываются большим числом отдельных причин, действующих в каждом отдельном измерении различными способами. В примере со взвешиванием это могут быть незаметные глазу колебания чаши весов, потоки воздуха, толчки фундамента здания, в котором стоят весы. Эти ошибки полностью исключить невозможно.

Систематические ошибки обуславливаются причинами, действующими вполне определенным образом. Примером систематической ошибки при взвешивании может являться смещение стрелки ненагруженных весов относительно нулевой отметки на некоторую постоянную величину. Зная это смещение ( например, взвесив гирю, масса которой точно не известна), можно, всякий раз измеряя массу на этих весах, вычитать постоянную величину из показаний прибора. Таким образом, систематические ошибки могут быть устранены или достаточно точно учтены.