Содержание
- 2. ЦЕЛИ УРОКА: Дать определение средней линии треугольника. Доказать теорему о средней линии треугольника. Решать задачи, используя
- 3. Определение: Отрезок, соединяющий середины двух сторон треугольника, называют средней линией треугольника.
- 4. ТЕОРЕМА Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. B Доказательство:
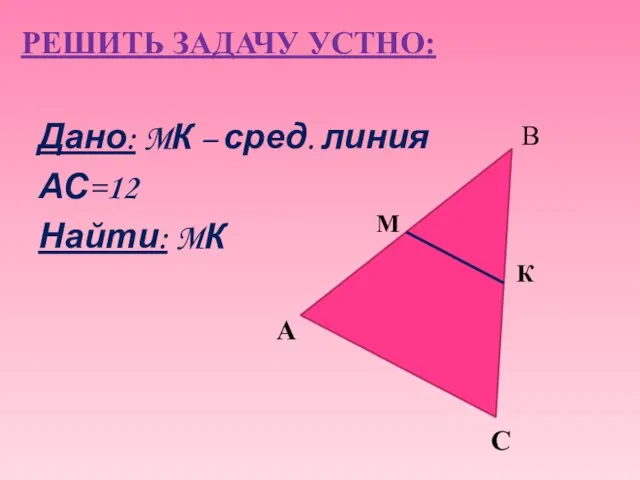
- 6. РЕШИТЬ ЗАДАЧУ УСТНО: Дано: MК – сред. линия АС=12 Найти: MК А К М С В
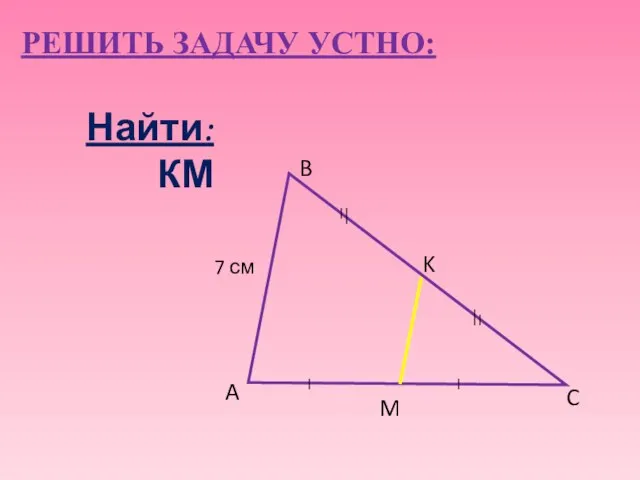
- 7. 7 см A B C M K РЕШИТЬ ЗАДАЧУ УСТНО: Найти: КМ
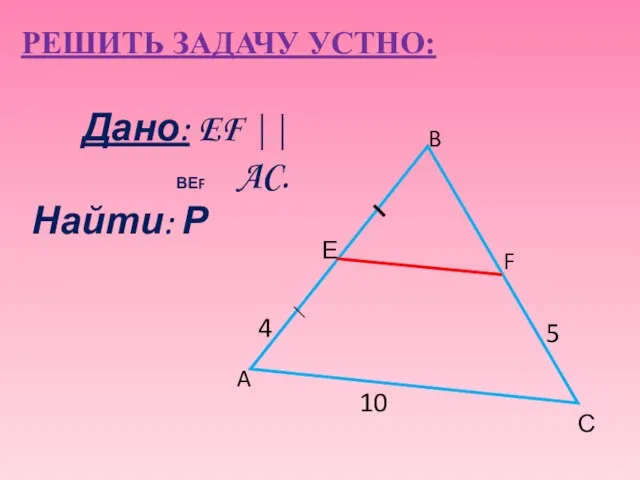
- 8. РЕШИТЬ ЗАДАЧУ УСТНО: Дано: EF || AC. Найти: Р 5 A B F Е 10 4
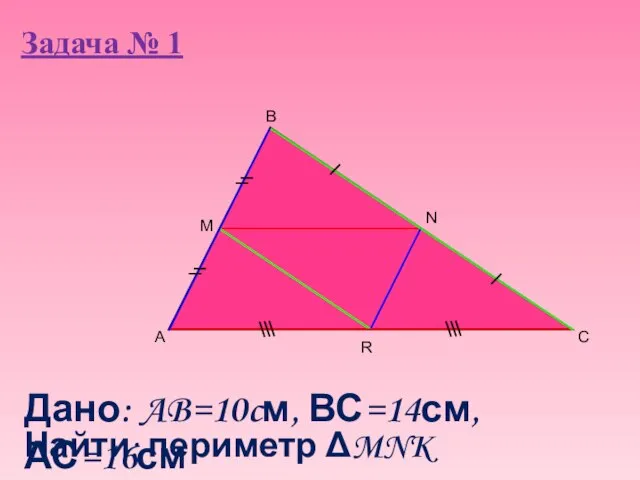
- 9. Задача № 1 A B C M Дано: AB=10cм, ВС=14см, АС=16см Найти: периметр ΔMNK R N
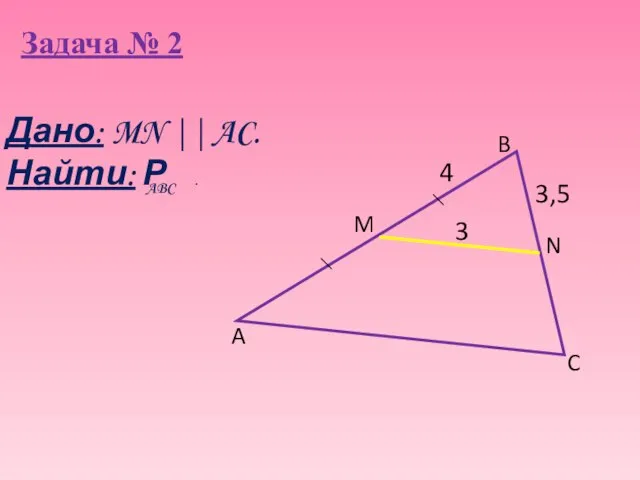
- 10. Задача № 2 3,5 A B C N M 3 4 Дано: MN || AC. Найти:
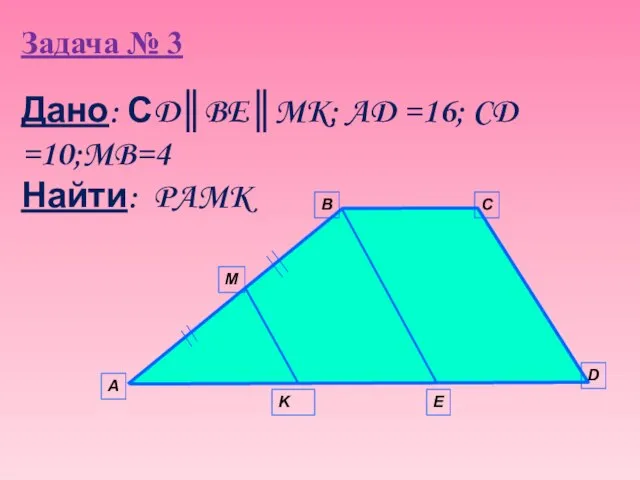
- 11. Задача № 3 А B C D E K M Дано: СD║BE║MK; AD =16; CD =10;MB=4
- 12. Какие новые знания получены на уроке? Что называют средней линией треугольника? Сформулируйте теорему о средней линии
- 14. Скачать презентацию





 Логика - это русло мысли
Логика - это русло мысли Тригонометрия. Контрольная работа
Тригонометрия. Контрольная работа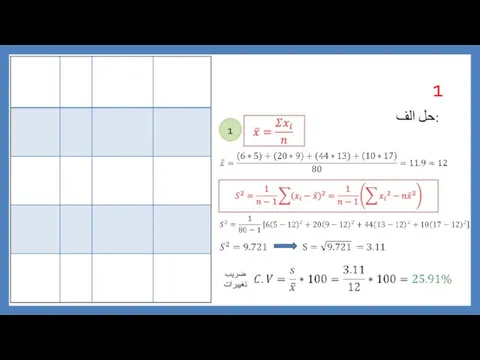 حل تمرین آمار
حل تمرین آمار Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Элементы комбинаторики
Элементы комбинаторики Решение алгебраических и трансцендентных уравнений
Решение алгебраических и трансцендентных уравнений Графики функций. Задания
Графики функций. Задания Методы общения линейных уравнений с тремя неизвестными
Методы общения линейных уравнений с тремя неизвестными Тригонометрически уравнения
Тригонометрически уравнения Углы треугольника
Углы треугольника Задачи на концентрацию
Задачи на концентрацию Задачи на готовых чертежах
Задачи на готовых чертежах Метод интервалов. Общий метод интервалов
Метод интервалов. Общий метод интервалов Смешаное число
Смешаное число Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс
Невыпуклый многогранник: Геометрическая фигура или плод человеческой фантазии? 11 класс Параллельность в пространстве
Параллельность в пространстве Теорема Муавра-Лапласа
Теорема Муавра-Лапласа Стороны прямоугольника. Задачи
Стороны прямоугольника. Задачи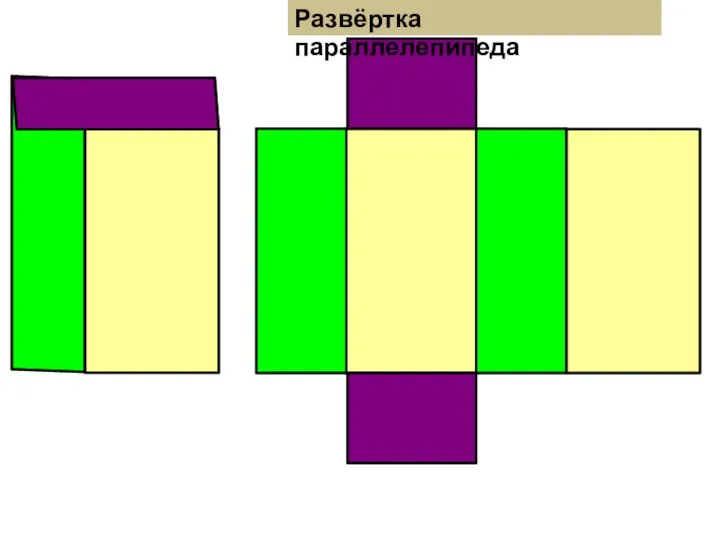 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ
Презентация на тему НАХОЖДЕНИЕ СУММЫ НЕСКОЛЬКИХ СЛАГАЕМЫХ  Применение технологий Веб 2.0 на уроках математики
Применение технологий Веб 2.0 на уроках математики Презентация на тему Скалярное произведение векторов (9 класс)
Презентация на тему Скалярное произведение векторов (9 класс)  Элементы комбинаторики
Элементы комбинаторики Уравнения
Уравнения Треугольники. Практика. Первый уровень
Треугольники. Практика. Первый уровень Задачи на построение
Задачи на построение Реши примеры устно. 2 класс
Реши примеры устно. 2 класс