Содержание
- 2. Вставьте заголовок слайда
- 3. ПОНЯТИЕ СРЕДНЕЙ ВЕЛИЧЕНЫ x СРЕДНЯЯ ВЕЛИЧИНА В СТАТИСТИКЕ-ОБОБЩАЮЩИЙ ПОКАЗАТЕЛЬ,ХАРАКТЕРИЗУЮЩИЙ ТИПИЧНЫЙ УРОВЕНЬ ЯВЛЕНИЯ,СВОДНАЯ ХАРАКТЕРИСТИКА ЗАКОНОМЕРНОСТЕЙ ТОГО ПРОЦЕССА,В
- 4. Средние величины...
- 5. Определяющее свойство средней Исходное соотношение ИСС: ИСС= Суммарное значение осредняемого показателя Количество единиц совокупности (объём)
- 6. ИСС ДЛЯ НЕКОТОРЫХ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
- 7. Средняя арифметическая (простая, взвешенная, средняя из групповых средних); Средняя гармоническая; Средняя геометрическая; Средняя степенная (квадратическая, кубическая
- 8. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЕЛИЧИНА Используется для расчёта среднего значения признака при известном объёме совокупности
- 9. Средняя арифметическая простая Используется для расчёта среднего значения признака при известных индивидуальных значениях признака (для несгруппированных
- 10. Средняя арифметическая взвешенная Вычисляется, если имеются многократные повторения значения признака и совокупность разбита на группы, используется
- 11. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ Используется при неизвестном объёме совокупности или необходимости обобщения величины, обратной изучаемому признаку.
- 12. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ Используется для расчёта средних темпов и коэффициентов роста в рядах динамики
- 13. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ несгруппированные данные
- 14. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ сгруппированные данные
- 15. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ сгруппированные данные
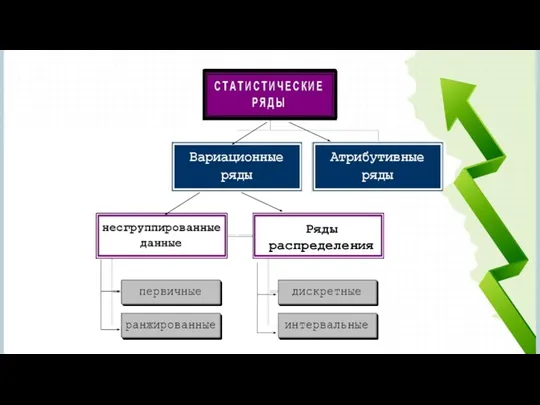
- 16. РЯДЫ РАСПРЕДЕЛЕНИЯ -конкретное значение признака в i- й группе ДИСКРЕТНЫЙ РЯД fi - численность i-ой группы
- 17. СТРУКТУРНЫЕ СРЕДНИЕ ВЕЛИЧИНЫ
- 18. Мо Мода (Мо) - значение признака наиболее часто встречающееся в вариационном ряду.
- 19. Ме Медиана (Ме) - значение варьирующего признака, приходящееся на середину ряда, варианта, делящая ряд на две
- 20. Ряды распределения
- 21. Медиана - центральная варианта при нечетном числе единиц совокупности, при четном числе она равна полусумме серединных
- 22. Моды и медианы первичного ряда не существует! ПЕРВИЧНЫЙ РЯД
- 23. СТРУКТУРНЫЕ СРЕДНИЕ ДЛЯ СГРУППИРОВАННЫХ ДАННЫХ Определение: Кумулятивная частота (Si) результат суммирования предшествующей кумулятивной частоты с частотой
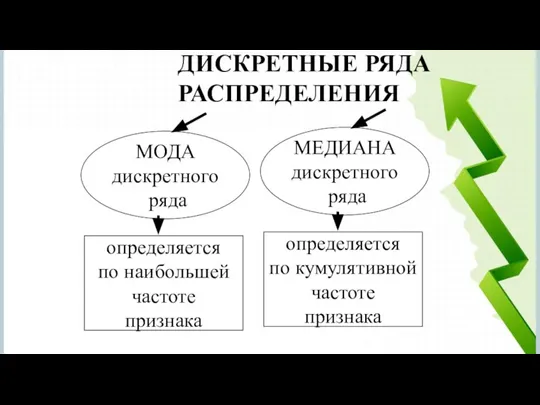
- 24. ДИСКРЕТНЫЕ РЯДА РАСПРЕДЕЛЕНИЯ
- 25. Мода и медиана - конкретные варианты Мода - варианта с максимальной частотой, Медиана - варианта с
- 26. ИНТЕРВАЛЬНЫЙ РЯД РАСПРЕДЕЛЕНИЯ МОДА и МЕДИАНА определяются по специальной методике
- 27. Определение 1 Модальный интервал - интервал с максимальной частотой Определение 2 Медианный интервал - интервал, у
- 28. МОДА
- 29. МЕДДИАНА Астафурова И.С.
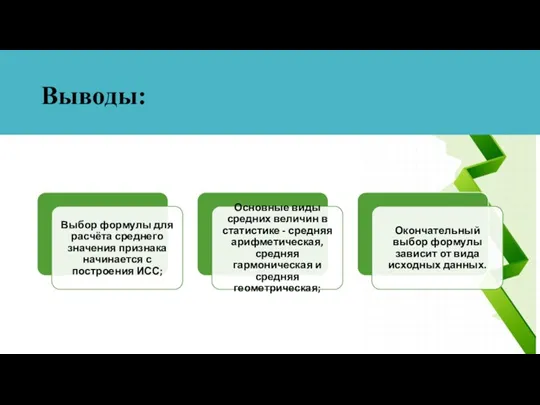
- 30. Выводы:
- 32. Скачать презентацию


























 Математика. 1 класс
Математика. 1 класс Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости Плоская линия в R2
Плоская линия в R2 Виды весов
Виды весов Периметр и площадь прямоугольника. Подготовка к контрольной работе
Периметр и площадь прямоугольника. Подготовка к контрольной работе Тема 1
Тема 1 Приёмы устных вычислений
Приёмы устных вычислений Длина ломанной
Длина ломанной Теорема Пифагора
Теорема Пифагора Множества
Множества Треугольник. Классификация треугольников
Треугольник. Классификация треугольников Параллельность_прямых_в_пространстве_2019
Параллельность_прямых_в_пространстве_2019 Производная функция
Производная функция Различия между разными вариантами технологического процесса. Последовательный анализ
Различия между разными вариантами технологического процесса. Последовательный анализ Геометрия пчелиных сот
Геометрия пчелиных сот Формулы двойного аргумента
Формулы двойного аргумента Сравнение бесконечно малых
Сравнение бесконечно малых Дискретная математика. Повторение арифметических действий
Дискретная математика. Повторение арифметических действий Преобразование графиков функций. Памятка для учащихся
Преобразование графиков функций. Памятка для учащихся Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Функции, их свойства и графики
Функции, их свойства и графики Окружность
Окружность Тригонометрия. Сумма и разность синуса, косинуса
Тригонометрия. Сумма и разность синуса, косинуса Сериал Законы сложения
Сериал Законы сложения Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Свойства параллелограмма
Свойства параллелограмма Решение задач
Решение задач Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда