Основные элементы комбинаторики и бином Ньютона. Тема 11.1

Цель
изучить основные элементы комбинаторики- размещения, перестановки,.

План
Основные задачи комбинаторики
Перестановки
Размещения

Самый простой метод решения комбинаторных задач – перебор всех возможных вариантов
Подсчитать число однобуквенных слов русского языка.
Ответ:10 (а, б, в, ж, и, к, о, с, у, я)
Перечислить виды: 1)треугольников, 2)четырехугольников.
Ответ:1)равносторонний, равнобедренный, разносторонний; остроугольный, прямоугольный, тупоугольный.
2) параллелограмм, прямоугольник, ромб, квадрат, трапеция.
В магазине продают бейсболки трех цветов: синие, красные и черные. Ваня и Андрей покупают себе по одной. Сколько существует различных вариантов покупки?
Ответ:9 вариантов.

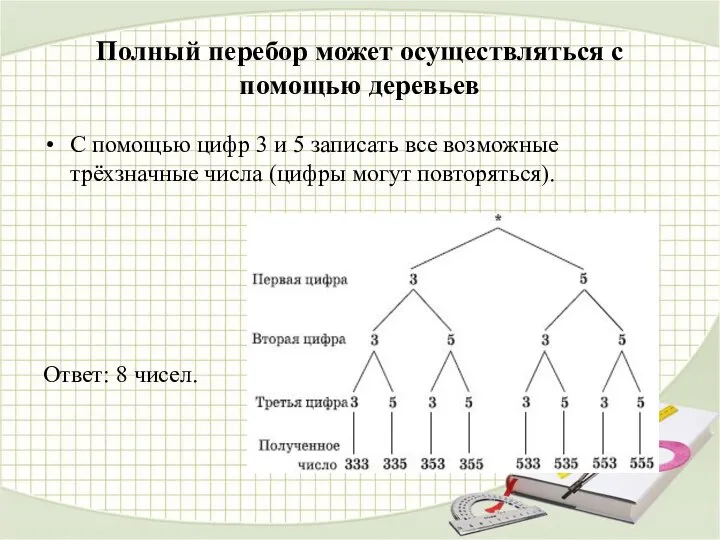
Полный перебор может осуществляться с помощью деревьев
С помощью цифр 3 и 5 записать все возможные трёхзначные числа (цифры могут повторяться).
Ответ: 8 чисел.

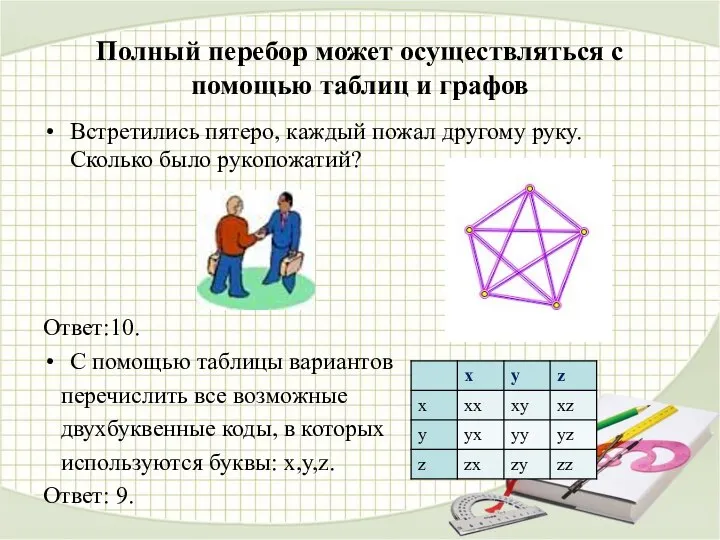
Полный перебор может осуществляться с помощью таблиц и графов
Встретились пятеро, каждый пожал другому руку. Сколько было рукопожатий?
Ответ:10.
С помощью таблицы вариантов
перечислить все возможные
двухбуквенные коды, в которых
используются буквы: x,y,z.
Ответ: 9.

Задача.
В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или жёлтый цвет, причем были использованы все возможные варианты. Сколько команд участвовали в турнире?

При большом количестве имеющихся элементов полный перебор затруднителен. Правило произведения позволяет упростить подсчет числа определенных соединений.
Сформулируем это правило.
Правило произведения
Если существует n вариантов выбора
первого элемента и для каждого из них имеется
m вариантов выбора второго элемента, то существует
n⋅m различных пар с выбранными первым и
вторым элементами.

Задача 1. Сколько различных двузначных чисел можно записать с помощью цифр 0,2,4,6,8 (цифры могут повторятся)?
Ответ: 4∙5 = 20.
Задача 2. В кафе имеются 3 первых блюда, 5 вторых и 2 третьих. Сколькими способами посетитель кафе может выбрать обед, состоящий из первого, второго и третьего блюд?
Ответ: 3∙5∙2 = 30.
Задача 3. Пётр решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор различные по цвету и фасону предметы: 5 пар брюк, 6 камзолов, 3 шляпы, 2 пары сапог. Сколько различных карнавальных костюмов он может составить из этих предметов?
Ответ: 5∙6∙3∙2 = 180.

Основные задачи комбинаторики
Основными задачами комбинаторики считаются следующие:
составление упорядоченных множеств (перестановки);
составление подмножеств данного множества (сочетания)
составление упорядоченных подмножеств данного множества (размещения).
Чтобы отличать задачи на подсчёт числа размещений от задач на подсчёт числа сочетаний, определим, важен или нет порядок в следующих выборках:
а) судья хоккейного матча и его помощник;
б) три ноты в аккорде;
в) «Шесть человек останутся убирать класс!»
г) две серии для просмотра из многосерийного фильма.
Ответ: а)да; б)нет; в)нет; г)да.

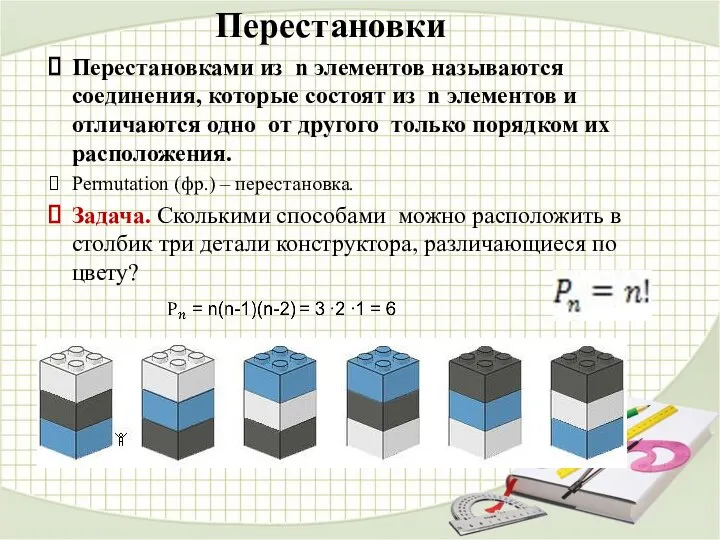
Перестановки
Перестановками из n элементов называются соединения, которые состоят из n элементов и отличаются одно от другого только порядком их расположения.
Permutation (фр.) – перестановка.
Задача. Сколькими способами можно расположить в столбик три детали конструктора, различающиеся по цвету?

Вычислить:
7! 2) 8! 3) 6!-5! 4)
Определение: Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал». Принято считать, что 0! = 1
Задача.
В семье – 6 человек, и за столом в кухне стоят 6 стульев. Семья решила каждый вечер, ужиная рассаживаться на эти стулья по – новому. Сколько дней члены семьи смогут осуществлять задуманное?

Задача.
Сколькими способами можно расставить на полке семь различных книг?
Решение:
Число таких способов равно числу перестановок из семи элементов,
т.е. P7 = 7! = 1 · 2 · 3 · … · 7 =
Ответ: 5040.

Задача.
Имеются 10 различных книг, три из которых – справочники. Сколькими способами можно расставить эти книги на полке так, чтобы все справочники стояли рядом?
Решение:
Т.к. в справочники должны стоять рядом, то будем рассматривать их как одну книгу. Тогда на полке надо расставить 10 – 3+1=8 книг. Это можно сделать P8 способами. Для каждой из полученных комбинаций можно сделать P3 перестановок справочников. Поэтому число способов расположения книг на полке равно произведению:
P8 · P3 = 8! · 3! = 40320 · 6 =
Ответ: 241920.

Размещения
Число всех выборов n элементов из m данных с учётом их порядка называют числом размещений из m элементов по n. (n ≤ m)
Обозначают:

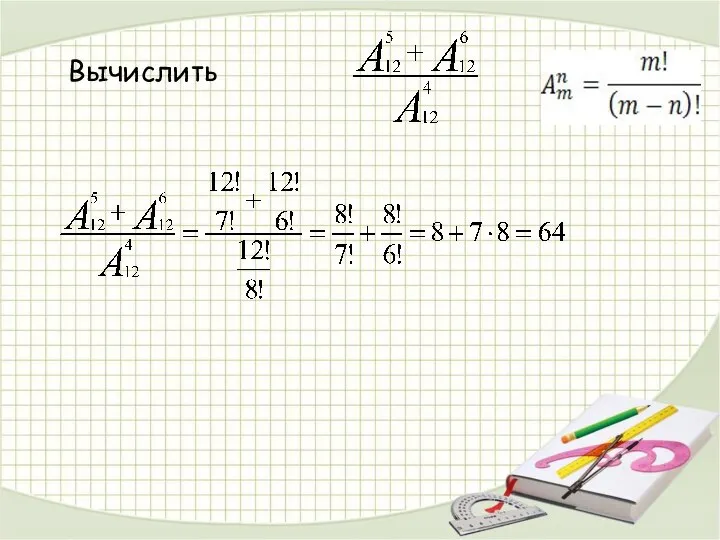
Вычислить

Задача. Решить уравнение:
Решение: n≥ 2 . По формуле
- посторонний корень

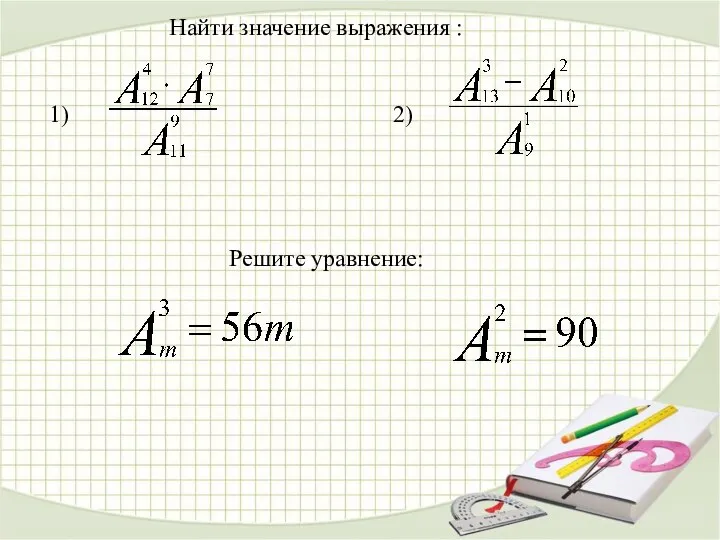
Найти значение выражения :
1) 2)
Решите уравнение:

Размещения
Задача 2. Сколькими
способами могут занять
I, II, III места 8 участниц
финального забега на
дистанции 100 м?
Ответ: 336.
Задача 1. Сколькими способами можно изготовить трёхцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?
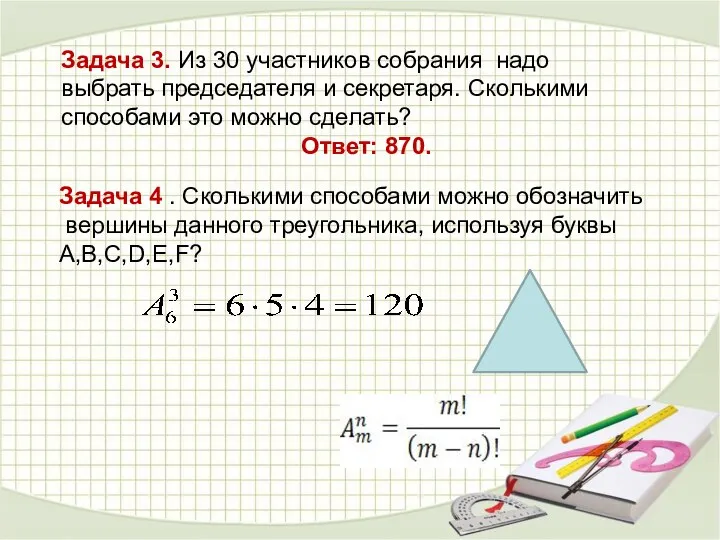
Ответ: 210.

Задача 4 . Сколькими способами можно обозначить
вершины данного треугольника, используя буквы
А,В,С,D,E,F?
Задача 3. Из 30 участников собрания надо
выбрать председателя и секретаря. Сколькими
способами это можно сделать?
Ответ: 870.

Задача.
Сколько существует трехзначных чисел, в которых цифры различные и нечетные.
Решение:
Нечётных цифр пять: 1,3,5,7,9. Их надо разместить на три позиции. Поэтому количество искомых чисел равно числу размещения.
Ответ: 60.