Основные понятия теории множеств, комбинаторики, теории вероятности

Множества
и операции над ними
Множество – это любая совокупность, объединение некоторых объектов произвольной природы.
Объекты, входящие в множество, называются элементами множества
Объекты объединяются в множество по некоторому правилу, следуя которому любой объект, который может быть рассмотрен, однозначно относится к данному множеству или не относится

Множества бывают конечными и бесконечными
Множества обозначаются прописными буквами – A, B, C, …
Элементы множеств – строчными: a, z, x
Принадлежность элемента множеству обозначается символом: z ∈A, x ∉C

Если каждый элемент множества A является одновременно элементом множества B, то множество A является подмножеством множества B, A ⊆ B
Если в множестве B есть элементы не принадлежащие множеству A (т.е. A и B не совпадают), то A ⊂ B
Для любого множества можно рассмотреть множество всех его подмножеств ρ(A) – одноэлементные подмножества, пары элементов, тройки и т.д. и всё множество в целом
Существует множество, в котором нет ни одного элемента – пустое множество ∅.
Пустое множество является подмножеством любого множества

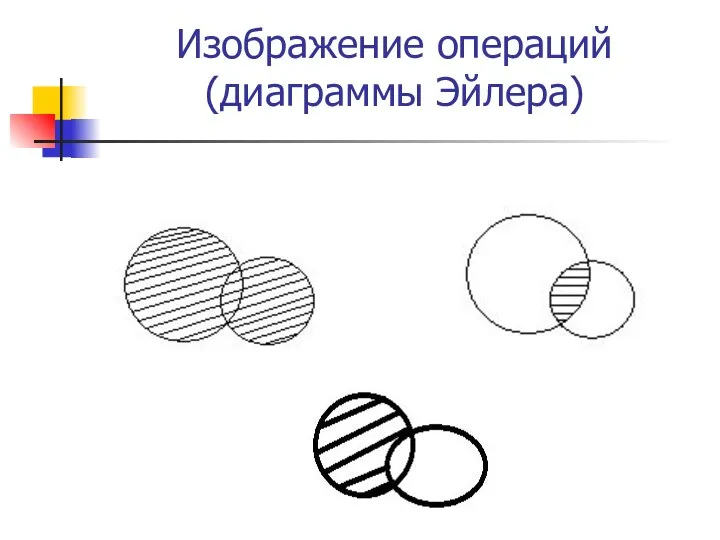
Операции над множествами
1. Сумма или объединение двух множеств ∪
Суммой двух множеств A ∪ B является множество, каждый элемент которого принадлежит либо множеству A, либо множеству B
2. Произведение двух множеств ∩
Произведением двух множеств A ∩ B является множество, каждый элемент которого принадлежит как множеству A, так и множеству B
Пересечение двух множеств может являться пустым множеством ∅

3. Разность множеств \
Разностью двух множеств A\B называется множество состоящее из элементов множества A, не принадлежащих множеству B.
Если B⊂A, то разность A\B называют дополнением множества B в множестве A и обозначают B’A.

Изображение операций
(диаграммы Эйлера)

Основные понятия
теории графов
Граф – это совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа.
Другая формулировка: графом называется непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек

Вершины графа мы будем обозначать латинскими буквами A, B, C, D.
Иногда граф в целом будем обозначать одной заглавной буквой.
Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.
Граф, состоящий только из изолированных вершин, называется нуль-графом.

Если две вершины соединены направленным отрезком, то пара называется упорядоченной, а отрезок называется ребром графа. Если вершины соединены ненаправленным отрезком, то вершины называются неупорядоченными, отрезок, их соединяющий, называется дугой.
Граф, содержащий только ребра, называется ориентированным.
Граф, содержащий только дуги, называется неориентированным.
Пара вершин может соединяться двумя или более ребрами одного направления, такие ребра называются кратными.

Дуга или ребро может начинаться или заканчиваться в одной вершине, такие дуги называются петлями. Считается, что длина петли равна 1.
Вершины, соединенные ребром или дугой называются смежными.
Дуги, имеющие общие вершины называются смежными.
Ребро и любая из двух ее вершин называется инцидентными.
Подграфом GA графа G=(Х,Г) называется граф, в который входит лишь часть вершин графа G, образующих множество А вместе с дугами, соединяющими эти вершины.
Частичным графом GA графа G=(Х,Г) называется граф, содержащий все вершины графа и только часть дуг графа.

Граф, в котором каждая пара вершин соединена ребром, называется полным.
Такой граф можно представить как n–угольник, в котором проведены все диагонали.
Степенью вершины называется число ребер, которым принадлежит вершина.
Обозначение: p (A) – степень вершины A.
Граф, степени всех k вершин которого одинаковы, называется однородным графом степени k.

Дополнением данного графа называется граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф.
Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским.
Путем от A до X называется последовательность ребер, ведущая от A к X, такая, что каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.

Циклом называется путь, в котором совпадают начальная и конечная точка.
Простым циклом называется цикл, не проходящий ни через одну из вершин графа более одного раза.
Длиной пути, проложенного на цикле, называется число ребер этого пути.
Две вершины A и B в графе называются связными (несвязными), если в нем существует (не существует) путь, ведущий из A в B.
Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным.

Деревом называется связный граф, не содержащий циклов.
1. имеется в точности один узел, называемый корнем, в который не входит ни одно ребро,
2. В каждый узел, кроме корня, входит ровно одно ребро,
3. Из корня к каждому узлу идет путь - единственный.
Деревья являются простейшим видом связных графов. Любое дерево с n вершинами содержит n-1 ребер. Число различных деревьев, которые можно построить на n вершинах равно.
Дерево с одной выделенной вершиной называется корневым деревом.
Ориентированный граф, состоящий из нескольких деревьев, называется лесом.

Основные теоремы теории графов
Теорема 1. Удвоенная сумма степеней вершин любого графа равна числу его ребер.
Теорема 2. Число нечетных вершин любого графа четно.
Следствие 1. Нечетное число знакомых в любой компании всегда четно.
Следствие 2. Число вершин многогранника, в которых сходится нечетное число ребер, четно.
Следствие 3. Число всех людей, когда-либо пожавших руку другим людям, нечетное число раз, является четным.

Теорема 3. Во всяком графе с n вершинами, где n больше или равно 2, всегда найдутся две или более вершины с одинаковыми степенями.
Теорема 4. Если в графе с n вершинами (n больше или равно 2) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими.
Теорема 5. Если у графа все простые циклы четной длины, то он не содержит ни одного цикла четной длины.

Теорема 6. Для того, чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень.
Теорема 7. Для того чтобы на связном графе можно было бы проложить цепь АВ, содержащую все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами этого графа.
Теорема 8. Полный граф с пятью вершинами не является плоским.

Элементы комбинаторики
Комбинаторика – раздел математики, в котором изучаются способы пересчета комбинаций элементов, удовлетворяющих тем или иным условиям.
комбинации
Без повторений
Каждый элемент входит в комбинацию не более, чем один раз
С повторениями
Есть элемент, который встречается более одного раза

Характеристики состав и порядок
1 тип. Важен и состав, и порядок (выбрать, разместить) – Размещения
2 тип. Важен только порядок (все элементы участвуют в комбинации) – Перестановки
3 тип. Важен только состав (нет первого элемента, последовательность не важна) – Сочетания
1 и 2 тип – упорядоченные комбинации
Типы комбинаций

Факториал – это произведение всех натуральных чисел до указанного числа n.
Пример.
Понятие факториала

Размещения.
Формулы комбинаций без повторений
Перестановки.
Сочетания.

Пример.

Формулы комбинаций с повторениями
Размещения.
Перестановки.
Сочетания.

Комплекс условий, который может повторяться мысленно бесконечно много раз (опыт, эксперимент) – S
Случайное событие, происходящее или не происходящее в данном опыте – A
Пример.
S – бросаем монетку
A – выпала «решка»
B – выпал «орел»
Элементы теории вероятности

Событие называется достоверным, если оно происходит при каждом испытании в данном эксперименте
Событие называется невозможным, если оно не происходит ни при одном испытании в данном опыте
Пример.
A – наступление дня после ночи, B – выпадение цифры 5 при подбрасывании 10 копеечной монеты
Виды случайных событий

События A и B называются несовместными, если появление одного из них в результате опыта исключает появление другого события
События A и B называются совместными, если появления одного из них не исключает появление другого события
Пример.
A – выпала «решка», B – выпал «орел»
A – досталась конфетка с полки, B – досталась ириска

События называются противоположными (взаимно – дополнительными), если не появление одного из них в результате опыта влечет появление другого
События называются благоприятствующими, если появление одного из них в результате эксперимента влечет появление другого события
Пример.
A – поставлена удовлетворительная оценка, B – поставлена неудовлетворительная оценка
A – все сессионные оценки удовлетворительные, B – начисление стипендии
События называются равновозможными, если по условию данного опыта нет оснований считать одно из них более возможным, чем второе
Пример.
A – выпала «решка», B – выпал «орел»

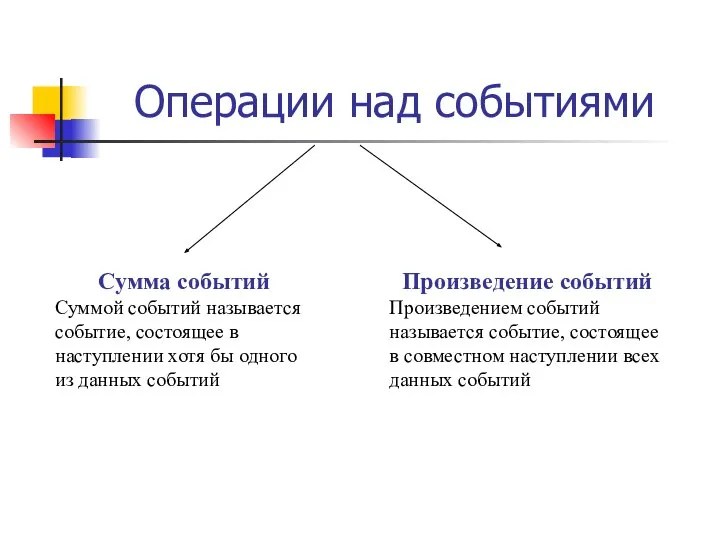
Операции над событиями
Сумма событий
Суммой событий называется событие, состоящее в наступлении хотя бы одного из данных событий
Произведение событий
Произведением событий называется событие, состоящее в совместном наступлении всех данных событий

Пример.
1) A – досталась ириска, B – досталась шоколадная, C – досталась карамелька
Находим сумму двух событий:
A+B – досталась не карамелька
A+C – досталась не шоколадная
B+C – досталась не ириска
2) A – вынули карту пиковой масти, B – вынули даму
Находим произведение событий:
AB – вынули даму пик

Вероятность события
Рассмотрим эксперимент S, с равновозможными исходами. Случайному событию A благоприятствует k исходов (исходы, когда A наступает) и не благоприятствует n-k исходов
Вероятностью события A называется отношение числа благоприятствующих исходов к числу всех исходов данного эксперимента
n – число всех исходов, k – число благоприятствующих исходов

Вероятность события
P (невозможное) = 0
P (достоверное) = 1
Пример
S – бросание игральной кости, A – число выпавших очков кратно 3, B – выпало простое число
,

Теоремы и формулы теории вероятности
Теорема 1: Вероятность суммы двух несовместных событий равно сумме вероятностей этих событий
Следствие: сумма вероятностей противоположных событий равна 1

Теорема 2: Вероятность суммы двух произвольных событий равна сумме вероятностей этих событий без вероятности их произведения

Условная вероятность события A при условии B
Рассмотрим опыт и связанные с ним события A и B
Событию B благоприятствует l исходов, Произведению событий AB благоприятствует q исходов
Отношение называется условной вероятностью события A при условии B

Пример.
S – бросание игральной кости
B – выпадает четное число очков
A – выпадает шестерка
B благоприятствует три исхода l = 3
AB благоприятствует один исход q = 1
Вероятность события A при условии B

Теорема 3: Для условной вероятности P(A/B) справедливы формулы
Теорема 4: Вероятность произведения двух произвольных событий равна вероятности одного из этих событий, умноженное на условную вероятность другого при условии, что первое произошло

Независимые события
Событие A называется независимым от события B, если условная вероятность события A при условии B равна вероятности события A
В противном случае события называются зависимыми

Пример.
S – из колоды в 36 карт вытаскивают одну наугад
A – вытаскивают туз, B – вытаскивают карту красной масти
Выяснить, независимы ли события A и B
Всего 36 исходов, событию A благоприятствует 4 исхода
Событию B благоприятствует 18 исходов, событию AB благоприятствует 2 исхода
события независимы

Теорема 5: Вероятность произведения двух независимых событий равна произведению вероятностей этих событий

Случайные величины
Случайная величина, связанная с некоторым опытом – это величина, которая при осуществлении этого опыта принимает то или иное числовое значение
Пример.
Наружный диаметр трубы, число родившихся в течении суток в разных странах
X – случайная величина
x1, x2, x3, …, xn – её значения
p1, p2, p3, …, pn – вероятности значений

Закон распределения случайной величины (если известны все значения и все вероятности)
p1+ p2+ p3+ …+ pn = 1
Пример.
X – число очков выпавших при подбрасывании игральной кости
Закон распределения

Числовые характеристики случайной величины
1. Математическое ожидание
Это число, равное сумме произведений всех значений величины на вероятности этих значений, MX
Математическое ожидание указывает некоторое среднее число, около которого группируются все значения случайной величины
Пример.

2. Дисперсия
Это математическое ожидание квадрата отклонения случайной величины от её математического ожидания, DX

Дисперсия случайной величины характеризует степень разброса, рассеивания случайной величины относительно её математического ожидания
Пример.
Закон распределения случайной величины:
Найдем математическое ожидание и дисперсию