Основные принципы комбинаторики

Комбинаторика
Комбинаторика – раздел математики, посвященный подсчету количеств разных комбинаций элементов некоторого, обычно конечного, множества
Комбинаторика возникла в XVI веке. Первоначально комбинаторные задачи касались в основном азартных игр. Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Паскаль и Ферма. Дальнейшие развитие комбинаторики связано с именами Якова Бернулли, Лейбница и Эйлера.

Принципы комбинаторики
Принцип сложения
Основные принципы комбинаторики:
Принцип сложения.
Принцип умножения.
Принцип сложения
Задача 1: В классе 7 девочек и 8 мальчиков. Сколькими способами можно выбрать 1 человека для работы у доски?
Решение: Для работы у доски мы можем выбрать девочку 7 способами или мальчика 8 способами.
Общее число способов равно 7+8=15.
Задача 2: В классе 7 человек имеют «5» по математике, 9 человек – «5» по истории, 4 человека имеют «5» и по математике и по истории. Сколько человек имеют пятерку по математике или по истории?
Решение: Так как 4 человека входят и в семерку отличников по математике и в девятку отличников по истории, то сложив «математиков» и «историков», мы дважды учтем этих четверых, поэтому вычтя их один раз из суммы, получим результат 7+9-4=12.
Итак, 12 человек имеют пятерку по математике или по истории.

Принцип сложения
Принцип сложения 1: Если объект a можно получить n способами, объект b можно получить m способами и эти способы различны, то объект «a или b» можно получить n+m.
Принцип сложения 2: Если объект a можно получить n способами, объект b можно получить m способами, то объект «a или b» можно получить n+m-k способами, где k – это количество повторяющихся способов.

Принцип умножения
Задача: На вершину горы ведут 5 дорог. Сколькими способами можно подняться на гору и спуститься с нее?
Решение: Для каждого варианта подъема на гору существует 5 вариантов спуска с горы. Значит всего способов подняться на гору и спуститься с нее 5∙5=25.
Принцип умножения: если объект a можно получить n способами, объект b можно получить m способами, то объект «a и b» можно получить m∙n способами.

Задачи
1) Из 10 коробок конфет, 8 плиток шоколада и 12 пачек печенья выбирают по одному предмету для новогоднего подарка. Сколькими способами это можно сделать?
Решение. Коробку конфет можно выбрать 10 способами, шоколад – 8, печенье – 12 способами.
Всего по принципу умножения получаем способов.

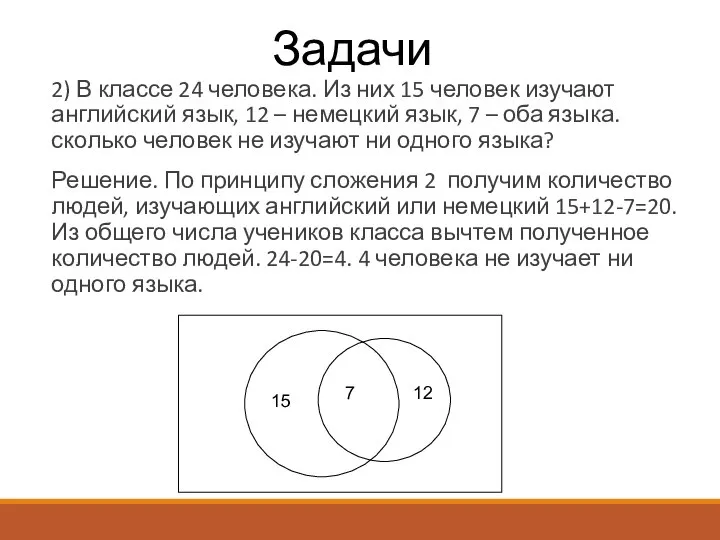
Задачи
2) В классе 24 человека. Из них 15 человек изучают английский язык, 12 – немецкий язык, 7 – оба языка. сколько человек не изучают ни одного языка?
Решение. По принципу сложения 2 получим количество людей, изучающих английский или немецкий 15+12-7=20. Из общего числа учеников класса вычтем полученное количество людей. 24-20=4. 4 человека не изучает ни одного языка.

Задачи
1) Из двух спортивных обществ, насчитывающих по 20 боксеров каждое,
надо выделить по одному боксеру для участия в состязаниях. Сколькими способами это можно сделать?
Решение. По принципу умножения
2) Сколькими способами можно выбрать гласную и согласную букву в слове «экзамен»?
Решение. В слове «экзамен» 3 гласные буквы и 4 согласные.
По принципу умножения

Задачи
3) В классе 20 человек, из них 9 человек изучают язык программирования Бейсик, и 8 человек изучают Паскаль. Сколько человек не изучают языки программирования, если известно, что других языков в этом классе не изучают и каждый человек знает не более одного языка программирования?
Решение. По принципу сложения получим, что 9+8=17
человек изучают языки программирования.
20-17=3 человека не изучают языки программирования.

Задачи
4) От дома до школы существует 6 маршрутов. Сколькими способами можно дойти до школы и вернуться, если дорога «туда» и «обратно» идет по разных маршрутам?
Решение. По принципу умножения
5) Из 3 экземпляров учебника алгебры, 5 экземпляров учебника геометрии и 7 экземпляров учебника истории нужно выбрать по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
Решение. По принципу умножения

Задачи
6) В корзине лежат 15 яблок и 10 апельсинов. Яша выбирает из нее яблоко или апельсин, после чего Полина берет яблоко и апельсин. В каком случае Полина имеет большую свободу выбора: если Яша взял яблоко или если он взял апельсин?
Решение. Если Яша взял яблоко, то по принципу умножения Полина может осуществить свой выбор
способами. Если Яша взял апельсин,
то - способами.
В первом случае у Полины свобода выбора большая.

Размещения
Определение 1
Размещением из n элементов по k называется всякая перестановка из k элементов, выбранных каким-либо способом из данных n.
Пример
Дано множество .
Составим все 2-размещения этого множества.

Число размещений
Теорема 1 Число всех размещений из n элементов по k вычисляется по формуле
Доказательство. Каждое размещение можно получить с помощью k действий:
1) выбор первого элемента n способами;
2) выбор второго элемента (n-1) способами;
и т. д.
k) выбор k –го элемента (n-(k-1))=(n-k+1) способами.
По правилу умножения число всех размещений будет
n(n-1)(n-2)…(n-k+1). Теорема доказана.

Число размещений
Замечание. Формулу для числа размещений можно записать в виде
Действительно

Пример
Абонент забыл последние 3 цифры номера телефона. Какое максимальное число номеров ему нужно перебрать, если он вспомнил, что эти последние цифры разные?
Решение.
Задача сводится к поиску различных перестановок 3 элементов из 10 ( так как всего цифр 10). Применим формулу для числа перестановок.

Размещения с повторениями
Определение 2
Размещением с повторением из n элементов по k называется всякая перестановка из k элементов, выбранных каким-либо способом из данных n элементов возможно с повторениями.
Пример
Дано множество
Составим 2- размещения с повторениями:

Число размещений с повторениями
Теорема 2. Число k- размещений с повторениями из
n элементов вычисляется по формуле
Доказательство. Каждый элемент размещения
можно выбрать n способами. По правилу
умножения число всех размещений с повторениями
равно

Пример
Сколько существует номеров машин?
Решение. Считаем, что в трех буквах номера машины не используются буквы «й», «ы», «ь», «ъ», тогда число перестановок букв равно .
Число перестановок цифр равно .
По правилу умножения получим число номеров машин

Перестановки
Определение 1
Перестановкой из n элементов называется всякий способ нумерации этих элементов
Пример 1 Дано множество . Составить все перестановки этого множества.
Решение.

Число перестановок
Теорема 1. Число всех различных перестановок из n элементов равно n!
Замечание.
Например,
Считают, что 0!=1
читается «n факториал» и вычисляется по формуле

Число перестановок
Доказательство теоремы 1.
Любую перестановку из n элементов можно получить с помощью n действий:
выбор первого элемента n различными способами,
выбор второго элемента из оставшихся (n-1) элементов, т.е. (n-1) способом,
выбор третьего элемента (n-2) способами,
……
n) выбор n-го элемента 1 способом.
По правилу умножения число всех способов выполнения действий, т.е. число перестановок, равно
Теорема доказана.

Перестановки
Число всех перестановок обозначается
Итак,
Пример
В команде 6 человек. Сколькими способами они могут построиться для приветствия?
Решение
Число способов построения равно числу перестановок 6 элементов, т.е.

Перестановки с повторениями
Теорема 2
Число перестановок n – элементов, в котором есть одинаковые элементы, а именно элементов i –того типа
( ) вычисляется по формуле
где
Доказательство. Так как перестановки между одинаковыми элементами не изменяют вид перестановки в целом, количество перестановок всех элементов множества нужно разделить на число перестановок одинаковых элементов.

Пример
Задача: Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»?
Решение: В слове «экзамен» все буквы различны, поэтому используем формулу для числа перестановок без повторений
В слове «математика» 3 буквы «а», 2 буквы «м», 2 буквы «т», поэтому число перестановок всех букв разделим на число перестановок повторяющихся букв:

Задачи
1)Сколькими способами можно составить список из 8 учеников, если у них различные инициалы?
Решение
Задача сводится к подсчету числа перестановок ФИО.

Задачи
2)Сколькими способами можно составить список 8 учеников, так, чтобы два указанных ученика располагались рядом?
Решение
Можно считать двоих указанных учеников за один объект и считать число перестановок уже 7 объектов, т.е.
Так как этих двоих можно переставлять местами друг с другом, необходимо умножить результат на 2!

Задачи
3) Сколькими способами можно разделить 11 спортсменов на 3 группы по 4, 5 и 2 человека соответственно?
Решение. Сделаем карточки: четыре карточки с номером 1, пять карточек с номером 2 и две карточки с номером 3. Будем раздавать эти карточки с номерами групп спортсменам, и каждый способ раздачи будет соответствовать разбиению спортсменов на группы. Таким образом нам необходимо посчитать число перестановок 11 карточек, среди которых четыре карточки с одинаковым номером 1, пять карточек с номером 2 и две карточки с номером 3.

Задачи
4) Сколькими способами можно вызвать по очереди к доске 4 учеников из 7?
Решение. Задача сводится к подсчету числа размещений из 7 элементов по 4

Задачи
5)Сколько существует четырехзначных чисел, у которых все цифры различны?
Решение. В разряде единиц тысяч не может быть нуля, т.е возможны 9 вариантов цифры.
В остальных трех разрядах не может быть цифры, стоящей в разряде единиц тысяч (так как все цифры должны быть различны), поэтому число вариантов вычислим по формуле размещений без повторений из 9 по 3
По правилу умножения получим

Задачи
6)Сколько существует двоичных чисел, длина которых не превосходит 10?
Решение. Задача сводится к подсчету числа размещений с повторениями из двух элементов по 10

Задачи
7)В лифт 9 этажного дома зашли 7 человек. Сколькими способами они могут распределиться по этажам дома?
Решение. Очевидно, что на первом этаже никому не надо выходить. Каждый из 7 человек может выбрать любой из 8 этажей, поэтому по правилу умножения получим
Можно так же применить формулу для числа размещений с повторениями из 8 (этажей) по 7(на каждого человека по одному этажу)

Задачи
8)Сколько чисел, меньше 10000 можно написать с помощью цифр 2,7,0?
Решение. Так как среди цифр есть 0, то, например запись 0227 соответствует числу 227, запись 0072 соответствует числу 72, а запись 007 соответствует числу 7. Таким образом, задачу можно решить, используя формулу числа размещений с повторениями