Слайд 2Алгоритм нахождения обратной матрицы
1
Определяем, квадратная ли
матрица. Если нет, то
обратной матрицы для
нее

не существует.
Слайд 32
Находим определитель матрицы.
Если он равен нулю, то обратной
матрицы не существует.

Слайд 43
Заменяем каждый элемент матрицы
его алгебраическим дополнением.

Слайд 54
Полученную матрицу транспонируем.

Слайд 65
Каждый элемент полученной
матрицы делим на определитель
исходной матрицы. Получаем
матрицу, обратную

к данной.
Слайд 76
Делаем проверку. Для этого
перемножаем полученную и исходную
матрицы. Должна получиться
единичная матрица.

Слайд 8Пример 1.
Найти матрицу, обратную к матрице

Слайд 9Применяем алгоритм нахождения обратной матрицы.
Решение:
Находим определитель:
Матрица квадратная, следовательно обратная матрица для

Слайд 10Находим алгебраические дополнения каждого элемента матрицы:
3
Составляем из полученных значений матрицу:

Слайд 11Транспонируем ее:
Каждый элемент матрицы делим на определитель Δ=1 и получаем обратную матрицу:
4
5

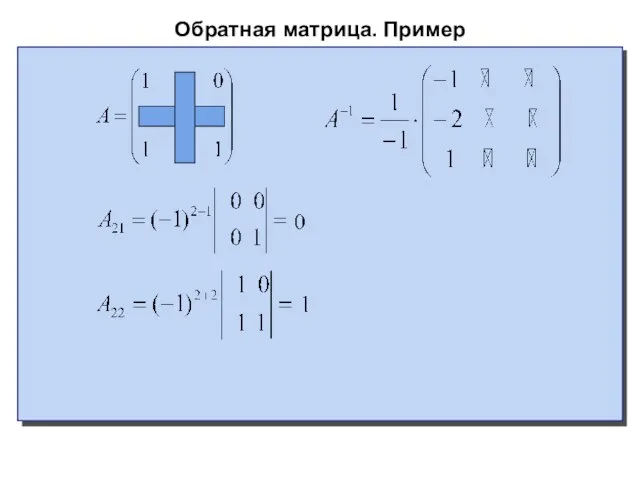
Слайд 13Обратная матрица. Пример
Пример
Найти обратную матрицу к матрице
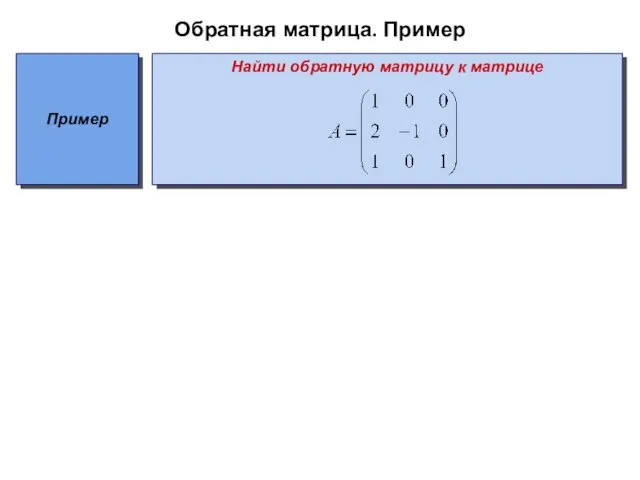
Слайд 14Обратная матрица. Пример
Пример
Найти обратную матрицу к матрице
Решение
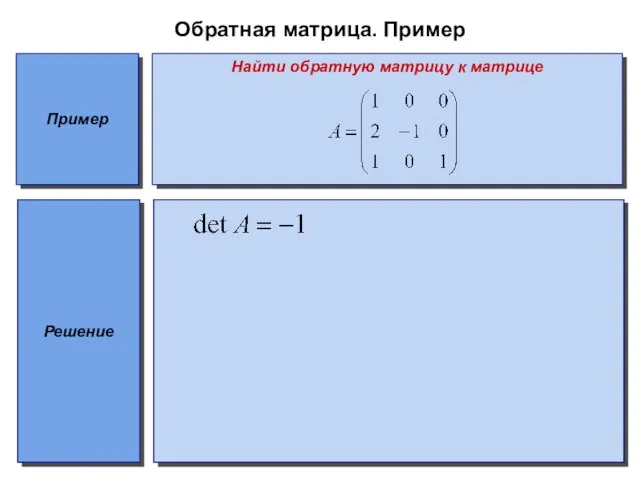
Слайд 15Обратная матрица. Пример
Пример
Найти обратную матрицу к матрице
Решение
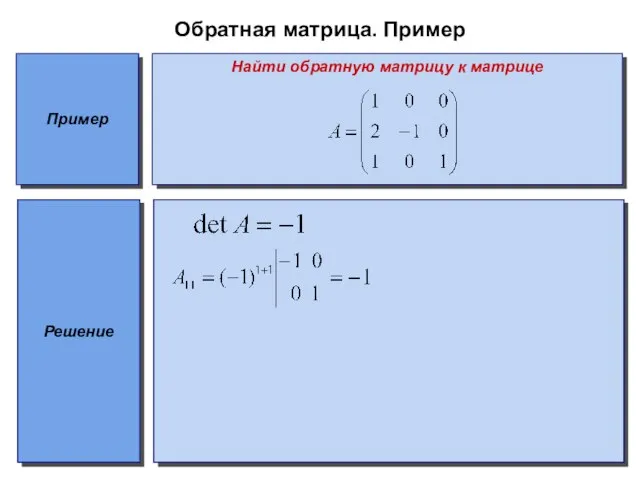
Слайд 16Обратная матрица. Пример
Пример
Найти обратную матрицу к матрице
Решение
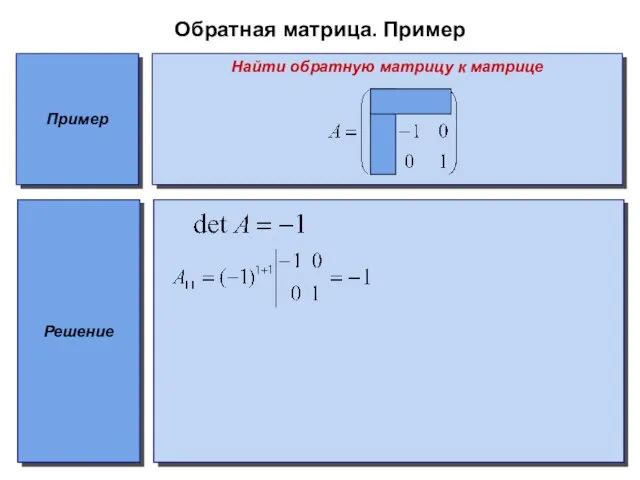
Слайд 17Обратная матрица. Пример
Пример
Найти обратную матрицу к матрице
Решение
Слайд 18Обратная матрица. Пример
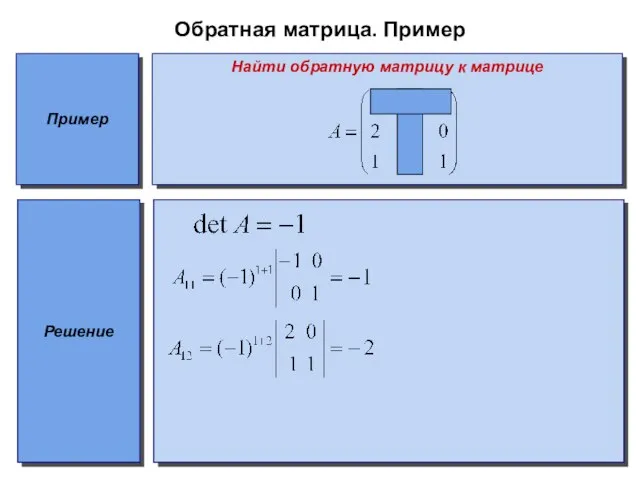
Пример
Найти обратную матрицу к матрице
Решение
Слайд 19Обратная матрица. Пример
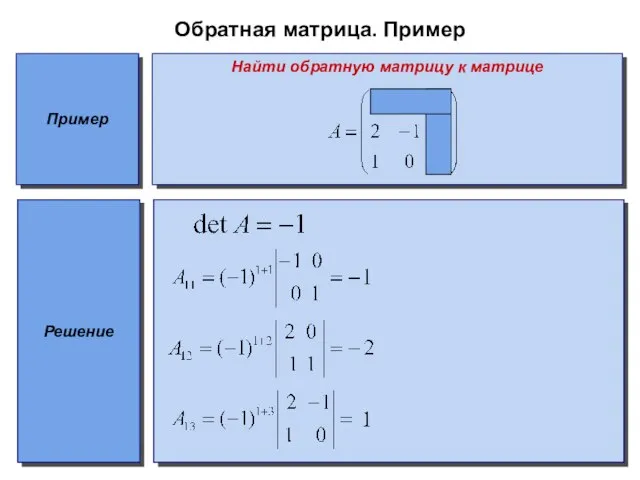
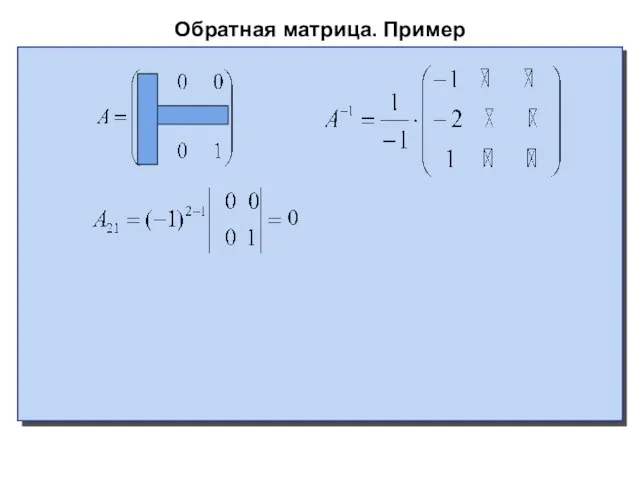
Пример
Найти обратную матрицу к матрице
Решение











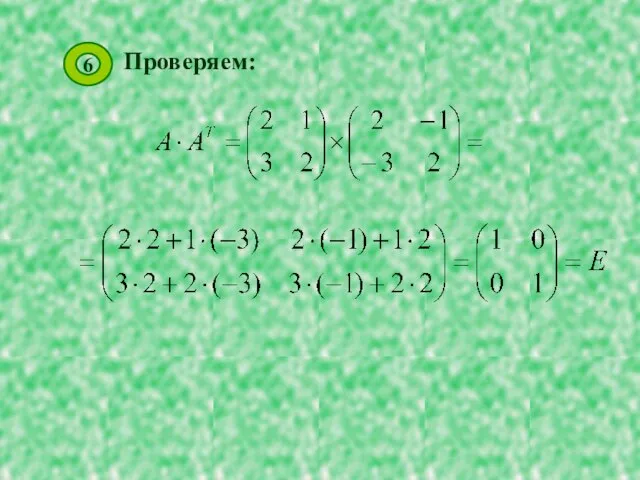








 Презентация на тему ГИА 2013. Модуль Геометрия №10
Презентация на тему ГИА 2013. Модуль Геометрия №10  Шар и многоугольник
Шар и многоугольник Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Степенная функция (занятия 1, 2, 3)
Степенная функция (занятия 1, 2, 3) Решение треугольников
Решение треугольников Сумма
Сумма Решение уравнений
Решение уравнений Точечные и интервальные оценки
Точечные и интервальные оценки 2.7. Теория систем линейных алгебраических уравнений
2.7. Теория систем линейных алгебраических уравнений Сложение и умножение вероятностей
Сложение и умножение вероятностей Как построить график функции y=f(x+l)+m из графика функции y=f(x)
Как построить график функции y=f(x+l)+m из графика функции y=f(x) Углы и многоугольники
Углы и многоугольники Скалярное произведение векторов. (Лекция 5)
Скалярное произведение векторов. (Лекция 5) Кривые второго порядка
Кривые второго порядка Algorytmy i struktury danych
Algorytmy i struktury danych Логические задачи. Мастер-класс
Логические задачи. Мастер-класс Центральные и вписанные углы
Центральные и вписанные углы Тригонометрический круг
Тригонометрический круг Изучение таблицы деления
Изучение таблицы деления Вычислительная геометрия. Стороны треугольника
Вычислительная геометрия. Стороны треугольника Решение задач с помощью систем уравнения
Решение задач с помощью систем уравнения Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математике Функции и последовательности
Функции и последовательности Prezentatsia_k_uroku_matematiki_6_klass
Prezentatsia_k_uroku_matematiki_6_klass Презентация на тему Параллелограмм и трапеция
Презентация на тему Параллелограмм и трапеция  Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса
Конус. Виды конусов. Сечения конуса. Площадь боковой поверхности конуса. Площадь полной поверхности конуса Признак параллельности плоскостей
Признак параллельности плоскостей Несобственные интегралы. Геометрические приложения определенного интеграла
Несобственные интегралы. Геометрические приложения определенного интеграла