Площадь поверхности вращения

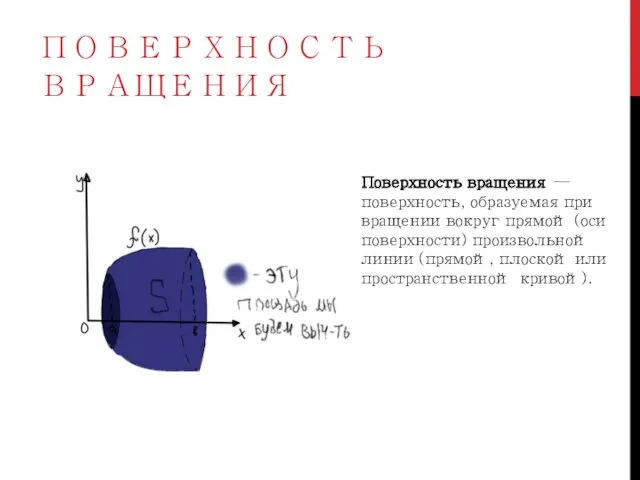
ПОВЕРХНОСТЬ ВРАЩЕНИЯ
Поверхность вращения —поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой).

Для того, чтобы вычислить данную площадь, необходимо воспользоваться формулой:
Как её вывести?
Я рада, что вы спросили. Для начала зададим плоскость вращения:
Плоскость задана.

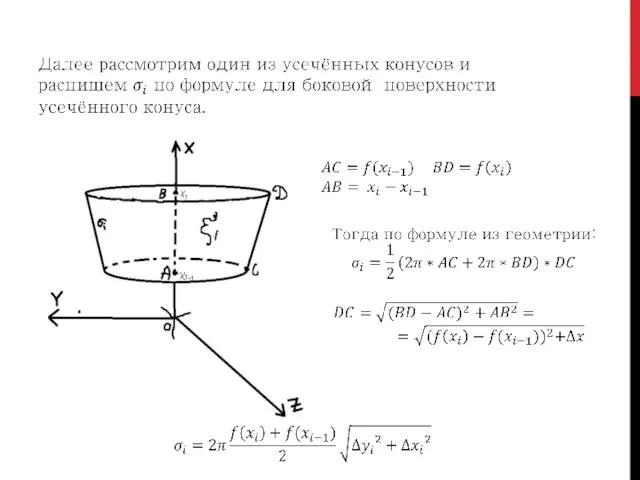
При очень большом приближении (и частом делении), части, на которые мы поделили фигуру становятся усеченными конусами. Из суммы боковых поверхностей эти конусов и складывается площадь поверхности нашей фигуры.

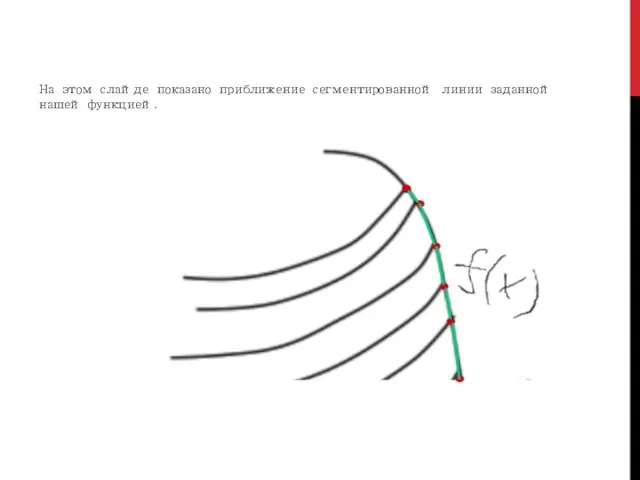
На этом слайде показано приближение сегментированной линии заданной нашей функцией.

Вторая часть этого выражения это определённый интеграл:

А первое слагаемое после использования свойства непрерывной функции приводится к виду:
А вот это сумма всех образующих, т.е. длина линии

А ТЕПЕРЬ ДАВАЙТЕ ДОКАЖЕМ РАЗЛИЧНЫЕ ЧАСТНЫЕ СЛУЧАИ, ЭТО ЖЕ ТАК КРУТО
(Можно ненадо я хочу спать)

ДРУГИЕ СЛУЧАИ