Содержание
- 2. Функция y = f(x, у) называется однородной функцией n – ого порядка, если при умножении каждого
- 3. Однородное дифференциальное уравнение вида (1) приводится к уравнению с разделяющимися переменными при помощи подстановки:
- 4. Однородное уравнение часто задается в дифференциальной форме: Уравнение (2) будет однородным, если P(x; y) и Q(x;
- 5. Пример. Уравнение является однородным, так как функции: - однородные второго порядка Пусть:
- 6. Линейные дифференциальные уравнения ДУ первого порядка называется линейным, если его можно записать в виде: Метод Бернулли.
- 7. Подставим в уравнение (3): Подберем функцию v(x) так, чтобы выражение, стоящее в скобках было равно нулю,
- 8. Пример. Таким образом, общее решение уравнения: При нахождении функции v(x) произвольная постоянная С не прибавляется При
- 10. Скачать презентацию







 Векторы. 9 класс
Векторы. 9 класс Задачи для всех-всех-всех
Задачи для всех-всех-всех Алгебра. Лекция 3
Алгебра. Лекция 3 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Пифагор и его школа
Пифагор и его школа Логарифмические уравнения с параметром
Логарифмические уравнения с параметром Практика. Дискретная математика
Практика. Дискретная математика Признаки делимости чисел
Признаки делимости чисел Задачи по стереометрии. Подготовка к ЕГЭ
Задачи по стереометрии. Подготовка к ЕГЭ Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Приемы решения экономических задач в ЕГЭ
Приемы решения экономических задач в ЕГЭ Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Теорема, обратная теореме Пифагора
Теорема, обратная теореме Пифагора Графическое представление газовых законов
Графическое представление газовых законов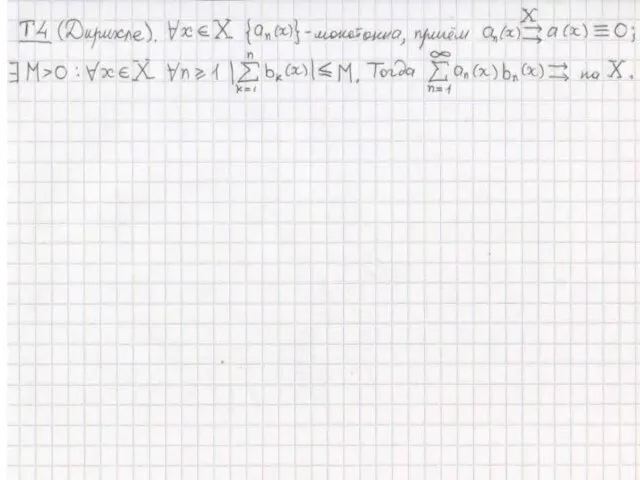 Свойства равномерно-сходящихся плоскостей и рядов
Свойства равномерно-сходящихся плоскостей и рядов Презентация на тему Скалярное произведение векторов (9 класс)
Презентация на тему Скалярное произведение векторов (9 класс)  Множества и его элементы
Множества и его элементы Правильные многоугольники. Геометрия
Правильные многоугольники. Геометрия Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом.
Вектор Вектор – отрезок, для которого указано, какой из его концов считается началом, а какой – концом. Математический анализ. Неопределенный интеграл
Математический анализ. Неопределенный интеграл Юбилейный ЕГЭ по математике Вперед! Только вперед!
Юбилейный ЕГЭ по математике Вперед! Только вперед! d694e47421834013895052f206be4c31
d694e47421834013895052f206be4c31 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Решение неравенств с одной переменной
Решение неравенств с одной переменной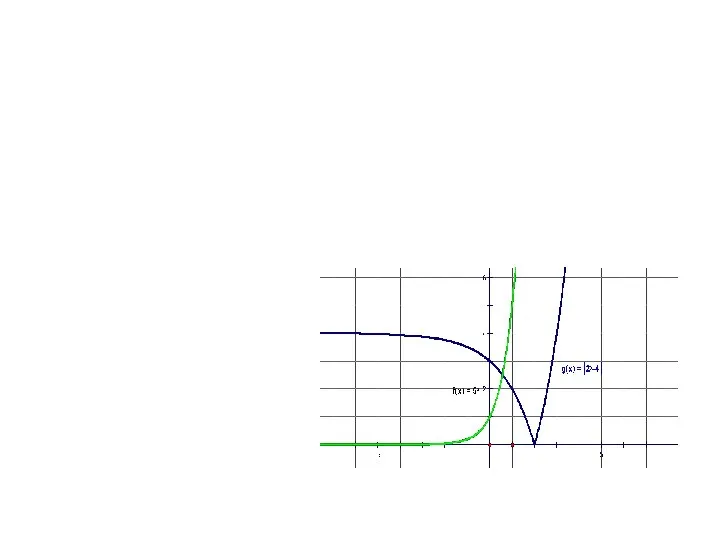 Показательные уравнения
Показательные уравнения ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей
ИПАР по математике. Задача на проценты. Тема: математика в профессии моих родителей Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Решение уравнений производная
Решение уравнений производная