РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4)
Содержание
- 2. На практике обычно требуется определить вероятности событий непосредственное экспериментальное воспроизведение которых затруднительно. Например, оценить вероятность исхода
- 3. Применение косвенных методов в той или иной мере всегда сводится к применению основных теорем теории вероятностей:
- 4. §1. Теорема сложения вероятностей Теорема. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. Доказательство.
- 5. §1. Теорема сложения вероятностей Замечание. Теорему можно обобщить на случай любого конечного числа несовместных событий. Вероятность
- 6. Пример 1 Имеется три склада боеприпасов. Эксперимент: наугад сбрасывается одна бомба. Событие Аi : бомба попала
- 7. §1. Теорема сложения вероятностей Следствие 1. Если несовместные события образуют полную группу, то сумма их вероятностей
- 8. §1. Теорема сложения вероятностей Следствие 2. Сумма вероятностей противоположных событий равна единице. Доказательство. 8 Лекция 2.
- 9. §2. Теорема умножения вероятностей Событие А называется независимым от события В, если вероятность события А не
- 10. §2. Теорема умножения вероятностей Вероятность события А, найденная при условии, что событие В произошло, называется условной
- 11. §2. Теорема умножения вероятностей Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на
- 12. §2. Теорема умножения вероятностей Доказательство. 12 Лекция 2. Теоремы о вероятностях сложных событий
- 13. §2. Теорема умножения вероятностей Замечание. Теорему можно обобщить на случай любого конечного числа событий. Вероятность произведения
- 14. Пример 2 Всего в урне два белых и три чёрных шара. Эксперимент: наугад последовательно извлекают из
- 15. §2. Теорема умножения вероятностей Следствие 1. Если событие А не зависит от события В, то и
- 16. Пример 3 Эксперимент: монета наугад подбрасывается три раза. Событие Аi : выпал «герб» при i-м броске,
- 17. §2. Теорема умножения вероятностей Теорема. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности
- 18. §2. Теорема умножения вероятностей Доказательство. 18 Лекция 2. Теоремы о вероятностях сложных событий
- 19. §3. Формула полной вероятности Следствием обеих основных теорем – теоремы сложения вероятностей и теоремы умножения вероятностей
- 20. Пример 4 Имеется две винтовки с «оптикой» и три обычных винтовки. Вероятность попадания для винтовки с
- 21. §4. Теорема гипотез (формула Байеса) Следствием теоремы умножения вероятностей и формулы полной вероятности является теорема гипотез
- 22. Пример 4 (продолжение) 22 Лекция 2. Теоремы о вероятностях сложных событий Имеется две винтовки с «оптикой»
- 24. Скачать презентацию





















 Комплексные числа и действия над ними
Комплексные числа и действия над ними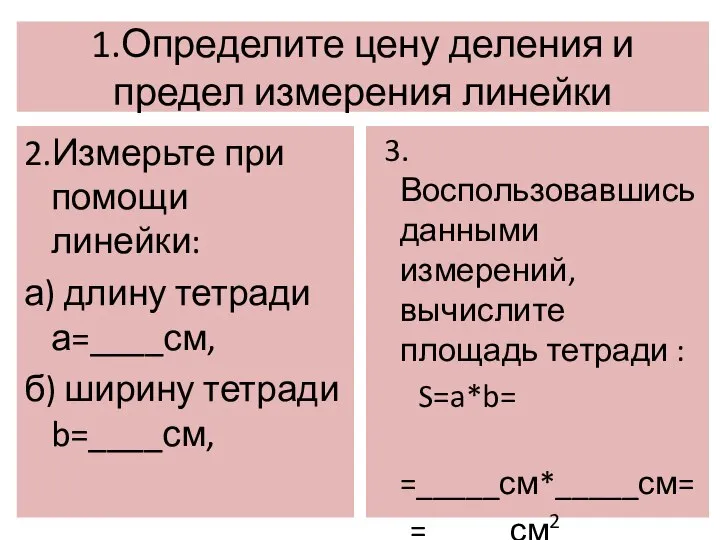 Цена деления и предел измерения линейки
Цена деления и предел измерения линейки Состав чисел
Состав чисел Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу
Властивості і графіки тригонометричних функцій. Графік тангенса та котангенса числового аргументу Реши уравнения
Реши уравнения Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Треугольники
Треугольники Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Решение уравнений с одной переменной
Решение уравнений с одной переменной Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Признаки параллельности прямых
Признаки параллельности прямых Умножение и деление отрицательных чисел. Урок-путешествие
Умножение и деление отрицательных чисел. Урок-путешествие Преобразование графиков вида у=f(х±а)
Преобразование графиков вида у=f(х±а) Математика. Числа до 20
Математика. Числа до 20 Какой функции соответствует график
Какой функции соответствует график Контрольная работа
Контрольная работа Теория антагонистических игр. Задачи для выполнения
Теория антагонистических игр. Задачи для выполнения Интерактивный тренажёр Весёлый счёт. Математика 1 класс
Интерактивный тренажёр Весёлый счёт. Математика 1 класс Задачи на перебор вариантов
Задачи на перебор вариантов Решение тригонометрических уравнений
Решение тригонометрических уравнений Задачи на нахождение неизвестного третьего слагаемого
Задачи на нахождение неизвестного третьего слагаемого Дифференциальные уравнения высшего порядка
Дифференциальные уравнения высшего порядка Итогово-обобщающий урок. Площадь. Теорема Пифагора
Итогово-обобщающий урок. Площадь. Теорема Пифагора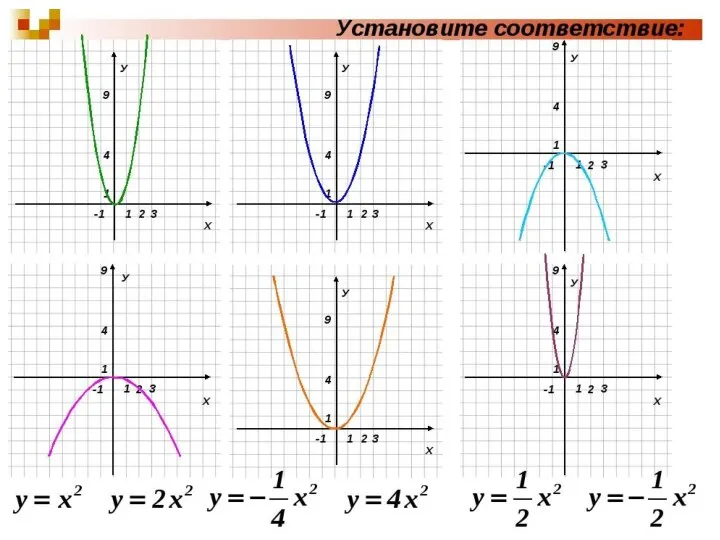 Графики функций
Графики функций Результант. Литература
Результант. Литература Занятие 45. Формулы двойного угла. Формулы половинного угла
Занятие 45. Формулы двойного угла. Формулы половинного угла