Путешествие по стране Дроби. 5 класс

План урока
1. Подготовка к путешествию
2. Путешествие
3. Итог урока
4. Домашнее задание

В путешествие мы отправимся на поезде. Но в железнодорожном депо сообщили, что исправного поезда нет. Есть только паровоз и несколько вагонов, находящихся на разных путях. Некоторые из них неисправны. Нам необходимо найти целые вагоны и прикрепить их к паровозу.
Для этого необходимо выполнить следующее задание:
На следующем слайде записаны примеры. Решите их, найдите ответы на карточках-вагонах, расположенных вокруг. Каждый ответ является первым числом следующего примера. Из правильных ответов мы и составим наш поезд.

Строим поезд!
12,11
13,1
16,2
19,68
6,63
15,12
19,86
5,4
4,55

Счастливого пути !

Карта путешествия
деревня "Историческая"
горы Мозгодром
Крушение
Волшебный лес

С незапамятных времён при дележе добычи охотники имели дело с долями целого. Трудно было обходиться без дробей и при измерении различных величин.
Древние египтяне использовали лишь единичные дроби ½, 1/3, ¼ и т. д., то есть дроби, числители которых равны 1.
Все вычисления с дробными числами производились с помощью этих единичных дробей, что было очень сложно. Поэтому их могли выполнять лишь специально обученные писцы.
Современная форма записи обыкновенных дробей стала применяться лишь в 18 в. Первым дробную черту стал применять арабский учёный ал-Халар. В Европе дробную черту для записи обыкновенных дробей использовал итальянский математик Леонардо Пизанский, названный также Фибоначчи (то есть сын Боначчи).
Долгое время действия с дробными числами считались по праву очень сложными. Недаром у немцев сохранилось выражение «попасть в дробь», что означает «попасть в тупик, в трудное положение». Даже ещё в 18 в. овладение действиями с дробными числами, которые иногда назывались ломаными числами, считалось очень трудным делом. Поэтому математики искали другие формы записи дробных чисел, которые позволяли бы упростить действия с ними. Такой формой оказалась десятичная запись дробных чисел.
Описал правила действий над десятичными дробями среднеазиатский математик и астроном Гиясэддин Ал-Каши в своей книге «Ключ к арифметике» (1427 г.). Только через 150 лет фламандский инженер и математик Симон Стевин открыл заново десятичные дроби и описал правила действий над ними. Запятую после целой части десятичной дроби предложил ставить немецкий математик Иоганн Кеплер (1571 – 1630).

Египетский писец

Леонардо Пизанский (Фибоначчи) (1180-1240гг.) - итальянский математик. Родился в Пизе. Начальное образование получил в Бугие (Алжир), под руководством местного учителя овладел арифметикой и алгеброй арабов. Посетил многие страны Европы и Востока, пополняя свои знания по математике.
Издал 3 книги: "Книгу об абаке" (1202г.), где абак рассматривался не столько как прибор, сколько как исчисление вообще, "Практическую геометрию" (1220г.) и "Книгу квадратов" (1225г.). По первой книге многие поколения европейских математиков изучали "индийскую позиционную систему счисления. В ней Леонардо впервые в Европе привел отрицательные числа, которые рассматривал как долг. Изложение материала было оригинальным и изящным. Леонардо сделал и собственные открытия, в частности положил начало разработке вопросов, связанных с числами Фибоначчи, и предложил оригинальный прием извлечения кубического корня. Труды Леонардо получили распространение только в конце XV в., когда Лука Пачоли переработал их и опубликовал в своей книге "Сумма" (Венеция, 1494г).
Леонардо Пизанский (Фибоначчи)

Стевин (Stevin) Симон (1548, Брюгге, — 1620, Гаага), нидерландский учёный и инженер. С 1583 преподавал в Лейденском университете. В 1600 организовал инженерную школу при Лейденском университете, где читал лекции по математике. Работа С. "Десятина" (De Thiende, 1585) посвящена десятичной системе мер и десятичным дробям, которые С. ввёл в употребление (в Европе).
Трактат Стевина содержал практическое описание арифметики десятичных дробей, а также пылкую и хорошо аргументированную пропаганду полезности их применения, в частности, в системах мер и монетном деле.
Десятичную запятую (в Англии — точку) ещё не придумали, и Стевин для ясности указывал над каждой цифрой (или после неё) заключённый в кружок её номер разряда, положительный для целой части,
Симон Стевин

КЕПЛЕР, ИОГАНН (Kepler, Johann) (1571–1630), немецкий астроном. Родился 27 декабря 1571 в Вейль-дер-Штаде, позднее вошедшем в княжество Вюртемберг. Окончив церковную школу в Альдерберге, в 1586 поступил в высшее духовное училище при Маульборнском монастыре. В 1589 был принят в Тюбингенский университет, где в течение трех лет изучал теологию, математику и философию.
В 1591 Кеплер защитил магистерскую диссертацию, в 1593 окончил университет и был рекомендован на должность профессора математики в гимназии Граца. Главным достижением Кеплера в этот период стало открытие третьего закона движения планет.
Этот закон был сформулирован в сочинении Гармония мира (De Harmonice Mundi, 1619). Следующие 9 лет Кеплер трудился над составлением таблиц положения планет, основанных на новых законах их движения.
Иоганн Кеплер

5,02
-3,89
*3,1
+5,697
*5
+3,74
:0,3
1,13
3,503
9,2
46
49,74
165,8

Решить уравнение: 5x-3,7=22,8
x=5,3

Сформулируйте правило сравнения десятичных дробей

10х + 3,72 = 5,69
Решить уравнение:
x=0,197

Как увеличить десятичную дробь в 10, 100, 1000 и т. д. раз?

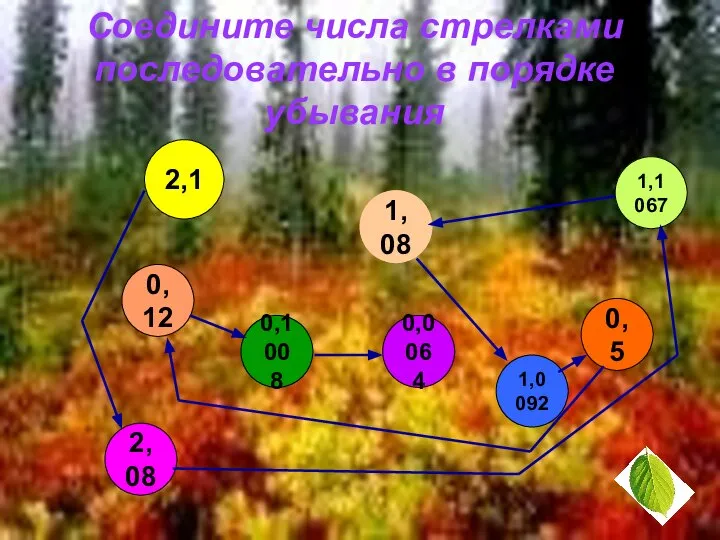
Соедините числа стрелками последовательно в порядке убывания
2,1
0,12
2,08
0,1008
0,0064
1,0092
1,08
0,5
1,1067

Восстановите запятые
в примерах:
а) 3 2 + 1 8 = 5;
б) 3 – 1 0 8 = 2 9 2;
в) 4 2 + 1 7 = 2 1 2;
г) 7 3 6 – 1 2 = 6 1 6;
д) 6 3 – 2 7 = 6 0 3;
е) 5 0 7 – 4 = 4 6 7.
,
,
,
,
,
,
,
,
,
,
,
,
,

С каким настроением я ухожу с урока:

Ты молодец! Ты всё понял! Тебе всё удалось!

Ты еще не всё понял. Тебе надо немного потрудиться!

1. Если в данном числе перенести запятую через одну цифру вправо и сложить с данным числом, то получится 40,92. Найдите данное число.
2. Если в данном числе перенести запятую вправо через одну цифру и из результата вычесть данное число, то получится 31,86. Найдите данное число.