Содержание
- 2. Вечные истины Математику многие любят за ее вечные истины: дважды два всегда четыре, сумма четных чисел
- 3. Реальная жизнь оказывается не такой простой и однозначной. Исходы многих явлений невозможно предсказать заранее, какой бы
- 4. Случай имеет свои законы ! Однако случай тоже имеет свои законы, которые начинают проявляться при многократном
- 5. «Теория вероятностей есть в сущности не что иное, как здравый смысл, сведенной к исчислению» Лаплас Теория
- 6. В настоящее время Теория вероятностей имеет статус точной науки наравне с арифметикой, алгеброй, геометрией, тригонометрией и
- 7. Предыстория теории вероятностей Богатый материал для наблюдения за случайностью на протяжении многих веков давали азартные игры.
- 8. У истоков науки В археологических раскопках специально обработанные для игры кости животных встречаются, начиная с V
- 9. Теория вероятностей — раздел математики, изучающий вероятности событий. Теория вероятностей разрабатывает методы, с помощью которых можно
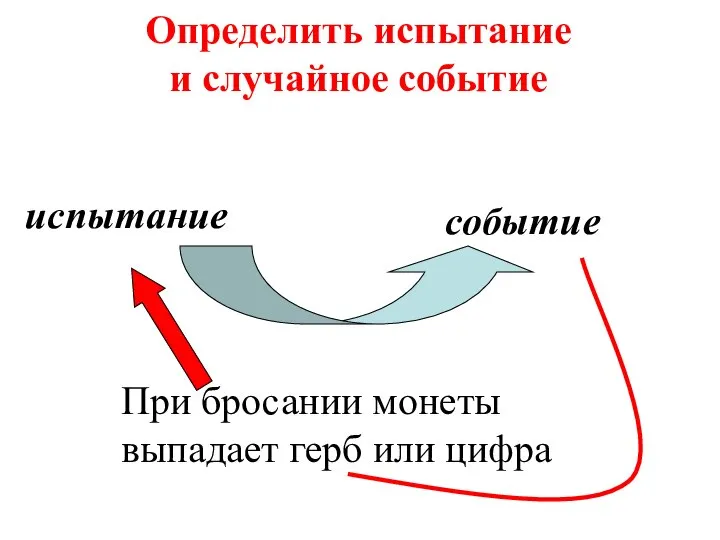
- 10. Определить испытание и случайное событие событие испытание При бросании монеты выпадает герб или цифра
- 11. Виды событий достоверные (обозначение: U) невозможные (обозначение: V) случайные (обозначение: А, В, С и т.д.)
- 12. Невозможные – те, которые в данных условиях произойти не могут. Пример: вода замерзла при t=+20º Достоверные
- 13. Случайные события Пример: светит солнце Пример: прилетел инопланетянин
- 14. Упражнения определите вид события: Любому курсанту 2 курса больше шестнадцати лет. В сборнике задач по высшей
- 15. Упражнения Составьте пример события по картинке и определите его вид: Лиса живет в норе Крокодил солнце
- 16. Виды случайных событий совместные несовместные полная группа событий противоположные равновозможные простые сложные
- 17. Простые событие – это элементарный исход в результате испытания Сложные события – события, состоящие из нескольких
- 18. События бывают: совместные и несовместные Совместные – это события, которые в данных условиях могут происходить одновременно.
- 19. Упражнения определите, события совместные или несовместные: Выпал снег. Начались соревнования по лыжам. Наступил ноябрь. В летнем
- 20. События равновозможные Равновозможные –это те события, которые в данных условиях одинаково возможны. Пример: при подбрасывании монеты
- 21. Упражнения определите, являются ли события равновозможными: 1)При подбрасывании кубика: выпадает число 4 выпадает число 6 2)При
- 22. Противоположным к событию А называют событие , которое происходит, когда не происходит А
- 23. Полная группа событий, если в результате испытания непременно произойдет хотя бы одно из них Полная группа
- 24. Найти среди событий Аi достоверные и невозможные: А1 – «появление 10 очков при бросании игральной кости»;
- 25. 4) Образуют ли полную группу события: испытание – бросание монеты; события: А1 – «появление герба», А2
- 26. Классическое определение вероятности Рассмотрим группу попарно несовместимых событий А1, А2, …, Аn, связанную с некоторым испытанием
- 27. Пусть при бросании игральной кости события А2, А4, А6 - появление соответственно 2, 4 и 6
- 28. Классическое определение вероятности Вычислить вероятность выпадения герба при одном бросании монеты Свойства вероятности Вероятность достоверного события
- 29. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 30. ПРОБЛЕМНЫЙ ВОПРОС 1: А можно ли вычислить вероятность события с помощью ряда экспериментов?
- 31. Опыт человечества Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара. Весь наш
- 32. Частота случайного события Абсолютной частотой случайного события А в серии из N случайных опытов называется число
- 33. Частота случайного события Относительной частотой случайного события называют отношение числа появлений этого события к общему числу
- 34. Примеры Пример 1. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота
- 35. Примеры Пример 2. За лето на Черноморском побережье было 67 солнечных дней. Какова частота солнечных дней
- 36. Примеры Пример 3. Отдел технического контроля обнаружил 5 бракованных изделий в партии из 1000 изделий. Найдите
- 37. Примеры Пример 4. Для выяснения качества семян было отобрано и высеяно в лабораторных условиях 1000 штук.
- 38. ПРОБЛЕМНЫЙ ВОПРОС 2: Может быть, относительную частоту и нужно принять за вероятность?
- 39. Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события
- 40. Проверка Пример 5. Подбрасывание монеты. А – выпадает герб. Классическая вероятность: всего 2 исхода, 1 исход
- 41. Проверка Пример 5. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз, и при этом герб
- 42. Проверка Пример 5. Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз, причем герб выпал 12012
- 43. Результаты Вывод Пример 5 подтверждает естественное предположение о том, что вероятность выпадения герба при одном бросании
- 44. Статистическая вероятность Вероятность случайного события приближенно равна частоте этого события, полученной при проведении большого числа случайных
- 45. Задача №6. Чтобы определить, как часто встречаются в лесопарке деревья разных пород, ребята провели следующие эксперименты.
- 46. Задача №6. Решение: а) A={выбранное наугад в парке дерево - сосна} NА = 315, N =
- 47. По статистике, на каждые 1000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку? Решение: 3/1000
- 48. Демографы утверждают, что вероятность рождения близнецов равна 0,012. В скольких случаях из 10 000 рождений можно
- 49. Основные формулы комбинаторики
- 50. Комбинаторика – это раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества
- 51. Правила сложения и умножения в комбинаторике Правило суммы Если два действия А и В взаимно исключают
- 52. Пример В группе учится 20 юношей и 5 девушек. Сколькими способами можно назначить одного дневального? Решение
- 53. Правило произведения Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе
- 54. Пример. В группе учится 20 юношей и 5 девушек. Сколькими способами можно назначить двух дневальных? Решение
- 55. Размещениями из n различных элементов по m называют комбинации, составленные из данных n элементов по m
- 57. Пример. Группа слушателей второго курса изучает 10 различных дисциплин. Сколькими способами можно составить расписание занятий в
- 58. Перестановками из n различных элементов называют размещения из этих n по n
- 59. Пример. Для лечения заболевания применяют три лекарства. Полагают, что последовательность, в которой принимают лекарства, оказывает существенное
- 60. Сочетаниями из n различных элементов по m называют комбинации, составленные из данных n элементов по m
- 61. Пример. Сколько существует способов выбрать два цветка из корзины, в которой 5 роз и 4 хризантемы?
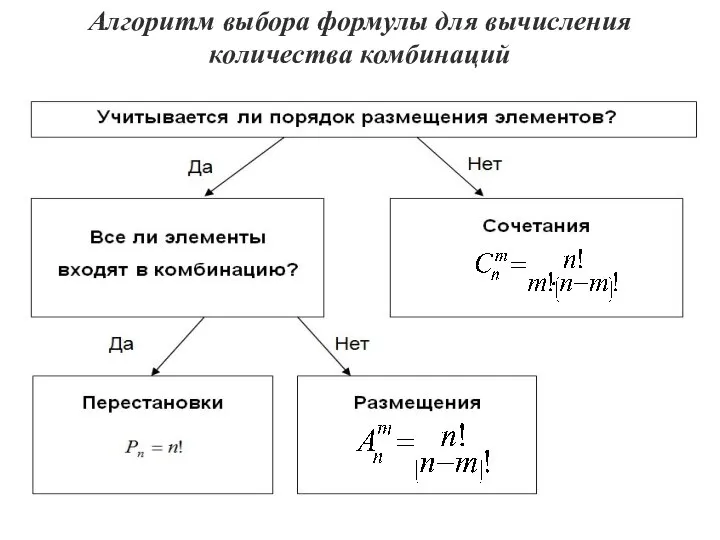
- 62. Алгоритм выбора формулы для вычисления количества комбинаций
- 63. Из трех элементов 2, 5, 6 можно составить по два элемента следующие размещения: (2; 5), (5
- 64. 4. В корзине 3 белых и 2 черных шара. Найти число способов выбора двух шаров, если
- 65. Схема выбора с возвращением Если при упорядоченной выборке m элементов из n элементы возвращаются обратно, то
- 66. Пример. Сколько существует четырёхзначных пин-кодов? По условию задачи нам предложен набор из n = 10 цифр,
- 67. Схема выбора с возвращением Пусть в множестве из n элементов есть m различных типов элементов, при
- 68. Пример. Сколько существует способов расположения шахматных фигур на первой линии шахматной доски? Порядок важен, места на
- 69. Схема выбора с возвращением Если при выборке m элементов из n элементы возвращаются обратно без последующего
- 70. Задача: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? Решение: Так как
- 71. Задача: В кондитерском магазине продавались 4 сорта пирожных: эклеры, песочные, наполеоны и слоеные. Сколькими способами можно
- 72. Задача: Сколькими способами можно переставить буквы слова «ананас»? Решение: всего букв 6. Из них одинаковы n1«а»=3,
- 73. Операции над событиями
- 74. Операции над случайными событиями Суммой А+В = С Испытание – стрельба двух стрелков (каждый делает по
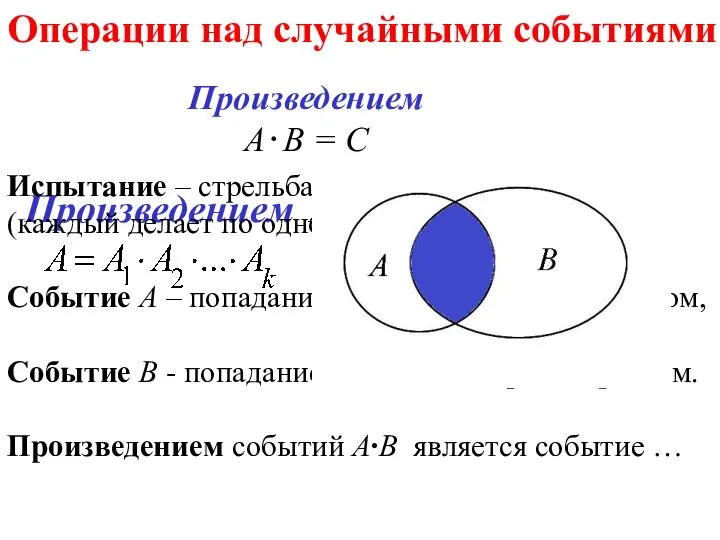
- 75. Операции над случайными событиями Произведением А⋅В = С Произведением Испытание – стрельба двух стрелков (каждый делает
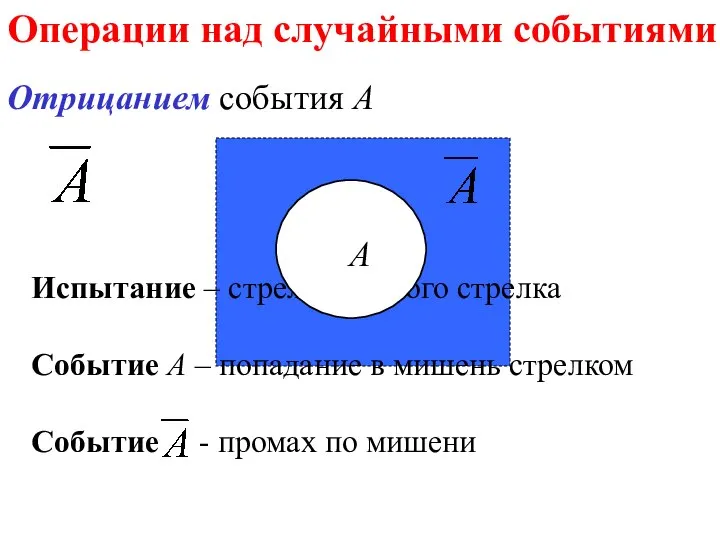
- 76. Операции над случайными событиями Испытание – стрельба одного стрелка Событие А – попадание в мишень стрелком
- 77. Теоремы сложения вероятностей Когда наступит событие С = А + В? А или В или они
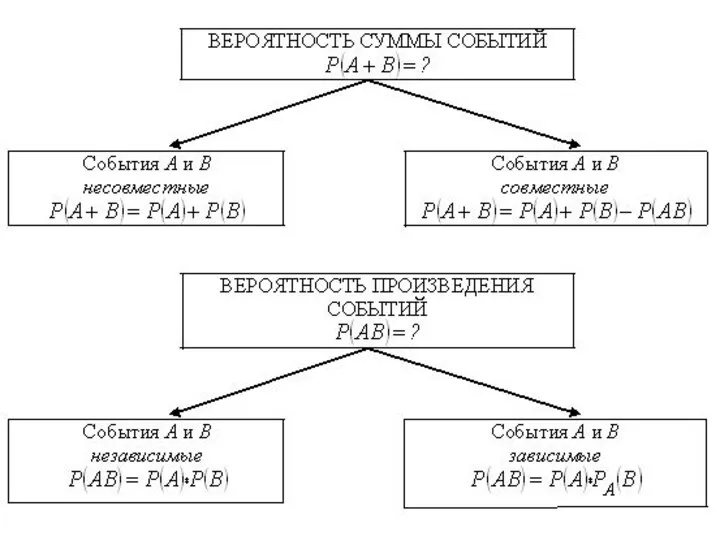
- 78. Теорема Вероятность суммы двух несовместных событий А и В равна …
- 79. Теорема Вероятность суммы конечного числа попарно несовместных событий равна …
- 80. Теорема Вероятность суммы двух совместных событий равна …
- 81. Следствие 1 полная группа попарно несовместных событий Следствие 2
- 82. Пример. В коробке имеется 250 лампочек, из них 100 по 90 Вт, 50 – по 60
- 83. Пример. Два стрелка стреляют в одну и ту же цель, причём вероятность поражения цели первым стрелком
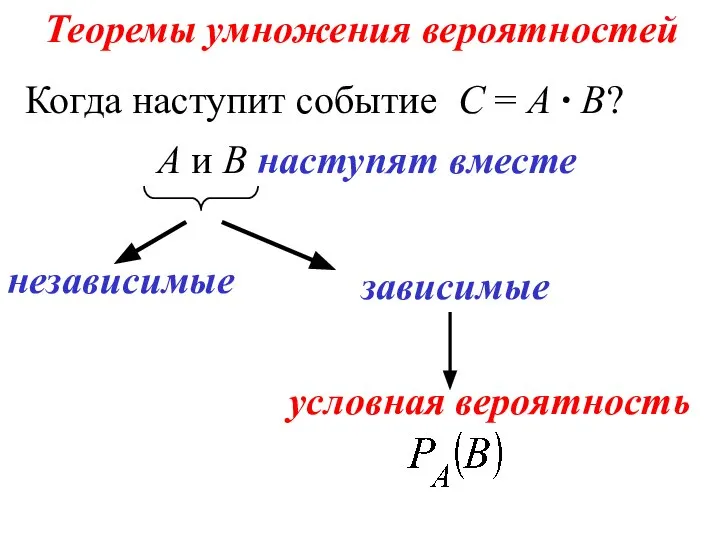
- 84. Теоремы умножения вероятностей Когда наступит событие С = А ∙ В? А и В наступят вместе
- 85. Теорема Вероятность произведения двух зависимых событий А и В равна …
- 86. Теорема Вероятность произведения двух независимых событий равна …
- 90. Брошены 3 игральные кости. Определить вероятность того, что выпадет три «шестерки».
- 91. Круговая мишень состоит из зон с номерами 1, 2, 3. Вероятности попадания в эти зоны при
- 92. Пусть А и В – некоторые события, связанные с одним опытом, причем Р(А) = 0,25 и
- 93. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в 1, 2
- 94. В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из
- 95. Ученик получает оценку от 2 до 5 баллов. Вероятности того, что ему поставят «4», «3» и
- 96. В группе, состоящей из 25 студентов, спортивный разряд по борьбе имеют 10 человек, по стрельбе –
- 97. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,5, вторым 0,
- 98. Формула полной вероятности
- 99. Формула полной вероятности Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из
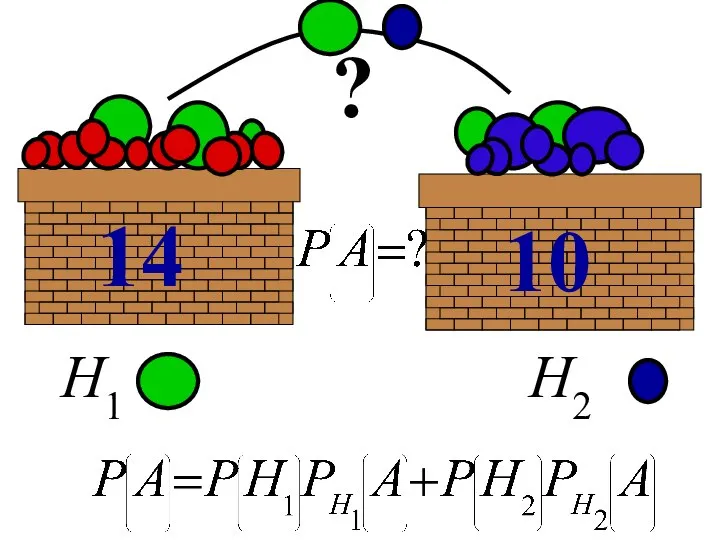
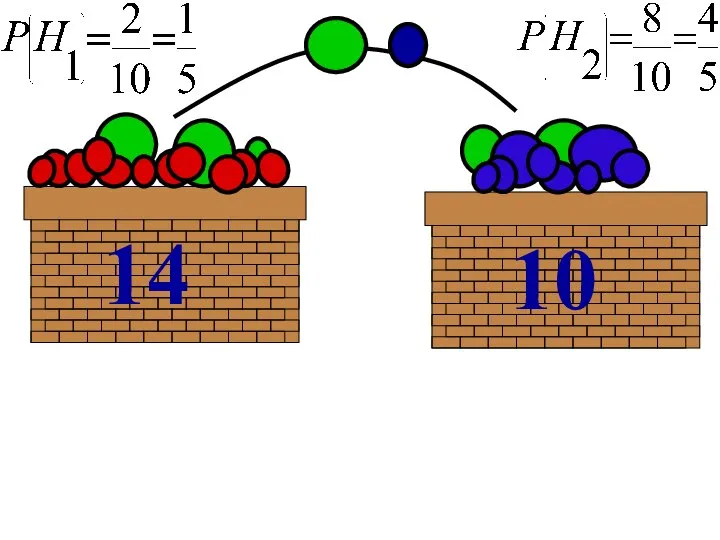
- 100. Пример. В двух корзинах имеются шары. В первой корзине 14 шаров, из них 3 зеленого цвета.
- 101. ? Н1 Н2
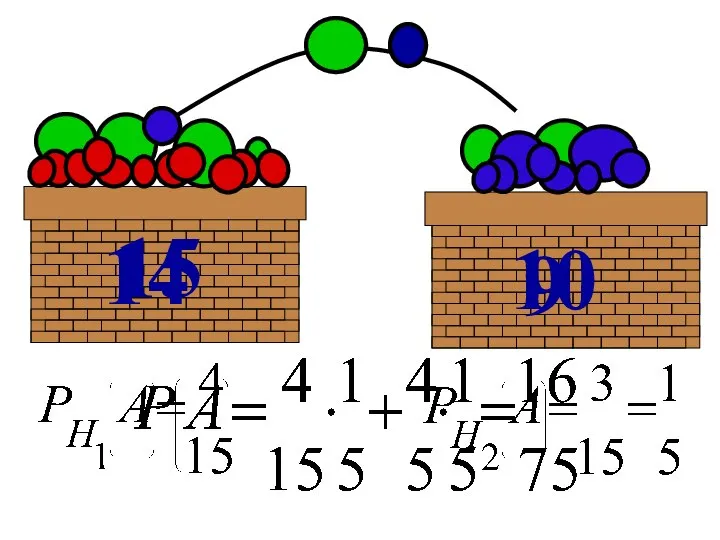
- 103. 14 10 15 9
- 104. Формула Байеса используется для переоценки вероятностей доопытных гипотез. Для оценки вероятности появления некоего события А выдвигают
- 105. Формула Байеса Пусть произведено одно испытание, в результате которого произошло событие А. Как, в связи с
- 106. Пример. Предположим, что 5% мужчин и 0,25% всех женщин имеют рост выше 180 см, наугад выбранное
- 107. Событие А – выбранный человек оказался ростом выше 180 см Гипотеза - выбранный человек мужчина Гипотеза
- 109. а) б)
- 110. Пример. Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов – специалист средней квалификации. Вероятность
- 111. Событие А: Взятый наудачу прибор оказался надёжным. Гипотеза H1 – появление прибора, собранного специалистом высшей квалификации.
- 112. Последовательность независимых испытаний. Формула Бернулли Пусть относительно некоторого случайного события А проводится п испытаний, в одних
- 113. Какова вероятность того, что при этих п испытаниях событие А произойдет т раз? (т – любое
- 114. Пример. Стрелок стреляет по цели пять раз подряд. Вероятность поражения цели этим стрелком при одном выстреле
- 115. Пример Каждый день акции корпорации АВС поднимаются в цене или падают в цене на один пункт
- 116. Случайное событие качественная характеристика испытания количественная характеристика испытания Случайная величина Случайной величиной называется величина, которая может
- 117. Случайные величины Случайная дискретная величина - это такая величина ,число возможных испытаний которой либо конечно, либо
- 118. Примеры ДСВ 1. Частота попаданий при 3 выстрелах – X x1=0, x2=1, x3=2, x4=3 2. Игрок
- 119. Примеры ДСВ 3. Эксперимент – одновременное бросание двух игральных кубиков, случайная величина – сумма выпавших очков,
- 120. Случайные величины Случайной непрерывной величиной называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал (конечный
- 121. Примеры НСВ 1. Случайное отклонение по дальности точки падения снаряда от цели 2. Продолжительность работы электрической
- 122. Числовые характеристики ДСВ
- 123. Математическое ожидание Д.С.В.
- 124. Теорема. Свойства математического ожидания Д.С.В.
- 126. независимые
- 127. Теорема. М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность
- 128. ? отклонение значений случайной величины от М(Х) Дисперсия С.В.
- 129. Свойства дисперсии Д.С.В.
- 130. Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р
- 131. Способы вычисления дисперсии Д.С.В.
- 132. Законы распределения ДСВ
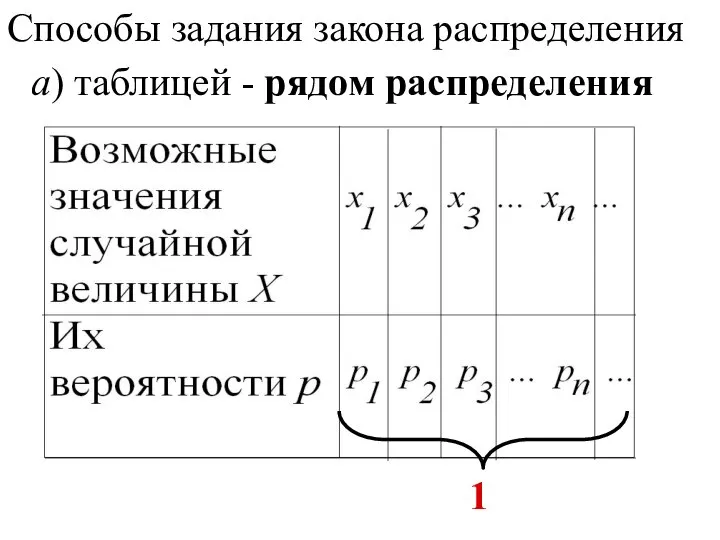
- 133. 1 Способы задания закона распределения а) таблицей - рядом распределения
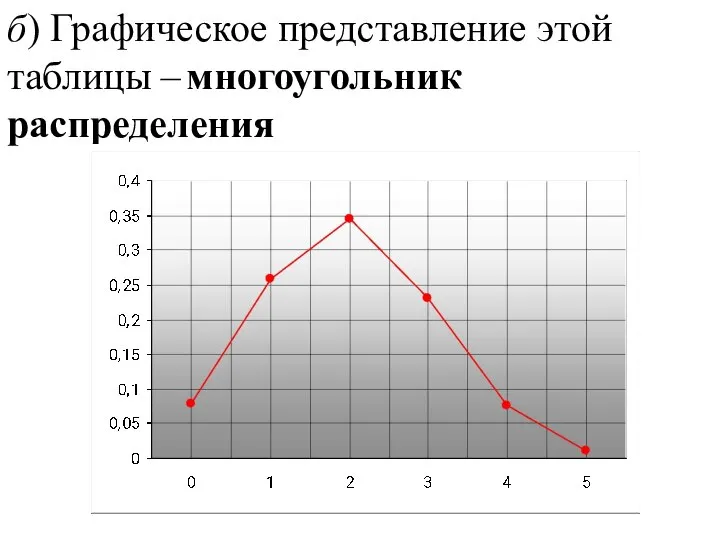
- 134. б) Графическое представление этой таблицы – многоугольник распределения
- 135. Законы распределения ДСВ 1.Биноминальный закон распределения 2. Закон распределения Пуассона р ≤ 0,1
- 136. Числовые характеристики НСВ
- 137. Математическое ожидание Н.С.В. Дисперсия Н.С.В.
- 138. Среднее квадратичное отклонение Модой (М0) Д.С.В. называется ее наиболее вероятное значение Модой (М0) Н.С.В. называется такое
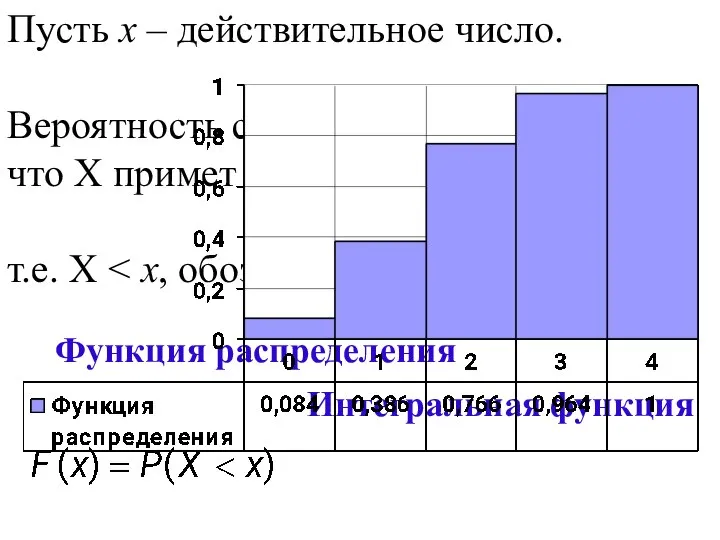
- 139. Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х,
- 140. плотность распределения вероятности Н.С.В. Х Свойства плотности распределения
- 141. Законы распределения Н.С.В. Равномерное распределение на отрезке [a, b]
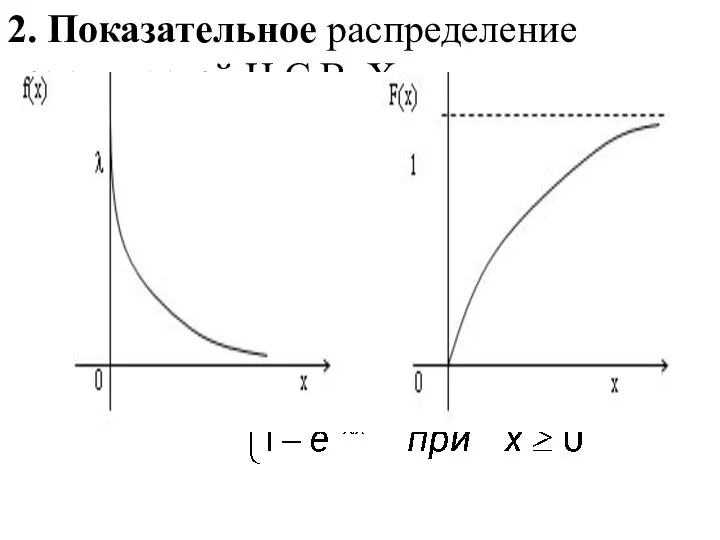
- 142. 2. Показательное распределение вероятностей Н.С.В. Х λ - положительное число
- 143. 3. Нормальный закон распределения
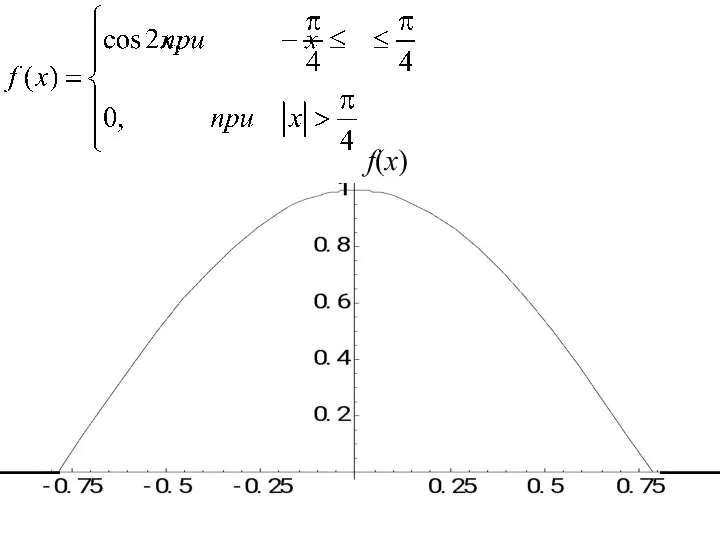
- 144. Пример. Задана Н.С.В. Х своей плотностью распределения f(x).
- 145. 1. Определить коэффициент А. 2. Найти функцию распределения. 3. Построить графики функции распределения и плотности распределения.
- 146. Найдем коэффициент А
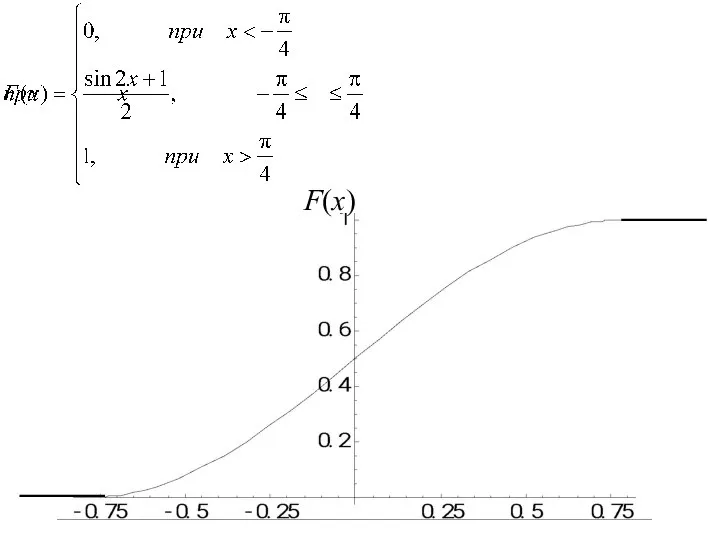
- 149. Найдем функцию распределения :
- 150. 1) На участке :
- 151. 2) На участке :
- 152. 3) На участке :
- 153. :
- 154. :
- 155. :
- 156. : Найдем вероятность попадания случайной величины в интервал
- 157. : Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х
- 158. :
- 162. Скачать презентацию
































































































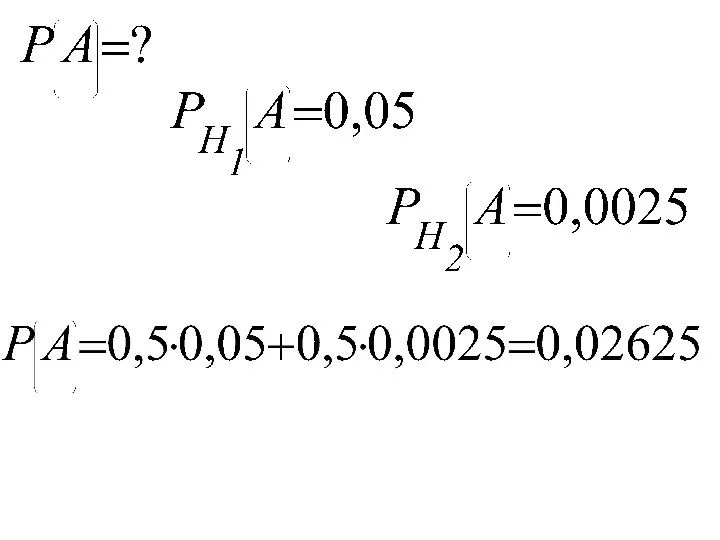
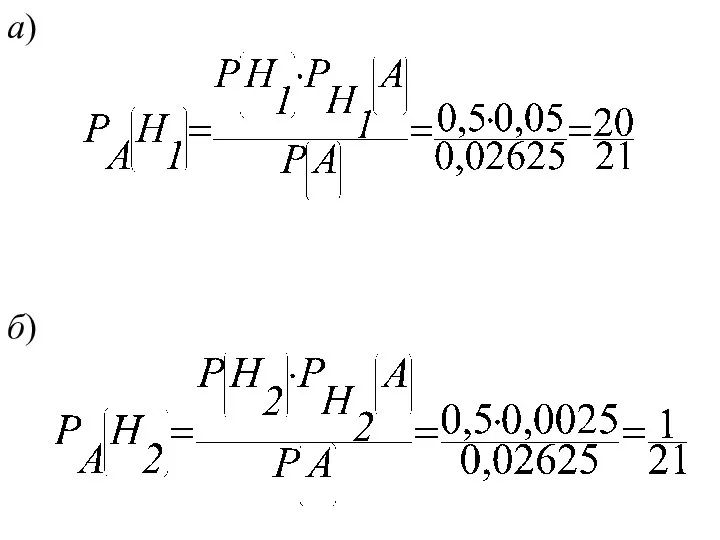















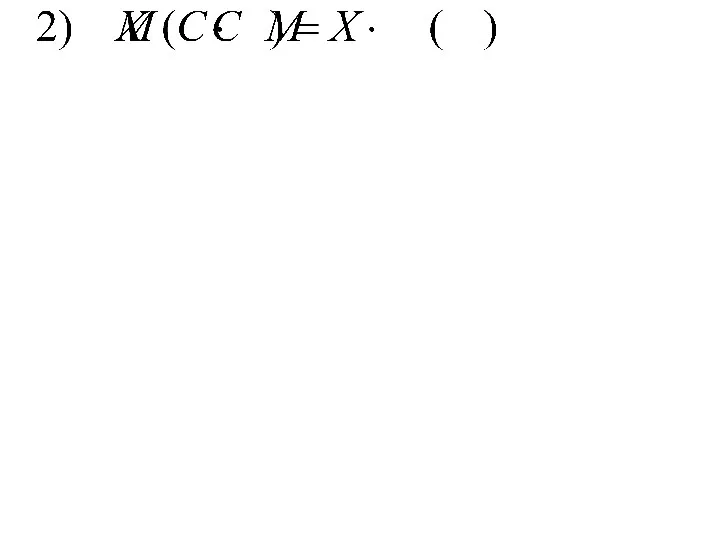
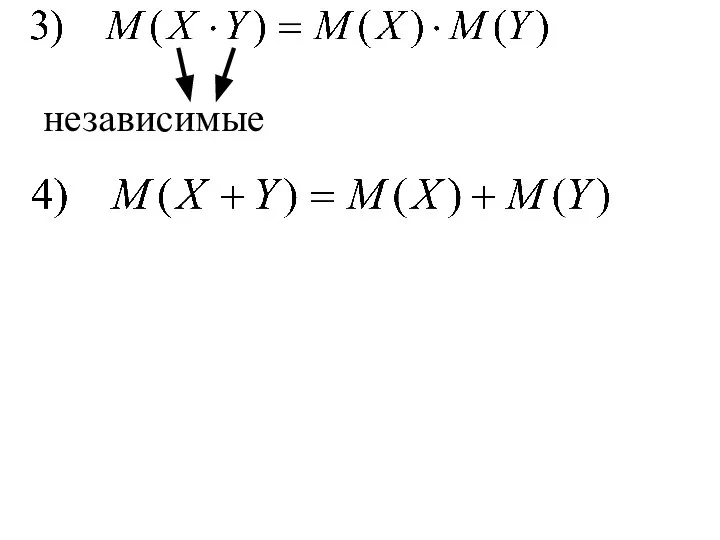








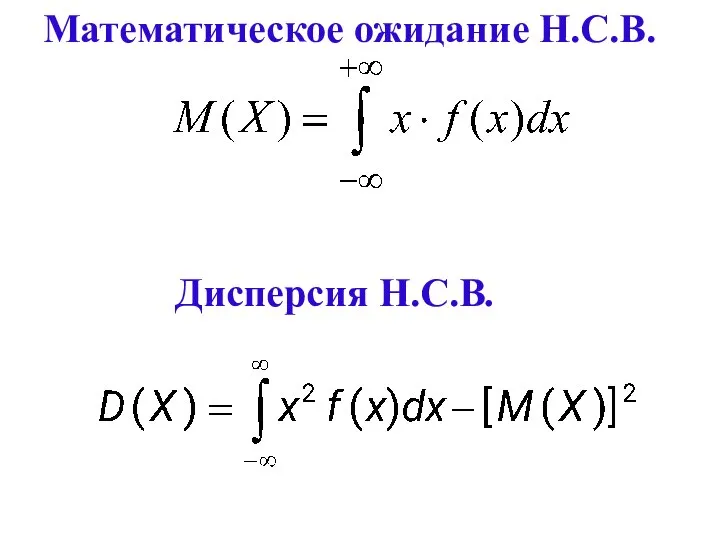


![Законы распределения Н.С.В. Равномерное распределение на отрезке [a, b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1138304/slide-140.jpg)




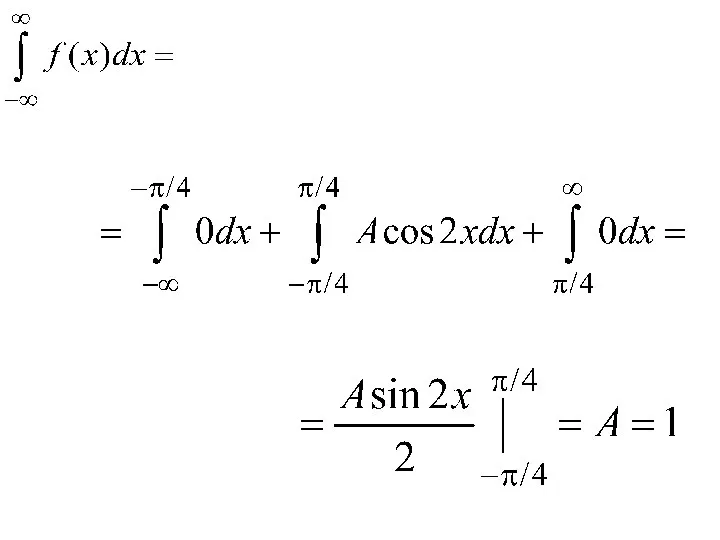
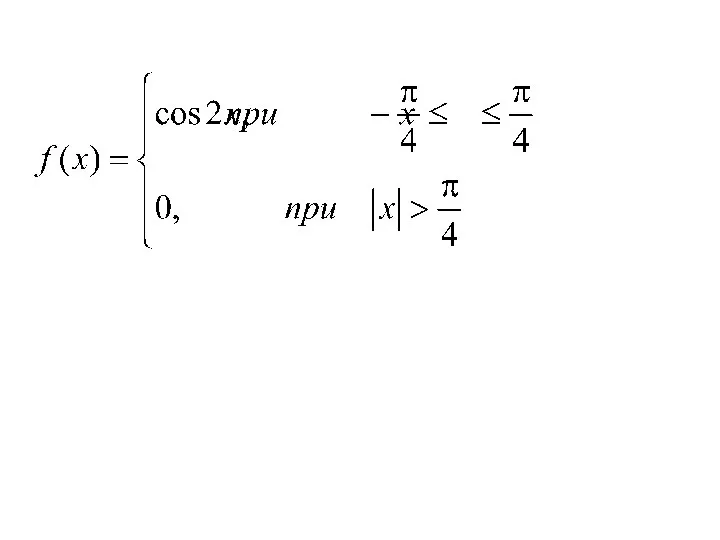

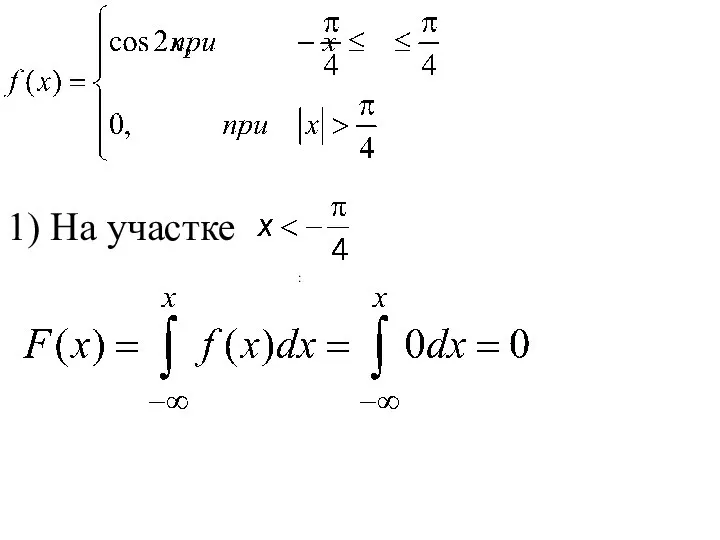
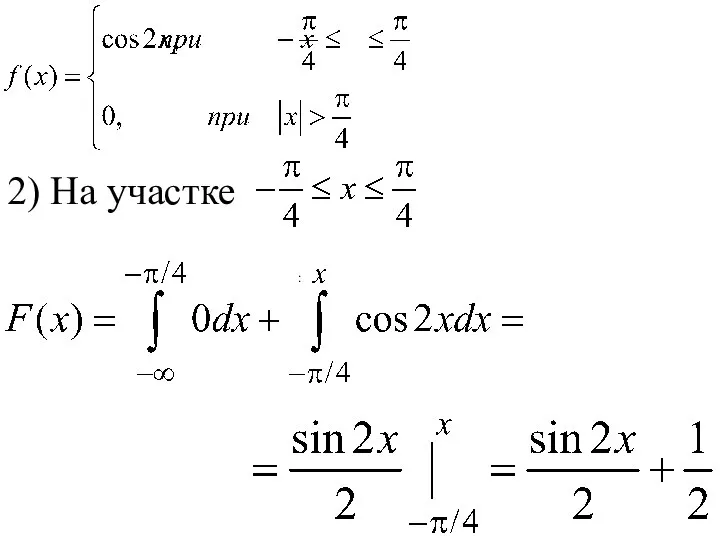
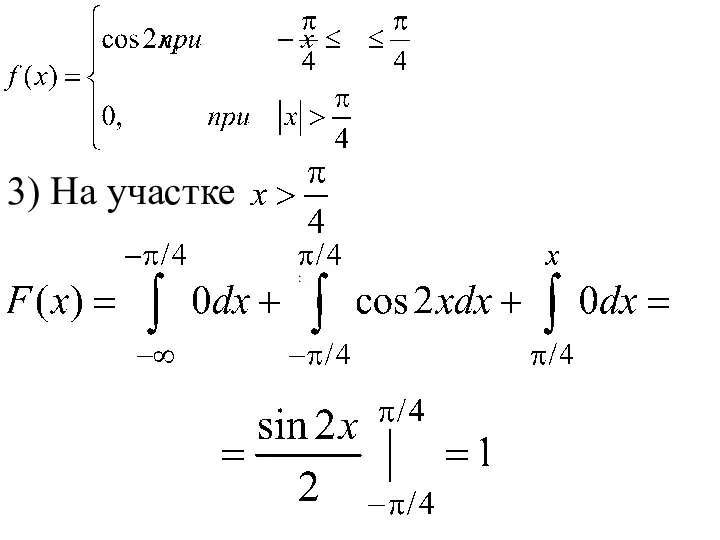
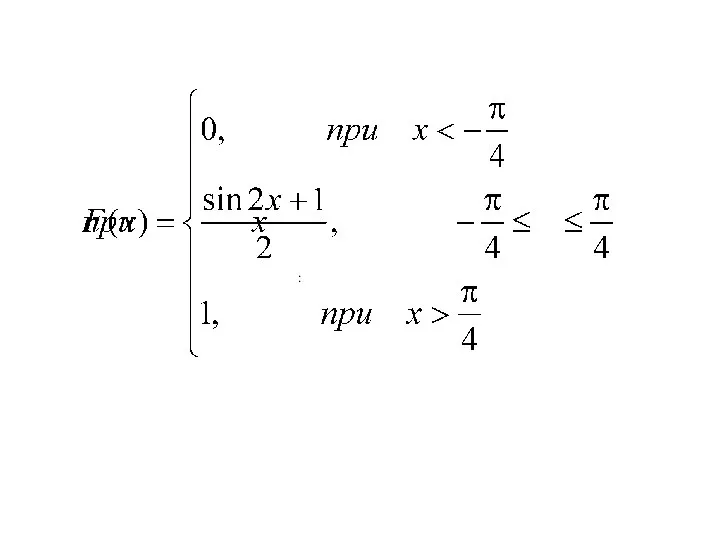


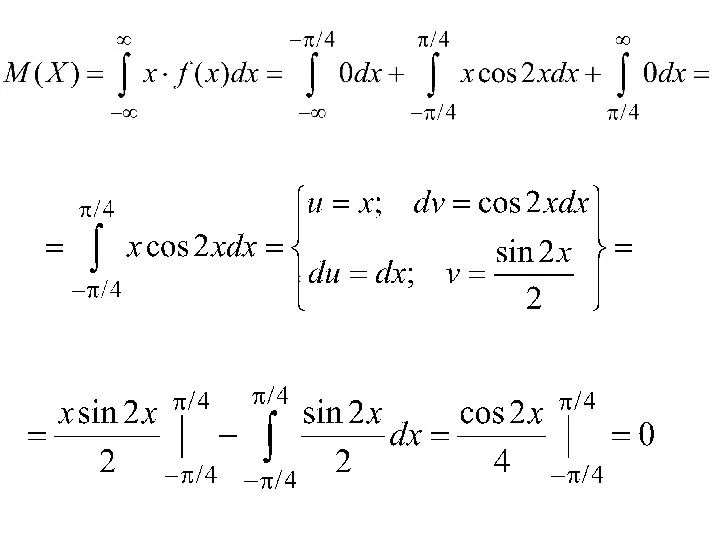
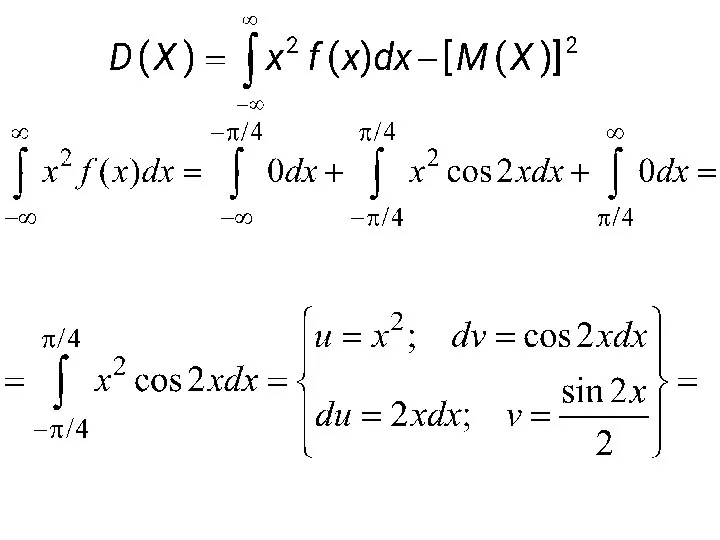
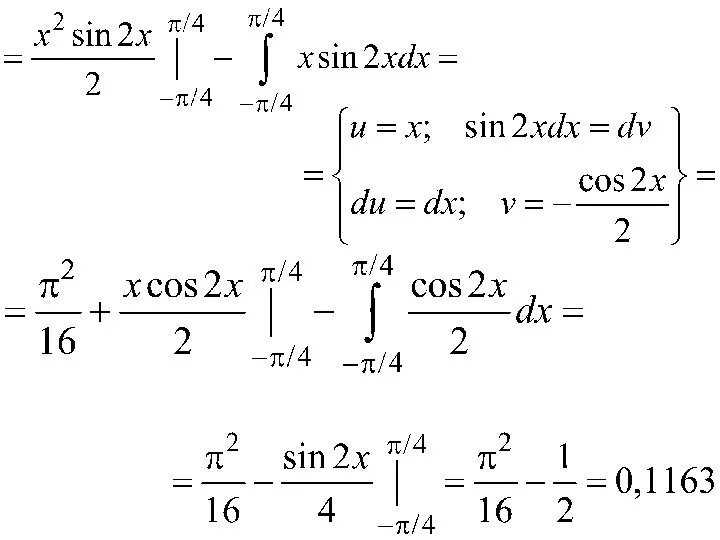
 Математическое моделирование. Лекция 1
Математическое моделирование. Лекция 1 Проектирование последовательностных схем
Проектирование последовательностных схем Один и много
Один и много Параллельные прямые в пространстве
Параллельные прямые в пространстве Математическая модель игры World of Tanks
Математическая модель игры World of Tanks Презентация на тему Уравнения
Презентация на тему Уравнения 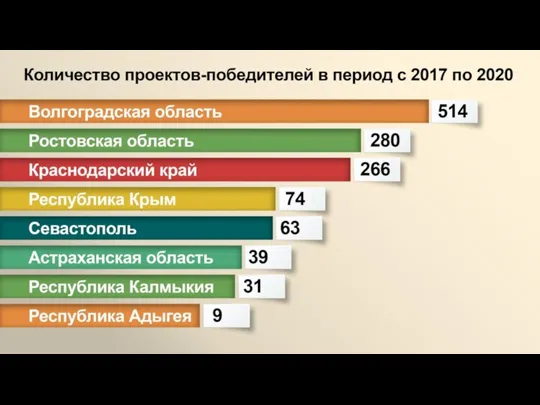 Количество проектов-победителей в период с 2017 по 2020 гг
Количество проектов-победителей в период с 2017 по 2020 гг Обратные тригонометрические функции и их свойства
Обратные тригонометрические функции и их свойства Интеллектуальная игра Самый умный. Информатика. Математика
Интеллектуальная игра Самый умный. Информатика. Математика Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Деление обыкновенных дробей
Деление обыкновенных дробей Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3
Интегрированный урок математики и краеведения. Путешествие по Кизильскому району. Часть 3 Примеры задач с таблицами истинности
Примеры задач с таблицами истинности Таблица умножения
Таблица умножения Истинностные задачи
Истинностные задачи Чётные и нечётные функции
Чётные и нечётные функции Статистика и ее роль в развитии общества
Статистика и ее роль в развитии общества Запись Арифметических выражений и на языке программирования Паскаль
Запись Арифметических выражений и на языке программирования Паскаль Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Задачи ФИПИ
Задачи ФИПИ Первый признак параллельности прямых
Первый признак параллельности прямых Математика
Математика Цена деления измерительных приборов
Цена деления измерительных приборов Свойства степеней с натуральными показателями
Свойства степеней с натуральными показателями Производная в экономике
Производная в экономике Вынесение множителя из - под знака корня. Внесение множителя под знак корня
Вынесение множителя из - под знака корня. Внесение множителя под знак корня Алгебра в жизни человека
Алгебра в жизни человека