Содержание
- 2. Отношения Упорядоченные наборы Произведение множеств Бинарные отношения Представление отношений Функциональные отношения Отношения эквивалентности Отношения порядка Вопросы
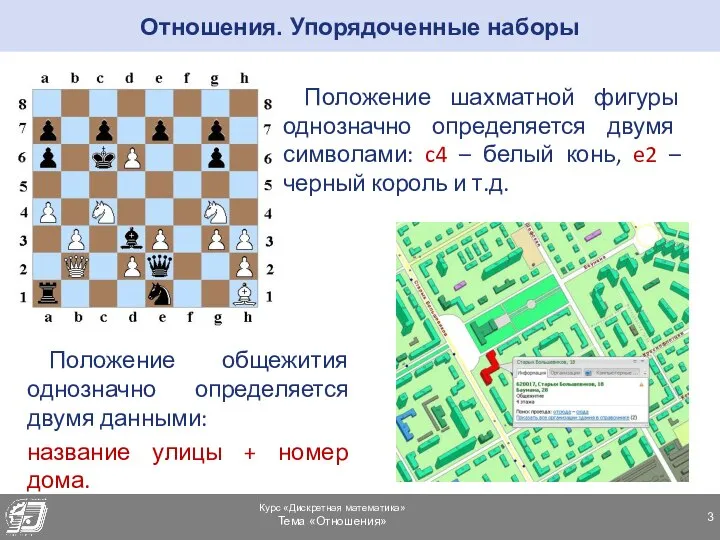
- 3. Отношения. Упорядоченные наборы Положение шахматной фигуры однозначно определяется двумя символами: c4 – белый конь, e2 –
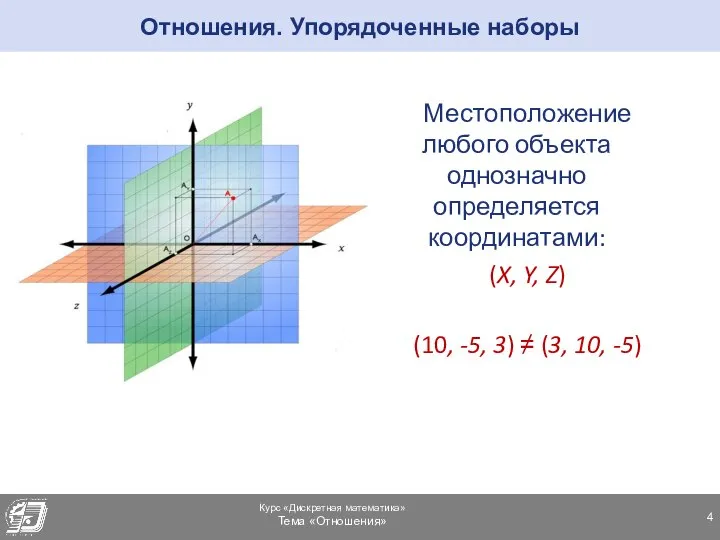
- 4. Отношения. Упорядоченные наборы Местоположение любого объекта однозначно определяется координатами: (X, Y, Z) (10, -5, 3) ≠
- 5. Отношения. Упорядоченные наборы Данные о человеке однозначно определяются: Фамилия Имя Отчество Дата рождения (чч.мм.гггг) Место рождения
- 6. Отношения. Упорядоченные наборы Упорядоченный набор (кортеж, n-ка) данных – последовательность из n объектов a1, a2,… ,
- 7. Отношения. Прямое произведение множеств Прямое произведение множеств A 1, A 2, … , A n есть
- 8. Отношения. Прямое произведение множеств Теорема: Для конечных множеств A и B |A×B|=|A|×|B|. Лемма: (A × B)
- 9. Бинарные отношения Бинарным отношением между множествами A и B называется подмножество R прямого произведения A ×
- 10. Бинарные отношения Пример: Семья Weasley. Отношение R = {(x, y)| x – отец y }. Тогда
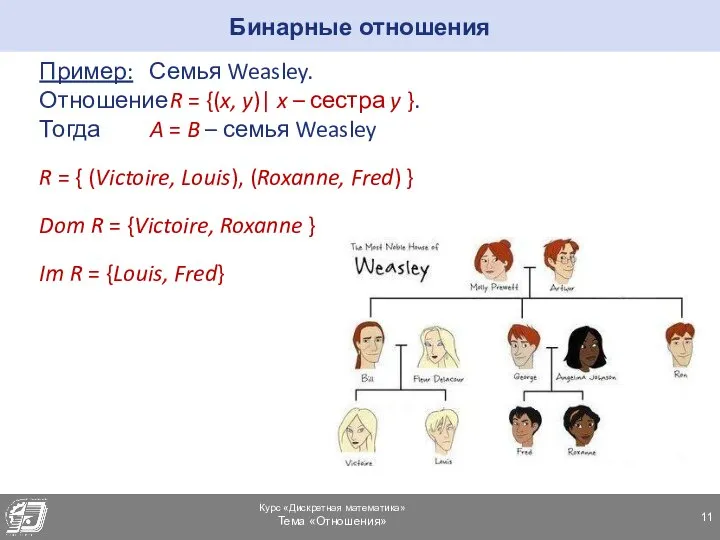
- 11. Бинарные отношения Пример: Семья Weasley. Отношение R = {(x, y)| x – сестра y }. Тогда
- 12. Бинарные отношения Особые виды отношений Пусть R - отношение между множествами A и B. Обратное отношение
- 13. Операции над отношениями Отношение – это некоторое множество ⟹ допустимы все теоретико-множественные операции Пример: ℕ -
- 14. Композиция отношений Пусть R1 : A → B и R2 : B → C. Композиция отношений
- 15. Бинарные отношения Свойства отношений Пусть R - отношение на множестве A. Рефлексивность ∀x ∈ A ⇒
- 16. Бинарные отношения Свойства отношений Теорема: Если R ⊂ A2 - отношение на множестве А, то R
- 17. Представление отношений прямым перечислением всех пар в виде графа графиком матрицей (машинное представление) Пусть R ⊂
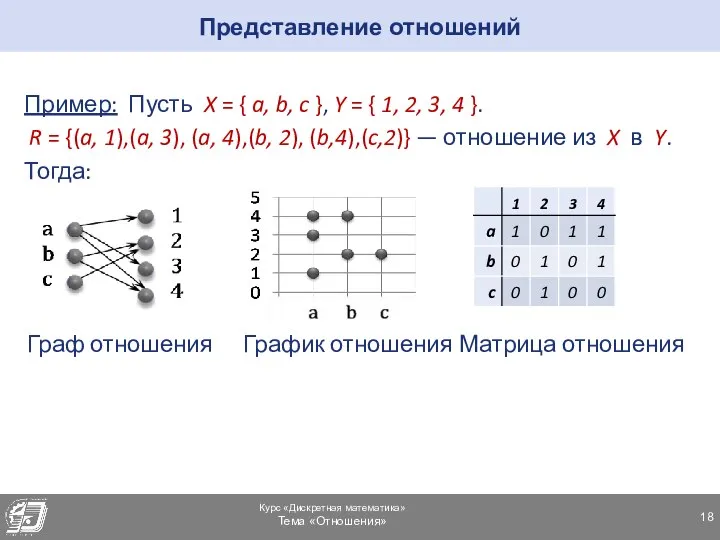
- 18. Представление отношений Пример: Пусть X = { a, b, c }, Y = { 1, 2,
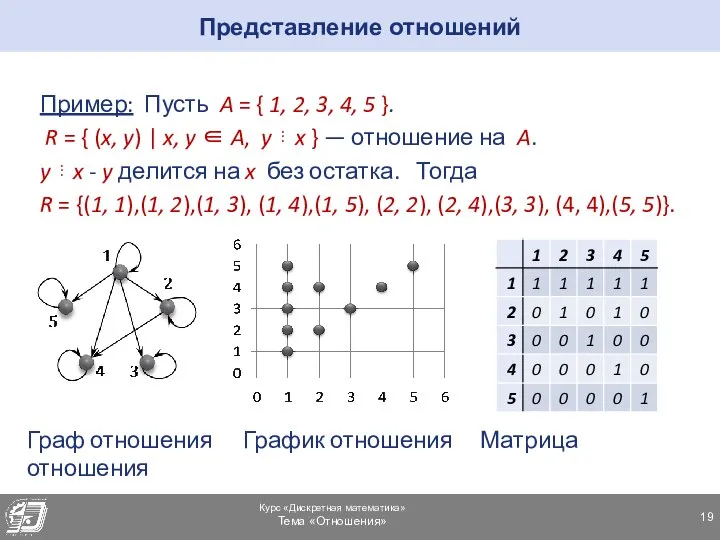
- 19. Представление отношений Пример: Пусть A = { 1, 2, 3, 4, 5 }. R = {
- 20. Пусть f - отношение между множествами A и B. Отношение называется функциональным (функцией), если ∀x ∈
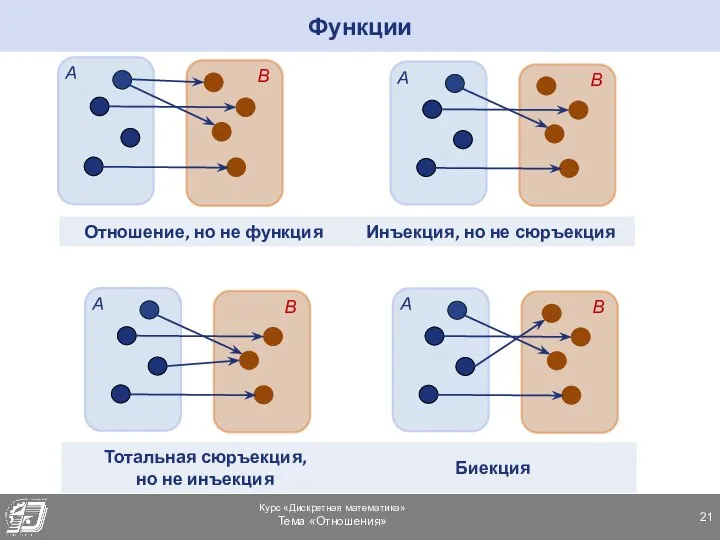
- 21. Функции
- 22. Теорема: Если f : A → B - тотальная биекция, то отношение f-1 ⊂ B ×
- 23. Композиция функций называется суперпозицией Обозначение: если f : A → B и g : B →
- 24. Отношения эквивалентности Отношение эквивалентности – рефлексивное, симметричное, транзитивное отношение. Если R - отношение эквивалентности, то говорят,
- 25. Отношения эквивалентности Теорема: отношение эквивалентности на некотором множестве A порождает его разбиение на классы эквивалентности –
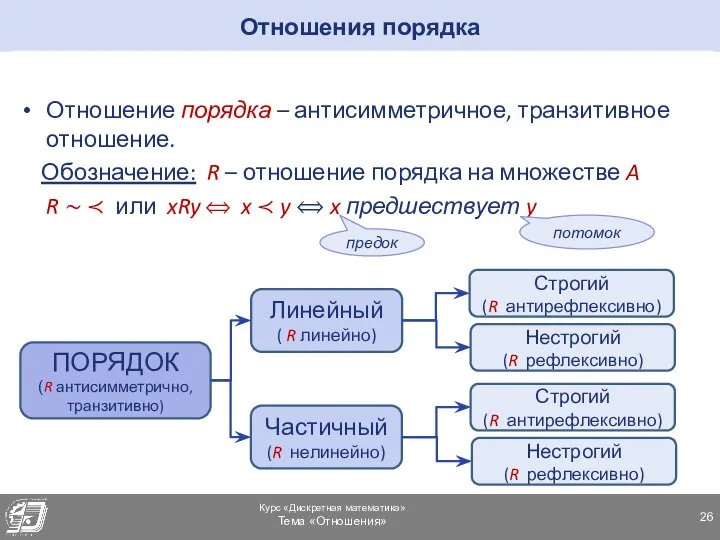
- 26. Отношения порядка Отношение порядка – антисимметричное, транзитивное отношение. Обозначение: R – отношение порядка на множестве A
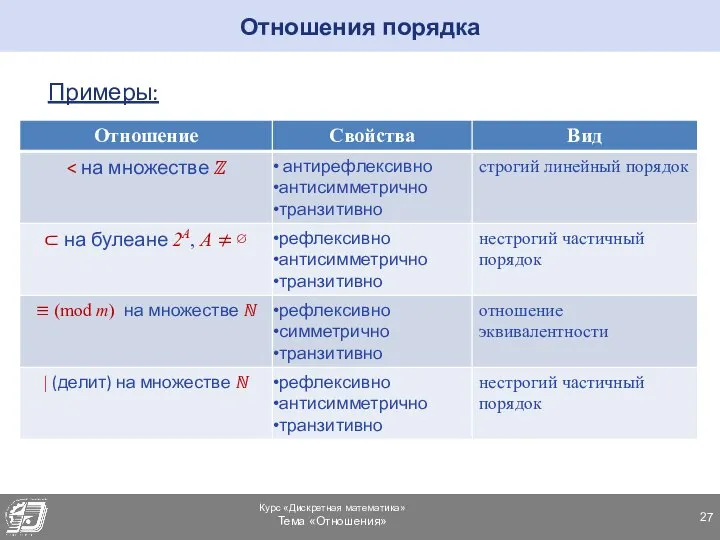
- 27. Отношения порядка Примеры:
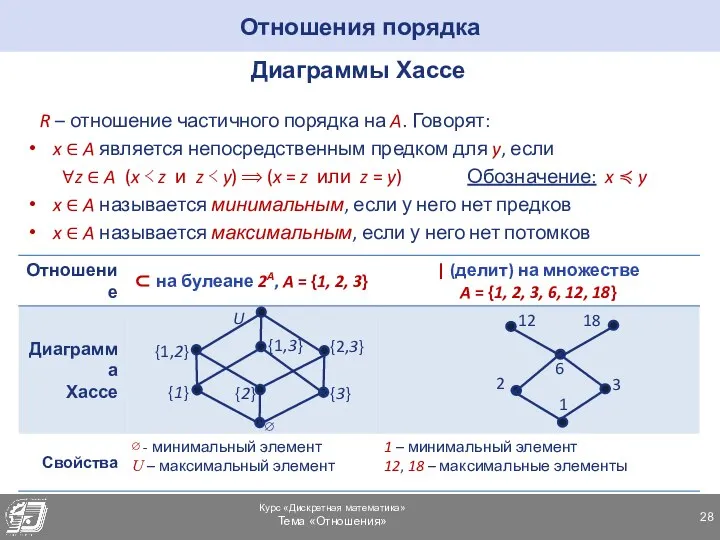
- 28. Отношения порядка Диаграммы Хассе R – отношение частичного порядка на A. Говорят: x ∈ A является
- 30. Скачать презентацию


















 Интенсив ЦОКО по математике
Интенсив ЦОКО по математике Презентация на тему Почему нельзя жить без математики?
Презентация на тему Почему нельзя жить без математики?  Презентация на тему Натуральные логарифмы
Презентация на тему Натуральные логарифмы  Площадь многоугольников. Решение задач
Площадь многоугольников. Решение задач Деление на 3
Деление на 3 Решение логарифмических неравенств
Решение логарифмических неравенств Устный счёт
Устный счёт Задачи на построение угла
Задачи на построение угла Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 16
Решение линейных неравенств с одной переменной. Числовые промежутки. Урок 16 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Вычисление определенных интегралов
Вычисление определенных интегралов Квадратичная функция у=х2 и ее свойства
Квадратичная функция у=х2 и ее свойства Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Односторонние пределы
Односторонние пределы Математика с котом Леопольдом
Математика с котом Леопольдом Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана
Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана Презентация на тему Числовые промежутки
Презентация на тему Числовые промежутки  Алгоритм исследования функции одного аргумента
Алгоритм исследования функции одного аргумента Задачи на призму
Задачи на призму Метод Гаусса
Метод Гаусса Генеральная средняя
Генеральная средняя Анализ контрольной работы по геометрии
Анализ контрольной работы по геометрии теорема Виета
теорема Виета Криволинейные интегралы
Криволинейные интегралы Случайные события. Вероятности и частоты
Случайные события. Вероятности и частоты Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Презентация на тему Теорема о сумме углов треугольника
Презентация на тему Теорема о сумме углов треугольника  Приёмы вычитания с переходом через десяток
Приёмы вычитания с переходом через десяток