Диаграммы. Matplotlib ч. 2

Столбчатые диаграммы
Для визуализации категориальных данных хорошо подходят столбчатые диаграммы. Для их построения используются функции:
• bar() - вертикальная столбчатая диаграмма;
• barh() - горизонтальная столбчатая диаграмма.

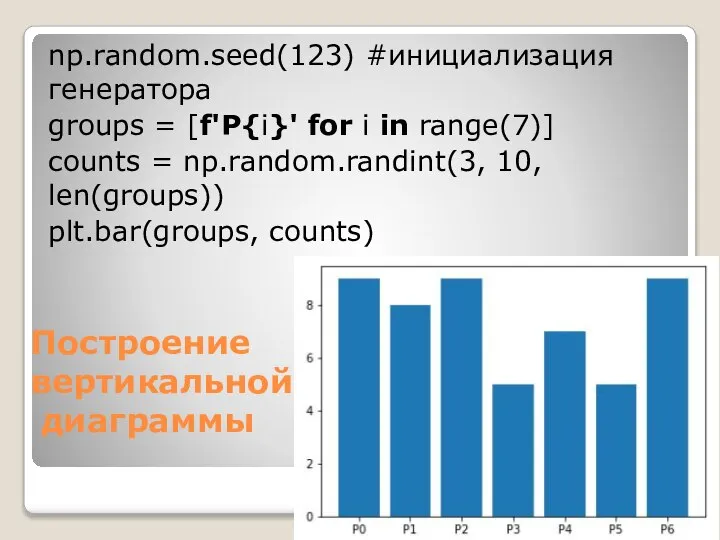
Построение
вертикальной
диаграммы
np.random.seed(123) #инициализация генератора
groups = [f'P{i}' for i in range(7)]
counts = np.random.randint(3, 10, len(groups))
plt.bar(groups, counts)

Параметры функции bar():
Основные параметры:
• x: массив
◦ x-координаты столбцов.
• height : скалярная величина или массив
◦ Высоты столбцов.
• width: скалярная величина, массив или optional
◦ Ширина столбцов.
• bottom: скалярная величина, массив или optional
◦ y-координата базы.
• align: {'center', 'edge'}, optional; значение по умолчанию:
'center'
◦ Выравнивание по координате x.

Дополнительные параметры:
• color: скалярная величина, массив или optional
◦ Цвет столбцов диаграммы.
• edgecolor: скалярная величина, массив или optional
◦ Цвет границы столбцов.
• linewidth: скалярная величина, массив или optional
◦ Ширина границы.
• tick_label: str, массив или optional
◦ Метки для столбца.
• xerr, yerr: скалярная величина, массив размера shape(N,),
shape(2, N) или optional
◦ Величина ошибки для графика.
• ecolor: скалярная величина, массив или optional; значение по умолчанию: 'black'
◦ Цвет линии ошибки.
• log: bool, optional; значение по умолчанию: False
◦ Включение логарифмического масштаба для оси y.
• orientation: {'vertical', 'horizontal'}, optional
◦ Ориентация: вертикальная или горизонтальная.

Выставленное значение
прибавляется/удаляется к верхней (правой - для
горизонтального графика) границе. Может принимать
следующие значения:
▪ скаляр: симметрично +/- для всех баров;
▪ shape(N,): симметрично +/- для каждого бара;
▪ shape(2,N): выборочного - и + для каждого бара. Первая
строка содержит нижние значения ошибок, вторая строка —
верхние;
▪ None: не отображать значения ошибок. Это значение
используется по умолчанию.

Пример, демонстрирующий работу с параметрами bar():
import matplotlib.colors as mcolors
bc = mcolors.BASE_COLORS
np.random.seed(123)
groups = [f'P{i}' for i in range(7)]
counts = np.random.randint(0, len(bc), len(groups))
width = counts*0.1
colors = [['r', 'b', 'g'][int(np.random.randint(0, 3, 1))] for _ in counts]
plt.bar(groups, counts, width=width, alpha=0.6, bottom=2, color=colors,
edgecolor='k', linewidth=2)

numpy.random.randint
numpy.random.randint(low, high=None, size=None, dtype='l')
Массив случайных целых чисел из интервала [low; high). Если параметр high не указан, то значения берутся из интервала [0, low).
Чсла берутся из дискретного равномерного распределения.
Параметры:
low - целое число Определяет нижнюю границу интервала [low; high), из которого возвращаются случайные значения. Если параметр high не указан, то параметр low определяет верхнюю границу интервала [0, low).
high - целое число, необязательный параметр Определяет верхнюю границу интервала [low; high), из которого возвращаются случайные значения
size - целое положительное число или кортеж целых положительных чисел, необязательный параметр Если данный параметр не указан, то будет возвращено одно целое случайное число. Если указано одно число d, то будет возвращен одномерный массив с количеством элементов равным d.

Групповые столбчатые диаграммы
Используя определенным образом подготовленные данные можно
строить групповые диаграммы:
cat_par = [f'P{i}' for i in range(5)]
g1 = [10, 21, 34, 12, 27]
g2 = [17, 15, 25, 21, 26]
width = 0.3
x = np.arange(len(cat_par))
fig, ax = plt.subplots()
rects1 = ax.bar(x - width/2, g1, width, label='g1')
rects2 = ax.bar(x + width/2, g2, width, label='g2')
ax.set_title('Пример групповой диаграммы')
ax.set_xticks(x)
ax.set_xticklabels(cat_par)
ax.legend()

Диаграмма с errorbar элементом
Errorbar элемент позволяет задать величину ошибки для каждого элемента графика.
Для этого используются параметры xerr, yerr и ecolor, первые два определяют величину ошибки, последний – цвет.

Диаграмма с errorbar элементом
np.random.seed(123)
rnd = np.random.randint
cat_par = [f'P{i}' for i in range(5)]
g1 = [10, 21, 34, 12, 27]
error = np.array([[rnd(2,7),rnd(2,7)] for _ in range(len(cat_par))]).T
fig, axs = plt.subplots(1, 2, figsize=(10, 5))
axs[0].bar(cat_par, g1, yerr=5, ecolor='r', alpha=0.5, edgecolor='b', linewidth=2)
axs[1].bar(cat_par, g1, yerr=error, ecolor='r', alpha=0.5, edgecolor='b',
linewidth=2)

Классическая круговая диаграмма
Для построения круговых диаграмм в Matplotlib используется функция pie().
Пример построения диаграммы:
vals = [24, 17, 53, 21, 35]
labels = ['Ford', 'Toyota', 'BMV', 'AUDI', 'Jaguar']
fig, ax = plt.subplots()
ax.pie(vals, labels=labels)
ax.axis('equal')

Параметры функции pie():
• x: массив
◦ Массив с размерами долей.
• explode: массив, optional; значение по умолчанию: None
◦ Если параметр не равен None, то часть долей, которые перечислены в передаваемом значении, будут вынесены из диаграммы на заданное расстояние
• labels: list, optional; значение по умолчанию: None
◦ Текстовые метки долей.
• colors: массив, optional; значение по умолчанию: None
◦ Цвета долей.

Параметры функции pie():
• autopct: str, функция, optional; значение по умолчанию: None
◦ Формат текстовой метки внутри доли, текст - это численное
значение показателя, связанного с конкретной долей.
• pctdistance: float, optional; значение по умолчанию: 0.6
◦ Расстояние между центром каждой доли и началом текстовой
метки, которая определяется параметром autopct.
• shadow: bool, optional, значение по умолчанию: False
◦ Отображение тени для диаграммы.
• labeldistance: float, None, optional; значение по умолчанию: 1.1
◦ Расстояние, на котором будут отображены текстовые метки
долей. Если параметр равен None, то метки не будет отображены.

Параметры функции pie():
• startangle: float, optional; значение по умолчанию: None
◦ Задает угол, на который нужно повернуть диаграмму против
часовой стрелки относительно оси x.
• radius: float, optional; значение по умолчанию: None
◦ Величина радиуса диаграммы.
• counterclock: bool, optional; значение по умолчанию: True
◦ Определяет направление вращения: по часовой или против
часовой стрелки.
• wedgeprops: dict, optional; значение по умолчанию: None
◦ Словарь параметров, определяющих внешний вид долей (см. класс matplotlib.patches.Wedge).

Параметры функции pie():
• textprops: dict, optional; значение по умолчанию: None
◦ Словарь параметров, определяющих внешний вид текстовых
меток (см. класс matplotlib.text.Text).
• center: list значений float, optional; значение по умолчанию:
(0, 0)
◦ Центр диаграммы.
• frame: bool, optional; значение по умолчанию: False
◦ Если параметр равен True, то вокруг диаграммы будет
отображена рамка.
• rotatelabels: bool, optional; значение по умолчанию: False
◦ Если параметр равен True, то текстовые метки будут повернуты
на заданный угол.

Пример, демонстрирующий работу с параметрами функции pie():
vals = [24, 17, 53, 21, 35]
labels = ['Ford', 'Toyota', 'BMV', 'AUDI','Jaguar']
explode = (0.1, 0, 0.15, 0, 0)
fig, ax = plt.subplots()
ax.pie(vals, labels=labels, autopct='%1.1f%%', shadow=True,explode=explode,wedgeprops={'lw':1, 'ls':'--','edgecolor':'k'},
rotatelabels=True)
ax.axis('equal')

Вложенные круговые диаграммы
Вложенная круговая диаграмма состоит из двух компонент: внутренняя ее часть является детальным представлением информации, а внешняя - суммарной по заданным областям. Каждая область представляет собой список численных значений, вместе они образуют общий набор данных.

Пример:
fig, ax = plt.subplots()
offset=0.4
data = np.array([[5, 10, 7], [8, 15, 5], [11, 9, 7]])
cmap = plt.get_cmap('tab20b')
b_colors = cmap(np.array([0, 8, 12]))
sm_colors = cmap(np.array([1, 2, 3, 9, 10, 11, 13, 14, 15]))
ax.pie(data.sum(axis=1), radius=1, colors=b_colors,
wedgeprops=dict(width=offset, edgecolor='w'))
ax.pie(data.flatten(), radius=1-offset, colors=sm_colors,
wedgeprops=dict(width=offset, edgecolor='w'))

Круговая диаграмма с отверстием
Это можно сделать через параметр wedgeprops, который отвечает за внешний вид долей:
vals = [24, 17, 53, 21, 35]
labels = ['Ford', 'Toyota', 'BMV', 'AUDI', 'Jaguar']
fig, ax = plt.subplots()
ax.pie(vals,labels=labels,wedgeprops=dict(width=0.5))