Параллелограмм. Свойства параллелограмма. Трапеция

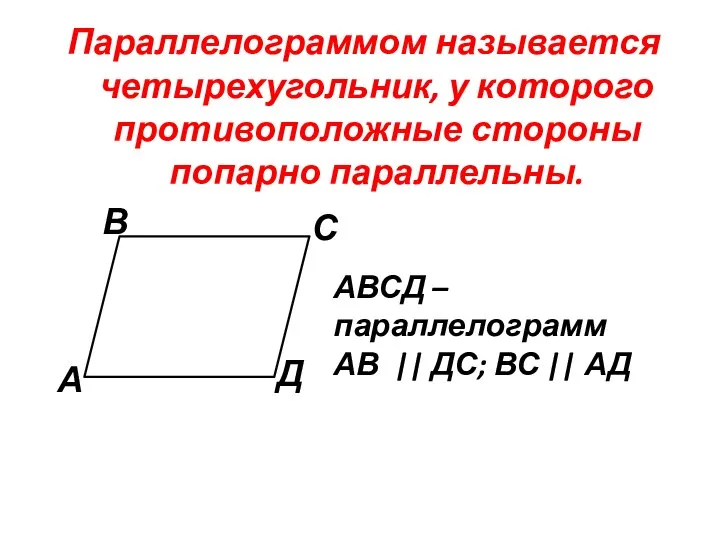
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
А
В
С
Д
АВСД – параллелограмм
АВ || ДС; ВС || АД

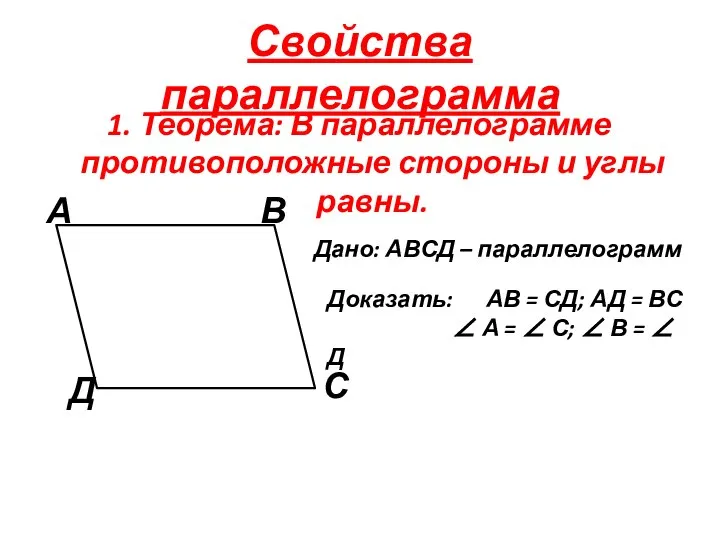
Свойства параллелограмма
1. Теорема: В параллелограмме противоположные стороны и углы равны.
Дано: АВСД – параллелограмм
Доказать: АВ = СД; АД = ВС
∠ А = ∠ С; ∠ В = ∠ Д

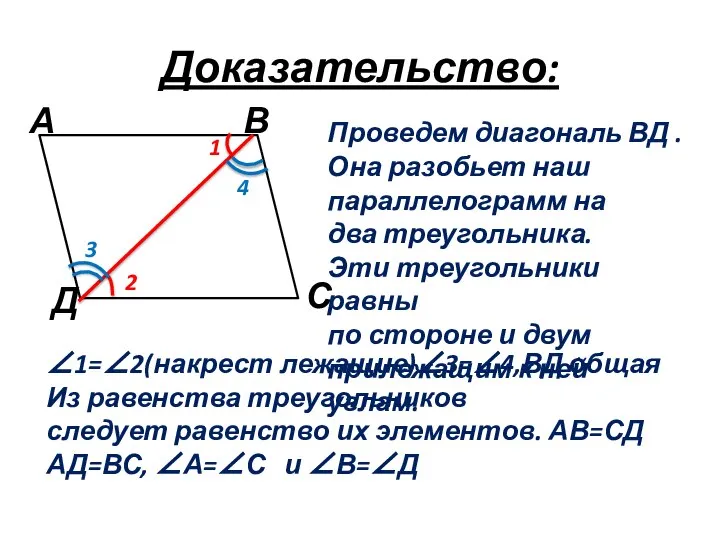
Доказательство:
1
2
3
4
Проведем диагональ ВД .
Она разобьет наш
параллелограмм на
два треугольника.
Эти треугольники равны
по стороне и двум прилежащим к ней углам.
∠1=∠2(накрест лежащие)∠3=∠4,ВД общая
Из равенства треугольников
следует равенство их элементов. АВ=СД
АД=ВС, ∠А=∠С и ∠В=∠Д

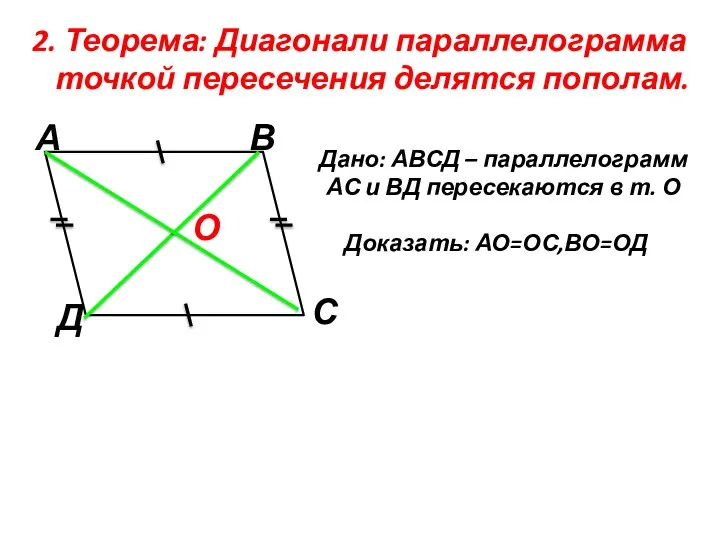
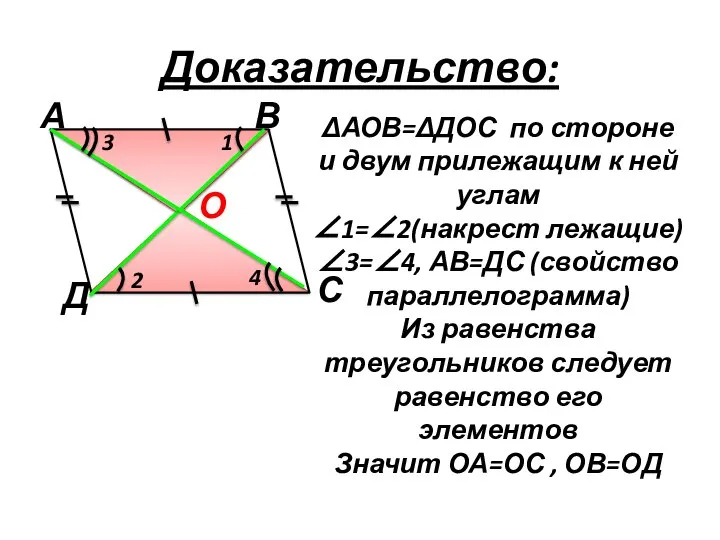
2. Теорема: Диагонали параллелограмма точкой пересечения делятся пополам.
Дано: АВСД – параллелограмм АС и ВД пересекаются в т. О
Доказать: АО=ОС,ВО=ОД
О

ΔАОВ=ΔДОС по стороне и двум прилежащим к ней углам
∠1=∠2(накрест лежащие)
∠3=∠4, АВ=ДС (свойство параллелограмма)
Из равенства треугольников следует равенство его элементов
Значит ОА=ОС , ОВ=ОД
О
2
1
3
4
Доказательство:

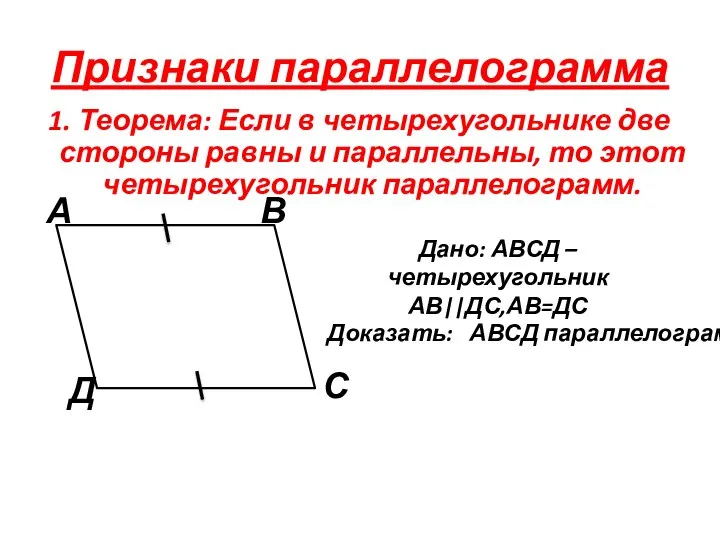
Признаки параллелограмма
1. Теорема: Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.
Дано: АВСД – четырехугольник
АВ||ДС,АВ=ДС
Доказать: АВСД параллелограмм

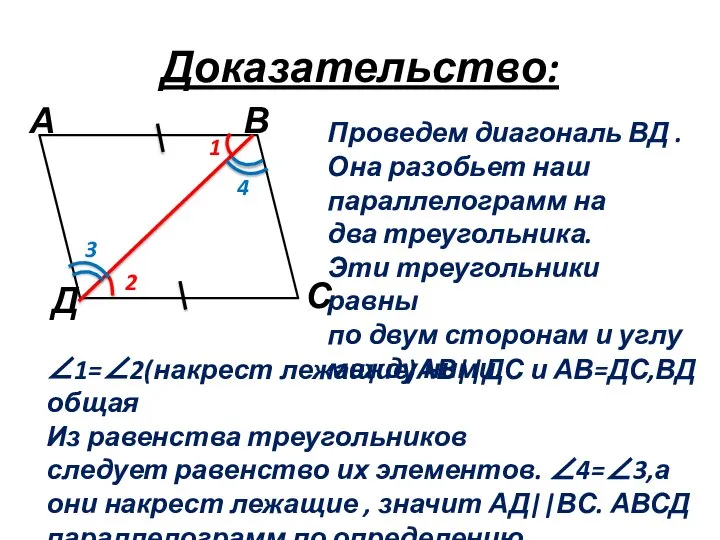
Доказательство:
1
2
3
4
Проведем диагональ ВД .
Она разобьет наш
параллелограмм на
два треугольника.
Эти треугольники равны
по двум сторонам и углу
между ними.
∠1=∠2(накрест лежащие)АВ||ДС и АВ=ДС,ВД общая
Из равенства треугольников
следует равенство их элементов. ∠4=∠3,а они накрест лежащие , значит АД||ВС. АВСД параллелограмм по определению

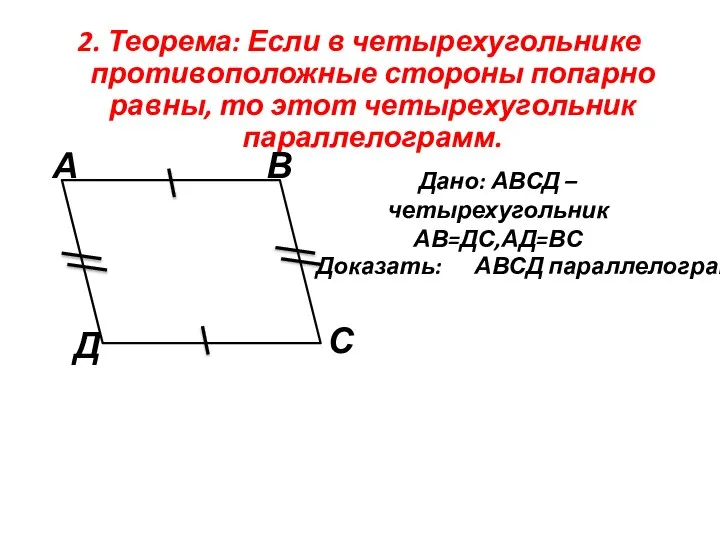
2. Теорема: Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм.
Дано: АВСД – четырехугольник
АВ=ДС,АД=ВС
Доказать: АВСД параллелограмм

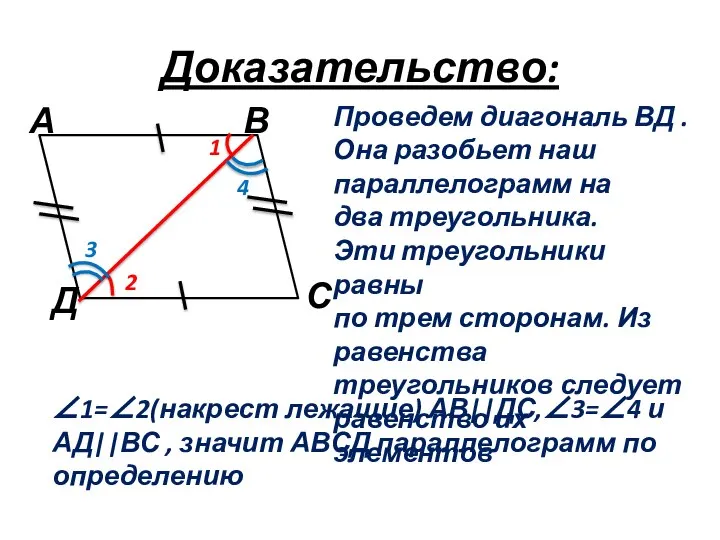
Доказательство:
1
2
3
4
Проведем диагональ ВД .
Она разобьет наш
параллелограмм на
два треугольника.
Эти треугольники равны
по трем сторонам. Из равенства треугольников следует равенство их элементов
∠1=∠2(накрест лежащие) АВ||ДС,∠3=∠4 и АД||ВС , значит АВСД параллелограмм по определению

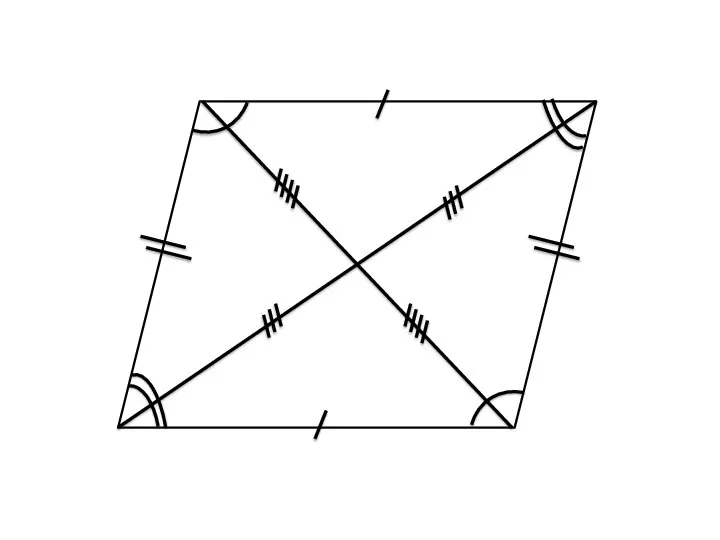
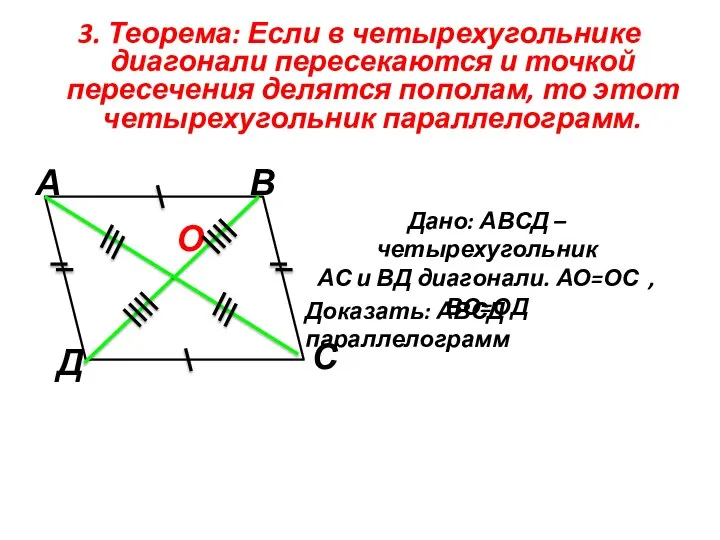
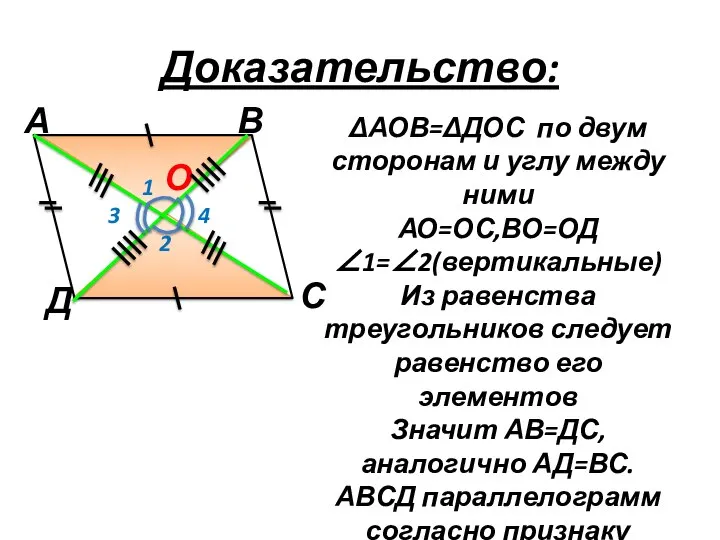
3. Теорема: Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.
Дано: АВСД – четырехугольник
АС и ВД диагонали. АО=ОС , ВО=ОД
Доказать: АВСД - параллелограмм
О

ΔАОВ=ΔДОС по двум сторонам и углу между ними
АО=ОС,ВО=ОД
∠1=∠2(вертикальные)
Из равенства треугольников следует равенство его элементов
Значит АВ=ДС, аналогично АД=ВС.
АВСД параллелограмм согласно признаку
Доказательство:
О
2
1
3
4

Трапеция

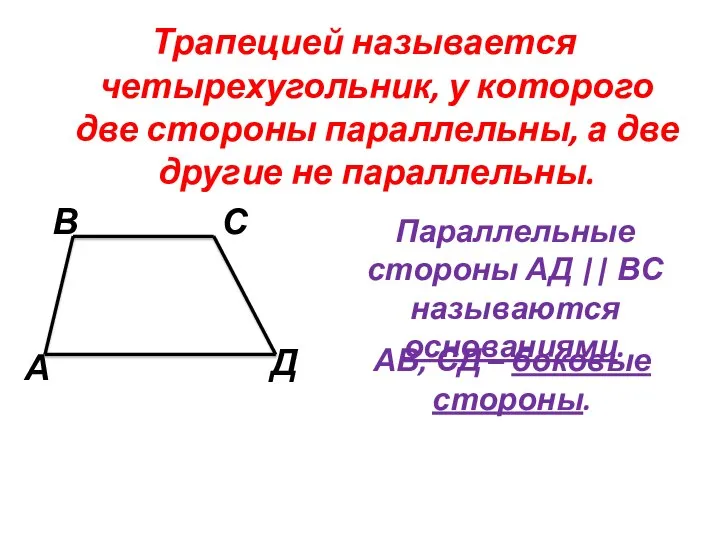
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны АД || ВС называются основаниями.
АВ, СД – боковые стороны.

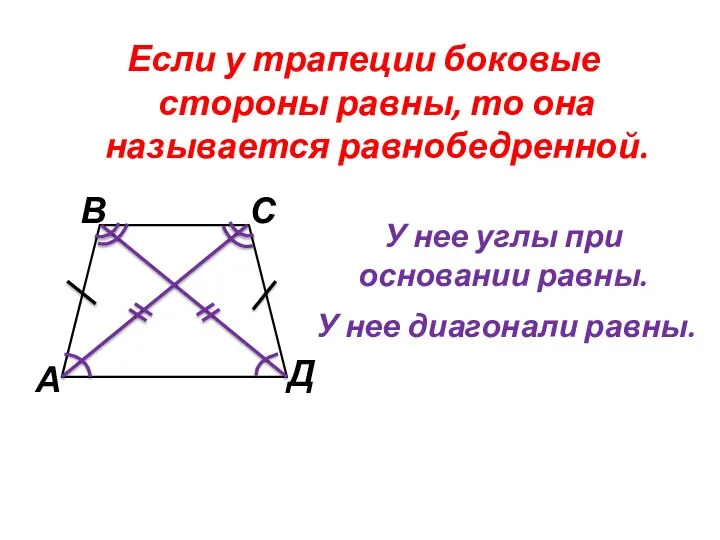
Если у трапеции боковые стороны равны, то она называется равнобедренной.
У нее углы при основании равны.
У нее диагонали равны.
А
В
С
Д