Содержание
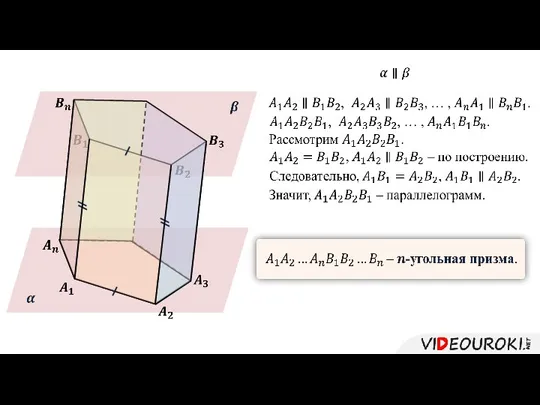
- 3. Параллелограммы – боковыми гранями призмы. А стороны боковых граней, не являющиеся сторонами оснований призмы, называются боковыми
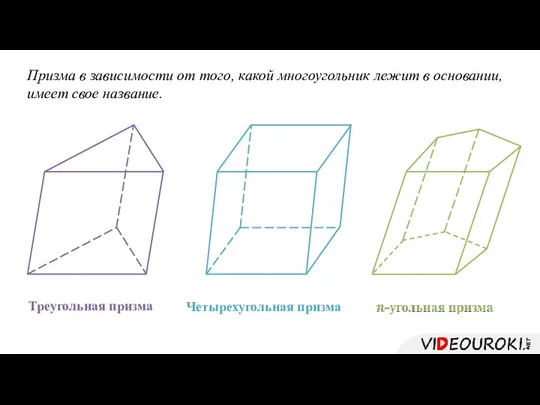
- 4. Призма в зависимости от того, какой многоугольник лежит в основании, имеет свое название. Треугольная призма Четырехугольная
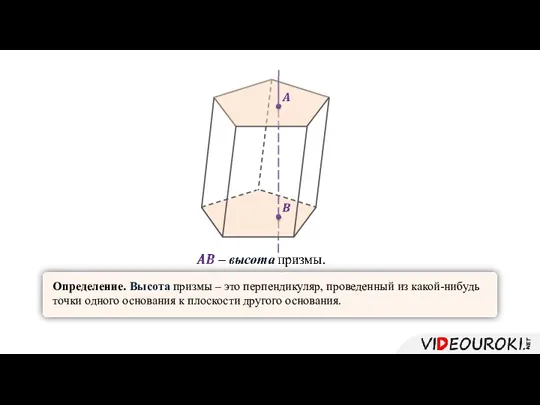
- 5. Определение. Высота призмы – это перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.
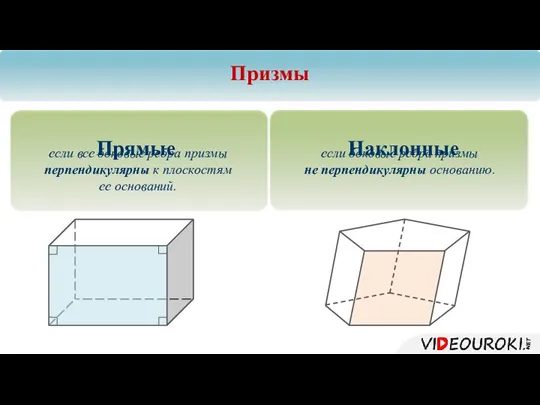
- 6. Призмы Прямые Наклонные если все боковые ребра призмы перпендикулярны к плоскостям ее оснований. если боковые ребра
- 7. Объединение боковых граней называется боковой поверхностью призмы. А объединение всех граней называется полной поверхностью призмы.
- 8. Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. Доказательство.
- 9. Решение.
- 10. Решение.
- 11. Задача. Доказать, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
- 12. Решение.
- 13. Решение.
- 15. Скачать презентацию








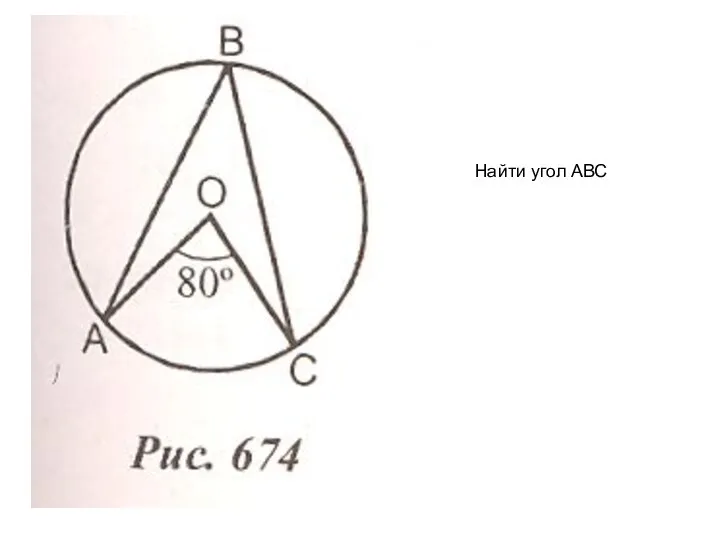 Найти угол АВС
Найти угол АВС Решение задач. Периметр и площадь
Решение задач. Периметр и площадь Применение производной. Задание 8 (профильный уровень)
Применение производной. Задание 8 (профильный уровень) Урок математики
Урок математики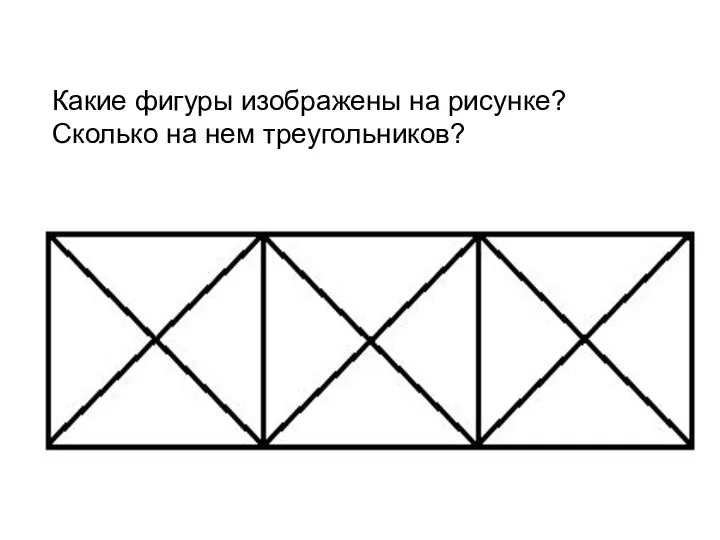 Периметр треугольника
Периметр треугольника Иерархическая кластеризация
Иерархическая кластеризация Проценты чисел
Проценты чисел Подмножество. Операции над множествами. Самостоятельная работа
Подмножество. Операции над множествами. Самостоятельная работа Пропорция
Пропорция Násobíme a delíme s Mimoňmi
Násobíme a delíme s Mimoňmi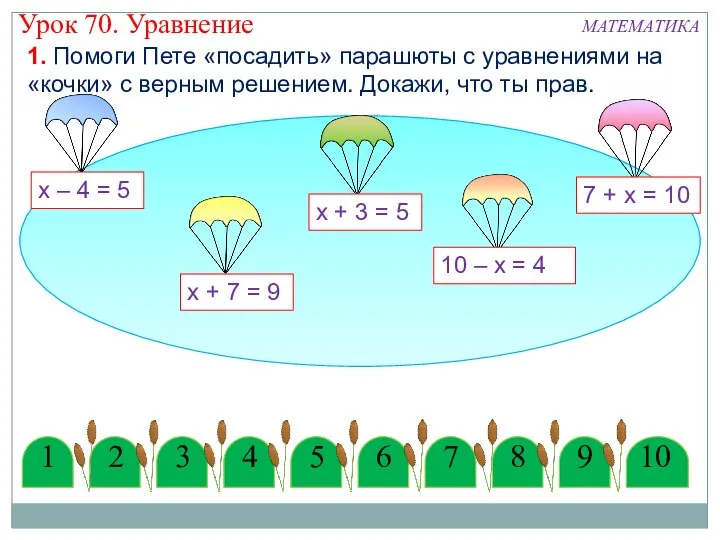 Уравнение. Математика. Урок 70
Уравнение. Математика. Урок 70 Первообразная и интеграл
Первообразная и интеграл Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки Преобразование формул
Преобразование формул Дополнительные задачи. 7 класс
Дополнительные задачи. 7 класс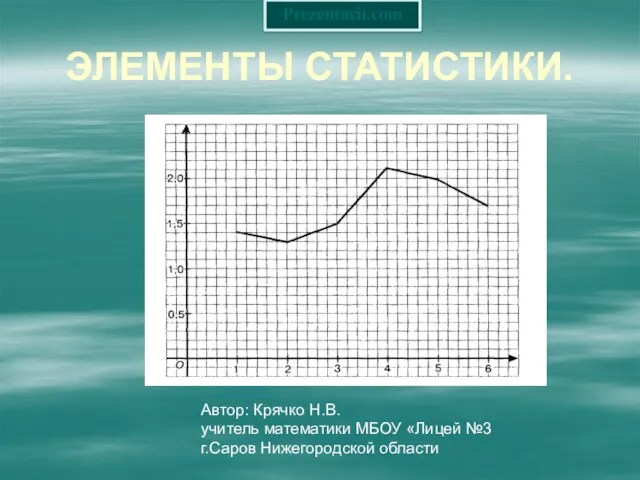 Презентация на тему Элементы статистики
Презентация на тему Элементы статистики  Шкала. Координатный луч
Шкала. Координатный луч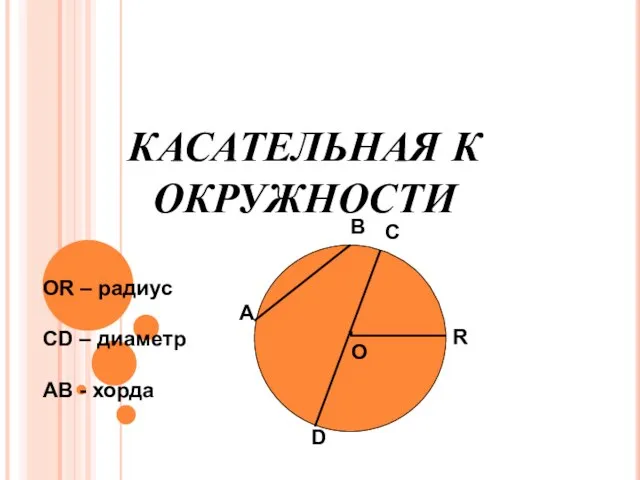 08.09
08.09 Производная вокруг нас
Производная вокруг нас Длина ломанной
Длина ломанной Введение в теорию графов
Введение в теорию графов Геометрические фигуры
Геометрические фигуры Проценты. Ж.Ж. Руссо (1712–1778 гг.)
Проценты. Ж.Ж. Руссо (1712–1778 гг.) Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Разложение многочлена на множители с помощью формулы сокращенного умножения
Разложение многочлена на множители с помощью формулы сокращенного умножения Один - много. 1 класс
Один - много. 1 класс Статистика и ее роль в развитии общества
Статистика и ее роль в развитии общества Правильные многоугольники
Правильные многоугольники