оценки совместного распределения и для вычисления интегралов методом Монте-Карло . Этот алгоритм является частным случаем алгоритма Метрополиса-Гастингса.
Семплирование по Гиббсу замечательно тем, что для него не требуется явно выраженное совместное распределение, а нужны лишь условные вероятности для каждой переменной, входящей в распределение. Алгоритм на каждом шаге берет одну случайную величину и выбирает ее значение при условии фиксированных остальных. Можно показать, что последовательность получаемых значений образуют возвратную цепь Маркова, устойчивое распределение которой является как раз искомым совместным распределением.
Применяется семплирование по Гиббсу в тех случаях, когда совместное распределение случайных величин очень велико или неизвестно явно, но условные вероятности известны и имеют простую форму.
Семплирование по Гиббсу

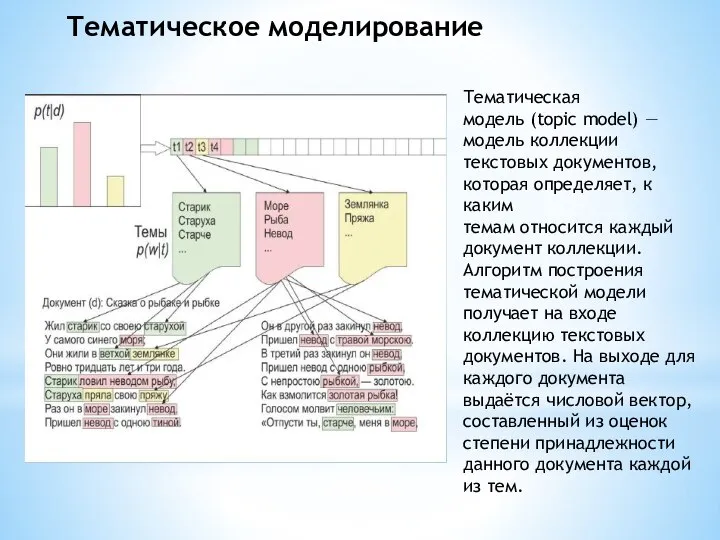





 Множества и операции над ними
Множества и операции над ними Решение и составление ребусов
Решение и составление ребусов Графическое и табличное представление информации
Графическое и табличное представление информации Взаимное расположение прямых и плоскостей
Взаимное расположение прямых и плоскостей Математика в профессии моих родителей
Математика в профессии моих родителей Тела вращения в природе
Тела вращения в природе Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками
Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками Презентация на тему Математика вокруг нас. Узоры и орнаменты на посуде
Презентация на тему Математика вокруг нас. Узоры и орнаменты на посуде  Урок математики в 3 классе
Урок математики в 3 классе Решение тригонометрических уравнений
Решение тригонометрических уравнений Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения
Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения Презентация на тему Параллелепипед (9 класс)
Презентация на тему Параллелепипед (9 класс)  Сложение и вычитание 4
Сложение и вычитание 4 Решение задач с помощью уравнений
Решение задач с помощью уравнений Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Первый признак параллельности прямых
Первый признак параллельности прямых Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը
Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը Сводка и группировка статистических данных
Сводка и группировка статистических данных Теорема Пифагора
Теорема Пифагора Дорогу осилит идущий, а математику мыслящий
Дорогу осилит идущий, а математику мыслящий Векторы на плоскости
Векторы на плоскости Производные тригонометрических функций. 10 класс
Производные тригонометрических функций. 10 класс Вычисление производных. Формулы дифференцирования
Вычисление производных. Формулы дифференцирования Свойство биссектрисы угла
Свойство биссектрисы угла Построение графика функции
Построение графика функции Решение задач
Решение задач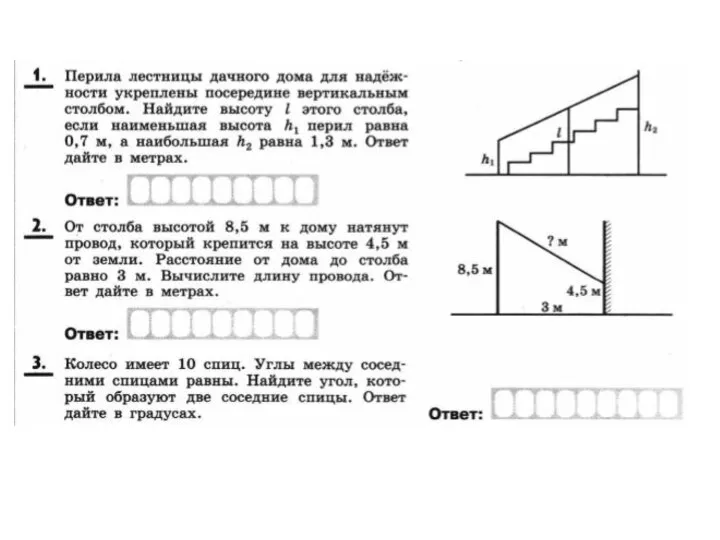 Геометрия, задачи
Геометрия, задачи Действия с многозначными числами
Действия с многозначными числами