Перебор, часть 2

Разбиение числа на слагаемые
Будем считать разбиения, отличающиеся только порядком слагаемых, одинаковыми.
Например, 1 + 7 + 9 и 9 + 1 + 7 одно и тоже.
Пример:
Для числа 5 существует 7 разбиений:
5 = 1 + 1 + 1 + 1 + 1
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 4
5 = 5
Будем генерировать разбиения, в которых числа следуют в порядке не возрастания.

Разбиение числа на слагаемые
N – заданное число
sum – текущая сумма
rez – вектор, содержащий результат
last – последняя цифра, добавленная в разбиение
partition (N, pos, sum, last)
ЕСЛИ sum = N
Вывести первые pos значений вектора rez
ДЛЯ i от last до ( N – sum )
rez[i] = i
partition(N, pos + 1, sum + i, i)

Разбиение числа на слагаемые
Задача
Разбиение числа на слагаемые. Выведите все разбиения числа n на натуральные слагаемые. Разбиения, отличающиеся только порядком слагаемых, считаются одинаковыми, поэтому выводите слагаемые в каждом разбиении в порядке не убывания.
Входные данные
Натуральное число n.
Выходные данные
Выведите разбиения числа n на слагаемые в лексикографическом порядке, каждое разбиение - в отдельной строке. Числа в каждом разбиении должны идти в порядке не убывания, разделяться знаками “+” (без пробелов) и в сумме давать n.
Пример входных данных
5
Пример выходных данных
1+1+1+1+1
1+1+1+2
1+1+3
1+2+2
1+4
2+3
5
В качестве ответа на задание выберите разбиение на слагаемые числа n = 7 с номером 10 в лексикографическом порядке. Для примера из условия разбиение с номером 4 имеет вид "1+2+2”.

Задача коммивояжёра

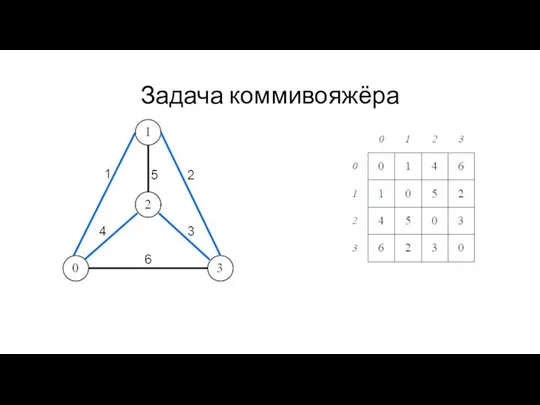
Задача коммивояжёра
N – количество городов
а – матрица путей
city – вектор посещений (начальные значения нулевые)
way - текущий путь (содержит номера городов в порядке посещения)
len – длина текущего пути
cur – номер текущего города
already – количество посещённых городов
findWay(a, city, way, len, cur, already)
ЕСЛИ already = N – 1
если существует путь в начальный город
вывести текущий путь и его длину (len + длина последнего участка)
ДЛЯ i от 0 до N
ЕСЛИ а[i][cur] не равно 0
если city[i] = 0
city[i] = 1
way[already] = i
findWay(a, city, way, len + a[i][cur], I, already + 1)
city[i] = 0

Задача коммивояжёра
key = 0
min = 0
findWay(a, city, way, len, cur, already)
ЕСЛИ already = N – 1
ЕСЛИ существует путь в начальный город
ЕСЛИ key = 0
min = len + длина последнего участка
key = 1
ИНАЧЕ
ЕСЛИ (len + длина последнего участка) < min
min = len + длина последнего участка
ДЛЯ i от 0 до N
ЕСЛИ а[i][cur] не равно 0
ЕСЛИ city[i] = 0
city[i] = 1
way[already] = i
findWay(a, city, way, len + a[i][cur], I, already + 1)
city[i] = 0

Задача коммивояжёра
Для самостоятельного решения
В первой строке задано натуральное число n - количество городов. Следующие n строк содержат длины дорог aij​ , по n чисел в каждой строке. Города пронумерованы числами от 0 до n−1. Гарантируется, что числа aij​ - натуральные, aij​=aji​ и aii​=0 для i и j от 0 до n−1.
Выходные данные
В первой строке выведите одно целое число - минимальную длину пути коммивояжера. Во второй строке выведите последовательность из n чисел - сам путь. Путь должен содержать номера городов в порядке обхода и начинаться с номера 0.

Домашнее задание
Перебор правильных скобочных последовательностей с двумя типами скобок. Выведите все правильные скобочные последовательности с двумя типами скобок ‘(’, ‘)’, ‘[‘, ‘]’, содержащие 2n скобок, в лексикографическом порядке. В последовательности могут встречаться оба типа скобок или только один из них.
Входные данные
Натуральное число n.
Выходные данные
Выведите все правильные скобочные последовательности в лексикографическом порядке, каждую последовательность - в отдельной строке, без пробелов. Считайте, что ‘(’ < ‘)’ < ‘[‘ < ‘]’.
Тестовое задание
Найдите последовательность для n = 7 (состоящую из 14 скобок) с номером 8233 в лексикографическом порядке.