6a639551ce27612e

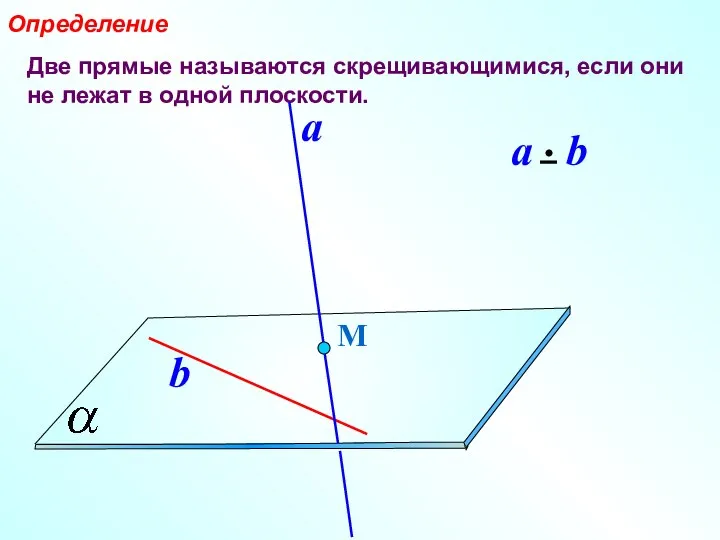
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Определение
М
a
b

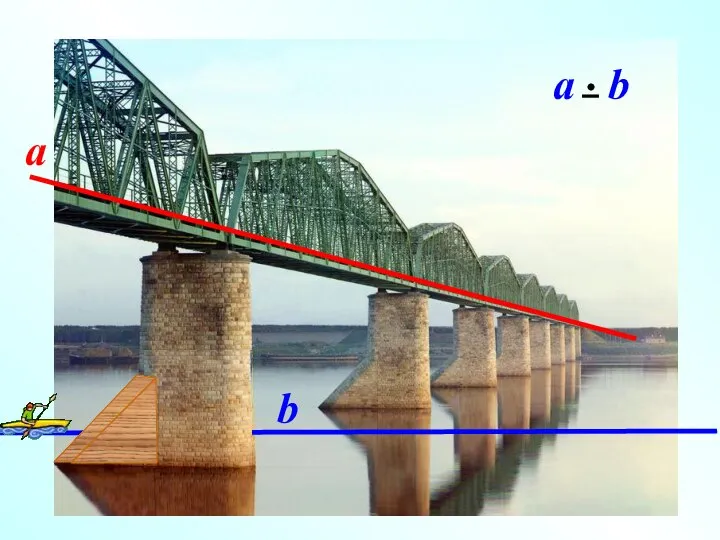
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.

a
b

Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.

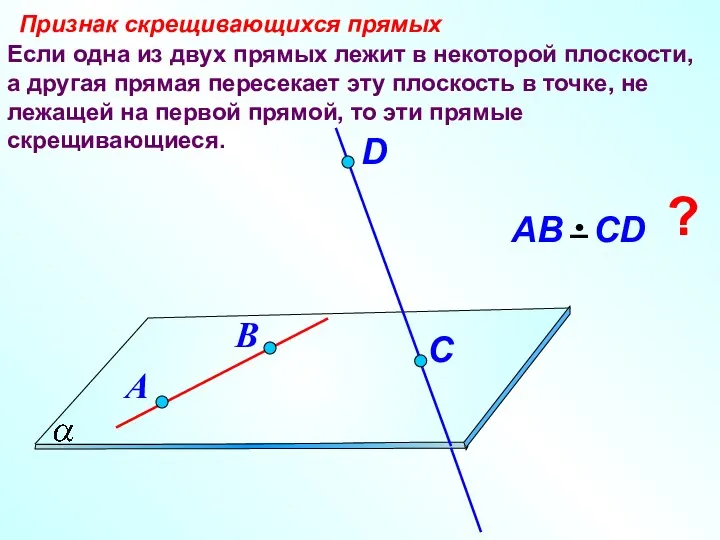
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Признак скрещивающихся прямых
D
В
А
C
?

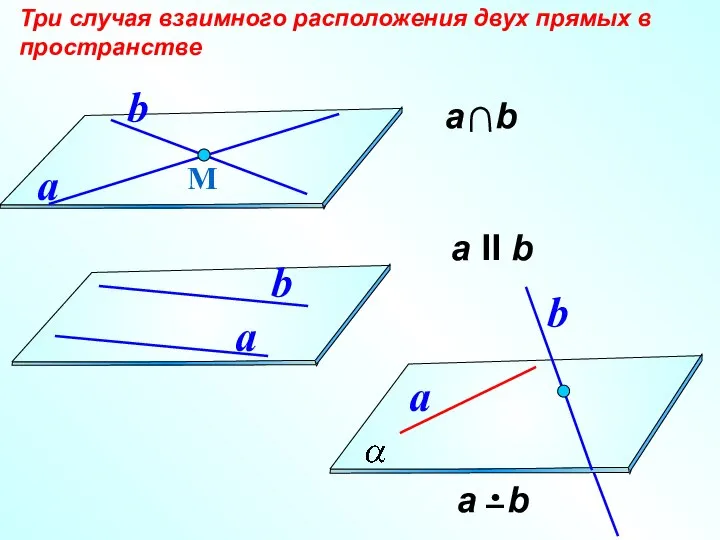
а II b
Три случая взаимного расположения двух прямых в пространстве
М
a
b
a
b
a
b

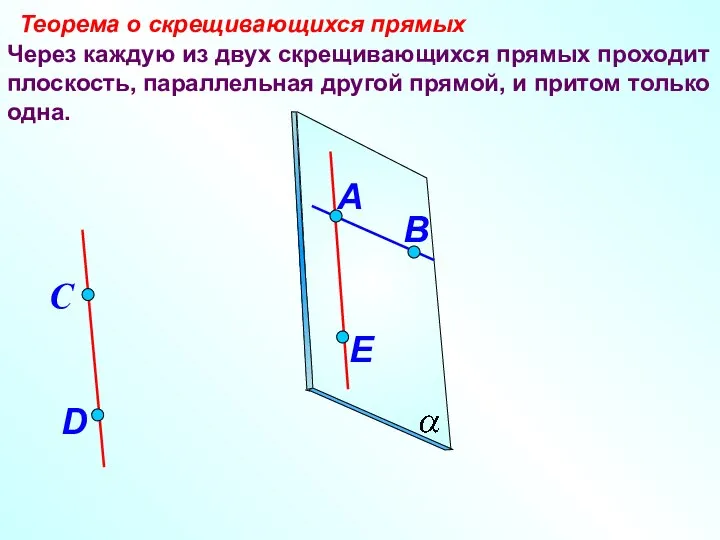
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Теорема о скрещивающихся прямых
D
С
B
A

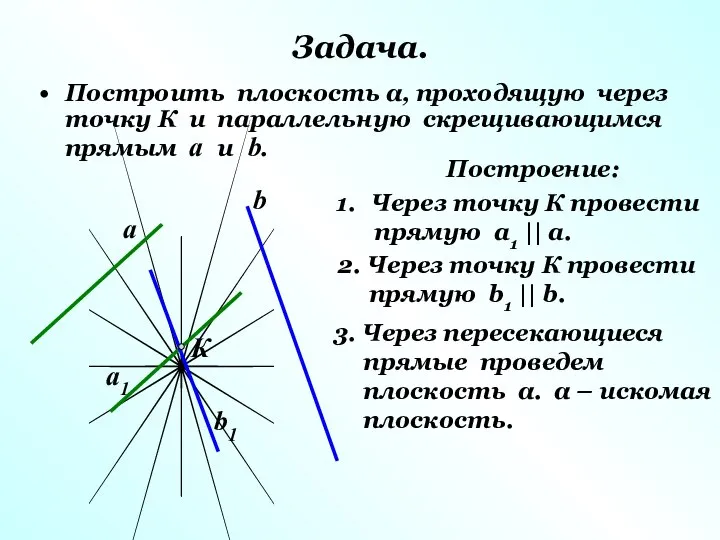
Задача.
Построить плоскость α, проходящую через точку К и параллельную скрещивающимся прямым а и b.
Построение:
Через точку К провести
прямую а1 || а.
2. Через точку К провести
прямую b1 || b.
а
b
К
а1
b1
3. Через пересекающиеся
прямые проведем
плоскость α. α – искомая
плоскость.

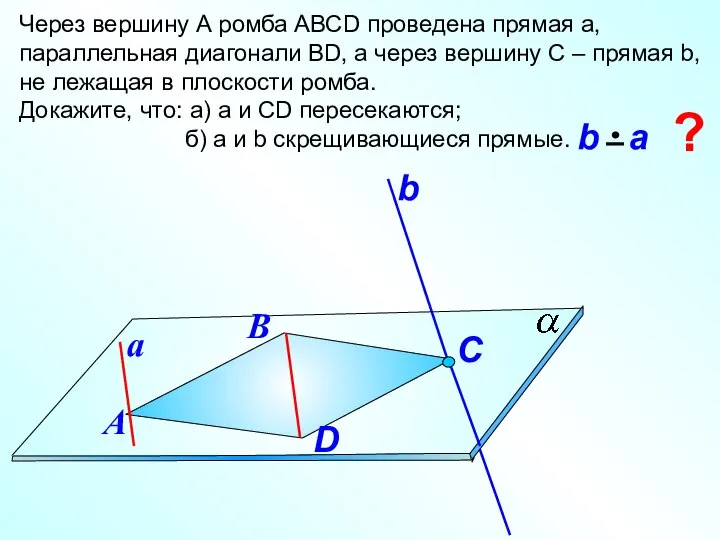
Через вершину А ромба АВСD проведена прямая а, параллельная диагонали ВD, а через вершину С – прямая b, не лежащая в плоскости ромба.
Докажите, что: а) а и СD пересекаются;
б) а и b скрещивающиеся прямые.
В
А
C
?
a
D

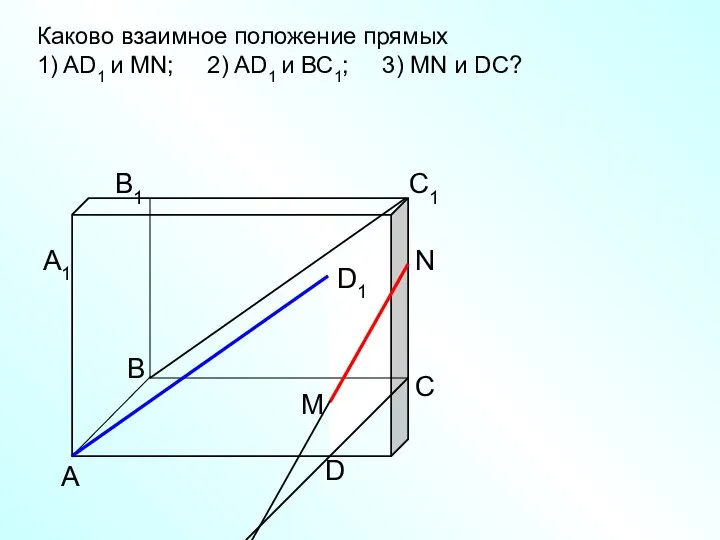
А
D
С
В
B1
С1
D1
А1
Каково взаимное положение прямых
1) AD1 и МN; 2) AD1 и ВС1; 3) МN и DC?
N
M

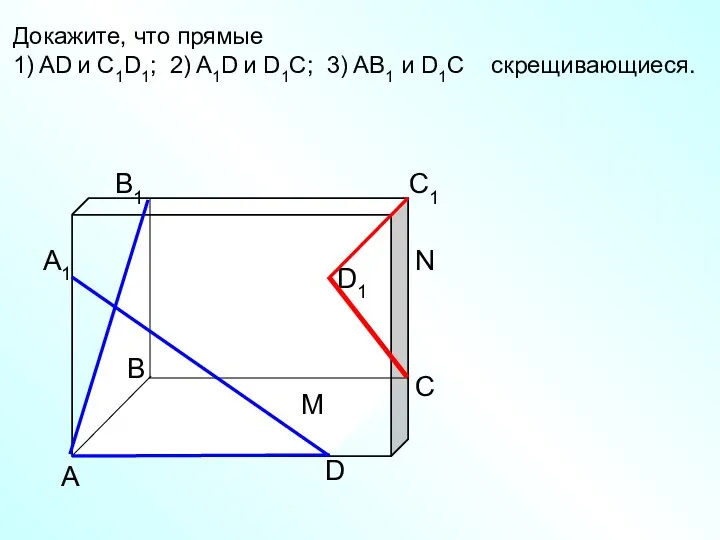
А
D
С
В
B1
С1
D1
А1
Докажите, что прямые
1) AD и C1D1; 2) A1D и D1C; 3) AB1 и D1C скрещивающиеся.
N
M

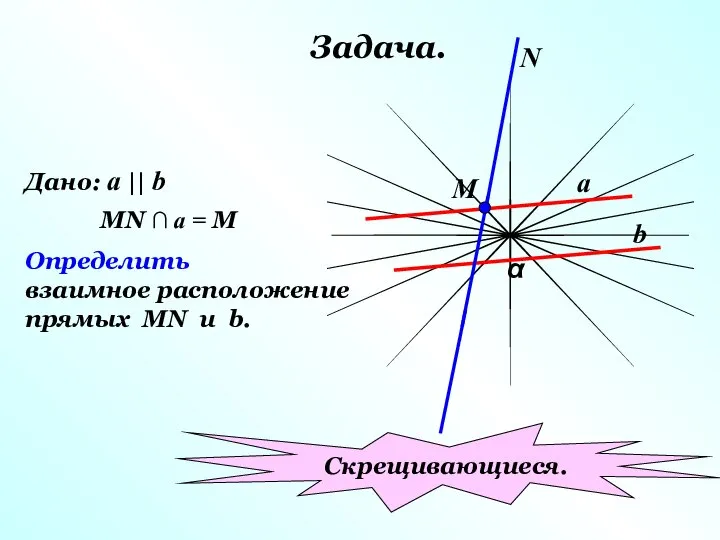
Задача.
α
a
b
М
N
Дано: a || b
MN ∩ a = M
Определить
взаимное расположение
прямых MN u b.
Скрещивающиеся.

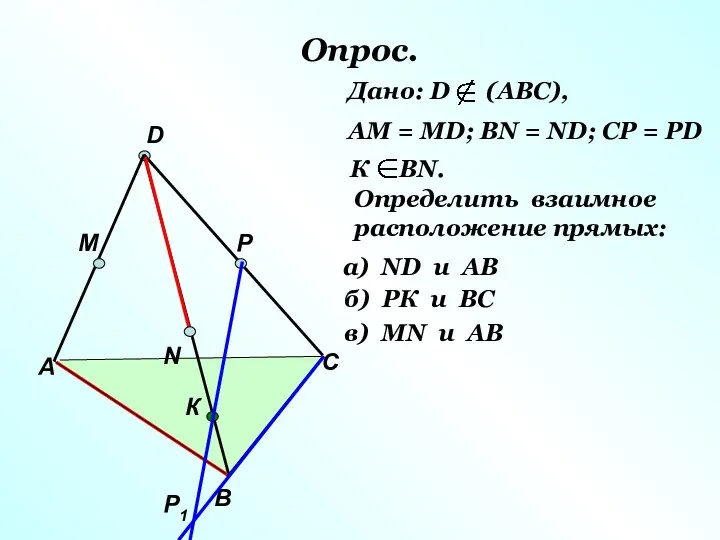
Опрос.
А
В
С
D
M
N
P
Р1
К
Дано: D (АВС),
АМ = МD; ВN = ND; CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB

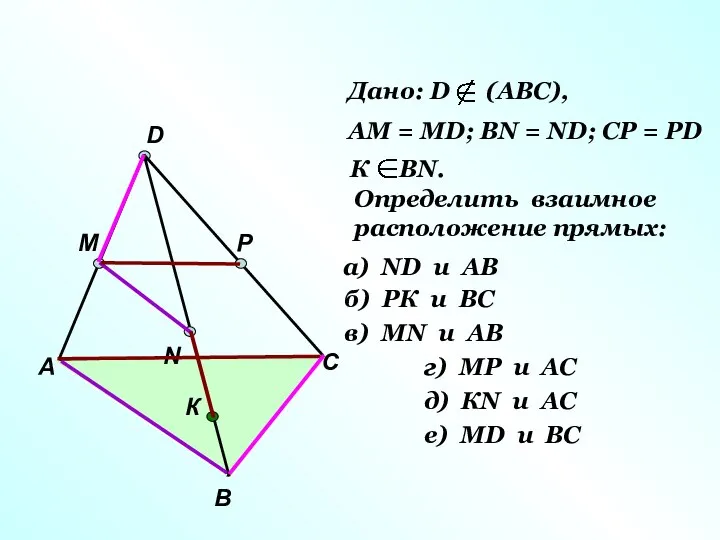
А
В
С
D
M
N
P
К
Дано: D (АВС),
АМ = МD; ВN = ND; CP = PD
К ВN.
Определить взаимное
расположение прямых:
а) ND и AB
б) РК и ВС
в) МN и AB
г) МР и AС
д) КN и AС
е) МD и BС