Содержание
- 2. «Стоя на одном месте новых горизонтов не откроешь.»
- 3. arccos a arcsin a ? arccos a = t ⬄ arccos (-a) arcsin (-a) arcsin a
- 4. Имеет ли смысл выражение? Вычислите:
- 5. Решите уравнение: Ответы: ? корней нет
- 6. Тригонометри- ческие уравнения
- 7. Уравнение cos t = a 0 x y 2. Отметить точку а на оси абсцисс. 3.
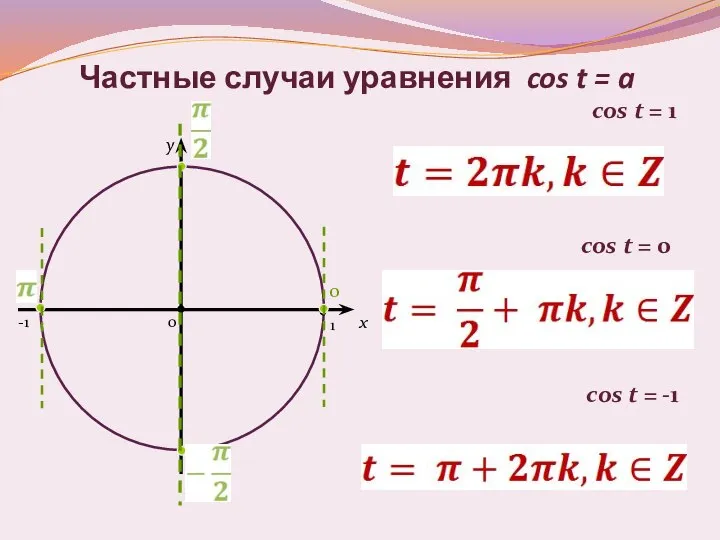
- 8. Частные случаи уравнения cos t = a x y cos t = 0 cos t =
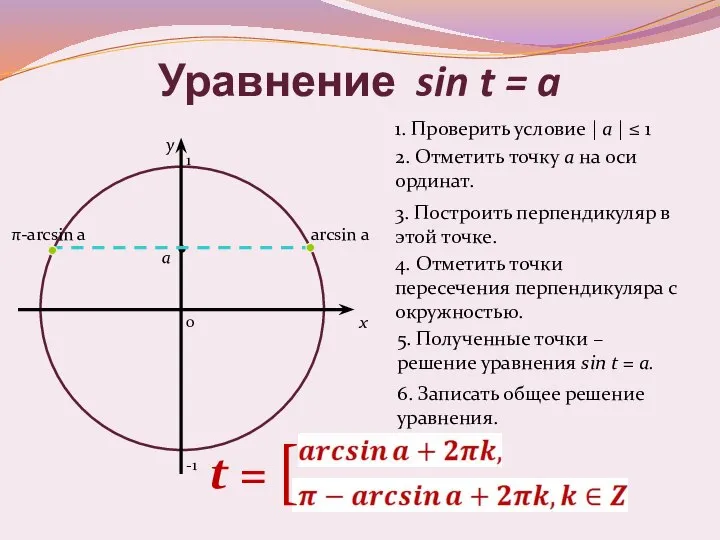
- 9. Уравнение sin t = a 0 x y 2. Отметить точку а на оси ординат. 3.
- 10. [
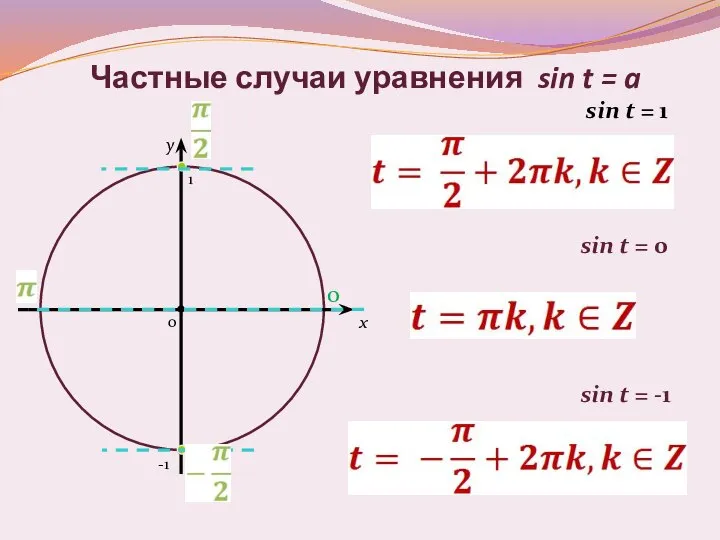
- 11. Частные случаи уравнения sin t = a x y sin t = 0 sin t =
- 12. Решите уравнения: Сравните:
- 13. Решите уравнение:
- 14. Проверь себя! sin t = a, ǀаǀ≤1 cos t = a, ǀаǀ≤1
- 15. ОТВЕТЫ:
- 16. Решите уравнение:
- 17. Домашнее задание: § 22 (п.1-3) № 11(б), 14, 31, 33(в)*, тест: www.uztest.ru [ (?)
- 18. «Уравнение есть равенство, которое ещё не является истинным, но которое стремятся сделать истинным, не будучи уверенным,
- 19. Спасибо за внимание!
- 21. Скачать презентацию















 Подготовка к ГИА. Демоверсия 2013
Подготовка к ГИА. Демоверсия 2013 Мотивация … Статистика
Мотивация … Статистика Парная регрессия и корреляция
Парная регрессия и корреляция Простые и составные числа
Простые и составные числа Единицы измерения времени. Тренажёр
Единицы измерения времени. Тренажёр Дифференциальные уравнения
Дифференциальные уравнения Функция y=k/x, её график и свойства. 8 класс. Урок 2
Функция y=k/x, её график и свойства. 8 класс. Урок 2 Духовно-нравственное воспитание на уроках математики
Духовно-нравственное воспитание на уроках математики Особенности применения средств измерений в качестве эталонов единицы величины
Особенности применения средств измерений в качестве эталонов единицы величины Показательная функция
Показательная функция Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Площадь треугольника
Площадь треугольника Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Коррекция СУ
Коррекция СУ Римские цифры. 3 класс
Римские цифры. 3 класс Нулевая гипотеза
Нулевая гипотеза Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Презентация на тему Математический диктант (4 класс)
Презентация на тему Математический диктант (4 класс)  Свойства четырёхугольников
Свойства четырёхугольников idkwhythatair
idkwhythatair Виды многоугольников
Виды многоугольников Числа от 1 до 5. Состав числа 5
Числа от 1 до 5. Состав числа 5 Письмо цифры 6
Письмо цифры 6 Сложение смешанных дробей
Сложение смешанных дробей Среднее арифметическое
Среднее арифметическое Стереометрия. Подготовка к ЕГЭ, задание В11
Стереометрия. Подготовка к ЕГЭ, задание В11 Математические методы в экономике. Лекция 8
Математические методы в экономике. Лекция 8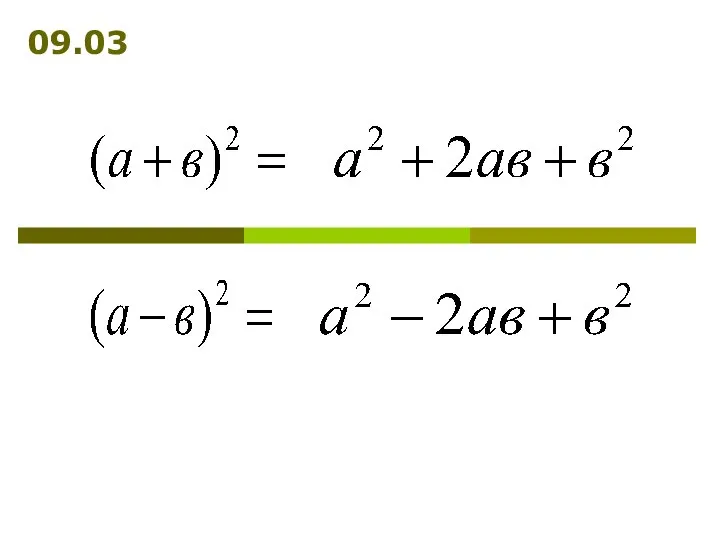 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения