Слайд 2Классическое определение вероятности.

Слайд 3Правило сложения.
Если некоторый объект A можно выбрать k способами, а объект B - l способами (не

такими как А), то объект "или А или В" можно выбрать m + l способами.
Слайд 4Правило умножения.
Если объект А можно выбрать k способами, а после каждого такого выбора другой

объект В можно выбрать (независимо от объекта А) l способами, то пары объектов А и B можно выбрать m·l способами.
Слайд 5Задача № 1.
В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите

вероятность того, что один случайно выбранный для контроля насос не подтекает.
Слайд 6
Решение:
Событие A - "выбранный насос не подтекает".
Всего насосов n = 1000. Из

них 5 подтекают, значит не подтекают
m = 1000 - 5 = 995.
По формуле P =n/m= 995/1000 =0,995
Слайд 7Задача № 2
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и

перестали ходить. Найдите вероятность того, что часовая стрелка застыла, пройдя отметку 11 часов, но не дойдя до отметки 2 часа.
Слайд 8Решение:
P=n/m
m=12 (12 часовой циферблат)
n=3 ( стрелка не прошла 3 часа)
P=3/12=0,25

Слайд 9Задача № 3 .
Научная конференция проводится в 4 дня. Всего запланировано 50

докладов: первые два дня по 15 докладов, остальные распределены поровну между третьим и четвёртым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Слайд 10
Решение:
Получается, что в первый день 15 докладов, во второй 15 докладов, в

третий 10 и в четвертый тоже 10 докладов. Всего докладов 50 (m=50).
Профессор М. мог попасть в любой из этих 50 докладов равновероятно.
В последний день запланировано 10 докладов (n=10), т.е. вероятность, что профессор М. будет выступать в последний день равна:
P=10/50 = 0,2.
Слайд 11
Задача № 4.
Даша дважды бросает игральный кубик. В сумме у нее выпало

8 очков. Найдите вероятность того, что при одном из бросков выпало 2 очка.
Слайд 12
Решение:
Чтобы выпало 8 очков за 2 броска, нужно чтобы при каждом бросании

кубика было больше 1.
Получается, что 8 очков может выпасть так:
2 и 6, 3 и 5, 4 и 4, 5 и 3, 6 и 2.
m=5 (все исходы), а n=2.
Вероятность того, что при одном из бросков выпало 2 очка, равна
P= 2/5=0,4.
Слайд 13Задача № 5.
Игральную кость (кубик) бросили один раз. Какова вероятность того, что

выпало менее 4 очков?
Слайд 14
Решение:
У кубика 6 граней, поэтому всего возможно 6 вариантов: 1, 2, 3,

4, 5 и 6 очков. Получаем, что m = 6 — по числу граней.
Нас интересуют случаи, когда выпадает менее 4 очков. Другими словами, если выпадет 1, 2 или 3 очка, нас это устраивает. Всего таких вариантов n = 3. Находим вероятность:
P = n/m = 3/6 = 1/2 = 0,5.
Слайд 15Задача № 6.
Игральную кость (кубик) бросили один раз. Какова вероятность того, что

выпало не менее 4 очков?
Слайд 16
Решение:
Фраза «не менее 4 очков» означает, что нас интересует 4, 5 и

6 очков. Поэтому n = 3.
Всего возможно 6 вариантов (по числу граней кубика), поэтому
m = 6.
Осталось найти вероятность:
P = n/m = 3/6 = 1/2 = 0,5
Слайд 17Задача № 7.
Игральную кость (кубик) бросили один раз. Какова вероятность того, что

выпало нечетное число очков?
Слайд 18
Решение:
Возможные варианты: 1, 2, 3, 4, 5 и 6 очков. Поэтому m

= 6.
Из указанных чисел являются нечетными лишь 1, 3 и 5 — всего 3 числа (откуда заключаем, что n = 3). Осталось найти вероятность:
P = n/m = 3/6 = 1/2 =0,5.
Слайд 19Задача № 8.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того,

что в сумме выпадет 8 очков. Результат округлите до сотых.
Слайд 20
Решение:
Бросаем первую кость — шесть исходов. И для каждого из них возможны

еще шесть — когда мы бросаем вторую кость.
Получаем, что у данного действия — бросания двух игральных костей — всего 36 возможных исходов, так как 6² = 36.
А теперь — благоприятные исходы:
2 и 6;3 и 5; 4 и 4 ;5 и 3 ;6 и 2
Вероятность выпадения восьми очков равна P = n/m = 5/36 ≈ 0,14.
Слайд 21Задача № 9.
Стрелок попадает в цель с вероятностью 0,9. Найдите вероятность того,

что он попадёт в цель четыре раза выстрела подряд.
Слайд 22
Решение:
Если вероятность попадания равна 0,9 — следовательно, вероятность промаха 0,1.
Вероятность двух

попаданий подряд равна 0,9 • 0,9 = 0,81.
А вероятность четырех попаданий подряд равна
0,9 •0,9 •0,9• 0,9 = 0,6561.
Слайд 23Задача № 10.
Ковбой Джон попадает в муху на стене с вероятностью 0,9,

если
стреляет из пристрелянного револьвера. Если Джон стреляет из
непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На
столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон
видит на стене муху, наудачу хватает первый попавшийся револьвер и
стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Слайд 24
Решение:
Вероятность того, что Джон возьмет пристрелянный револьвер равна 3/10,а непристярелянный- 7/10.
Вероятность

попадания из пристрелянного револьвера равна 0,3•0,9,а из непристрелянного- 0,7•01.
Джон убьет муху с вероятностью 0,27+0,07=0,34.
Промахнется он с вероятностью
1-0,34=0,66.
Слайд 25Задача № 11.
По отзывам покупателей Василий Васильевич оценил надёжность двух интернет‐магазинов. Вероятность

того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,88. Василий Васильевич заказал товар сразу в обоих магазинах. Считая, что интернет‐магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Слайд 26
Решение:
Вероятность недоставки из магазина А равна 1-0,8=0,2, а из магазина В-
1-0,88=0,12.

Вероятность того, что ни один магазин не доставит товар 0,2•0,12=0,024.

























 Логика и доказательство
Логика и доказательство Математика и здоровье. Математика и медицина
Математика и здоровье. Математика и медицина Математика. Раздел 6. Метод координат в пространстве. Занятие 65. Простейшие задачи в координатах
Математика. Раздел 6. Метод координат в пространстве. Занятие 65. Простейшие задачи в координатах Взаимное расположение прямой и окружности, двух окружностей
Взаимное расположение прямой и окружности, двух окружностей ВПР вариант 16 № 11. Решение трудной задачи
ВПР вариант 16 № 11. Решение трудной задачи Волшебная страна - Геометрия. Занятие 3
Волшебная страна - Геометрия. Занятие 3 Степень с натуральным показателем. Определение степени. 7 класс
Степень с натуральным показателем. Определение степени. 7 класс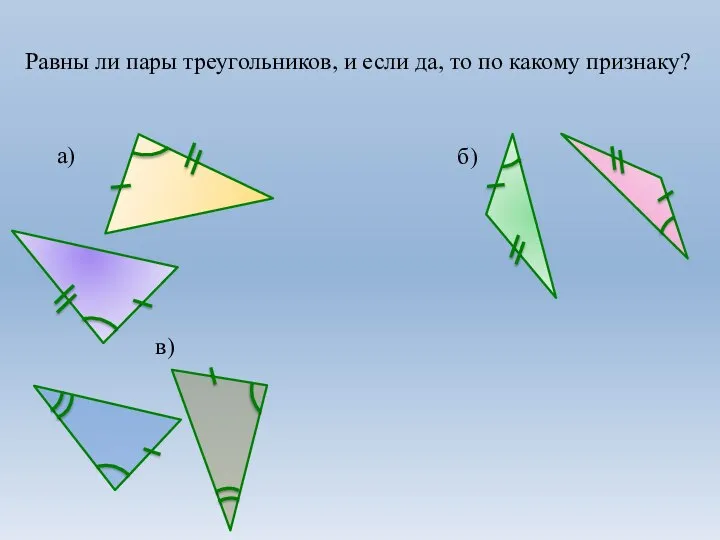 Второй признак равенства треугольников. 7 класс
Второй признак равенства треугольников. 7 класс Показательные неравенства
Показательные неравенства Треугольники. Решение задач
Треугольники. Решение задач Угол и биссектриса
Угол и биссектриса Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Решение неравенств с одной переменной
Решение неравенств с одной переменной Лабиринты. Решение найденных лабиринтов и поиск универсальных правил
Лабиринты. Решение найденных лабиринтов и поиск универсальных правил Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Неравенства и системы неравенств
Неравенства и системы неравенств Нумерация чисел от 21 до 100. Тренажёр-раскраска
Нумерация чисел от 21 до 100. Тренажёр-раскраска Деление с остатком
Деление с остатком Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Многогранники и тела с кривыми поверхностями
Многогранники и тела с кривыми поверхностями Множества и операции над ними
Множества и операции над ними Тестирование
Тестирование Фигуры вращения
Фигуры вращения Пропорция. Основное свойство пропорции
Пропорция. Основное свойство пропорции Таблица единиц площади
Таблица единиц площади Матрица размера m x n
Матрица размера m x n Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Электронные таблицы. Построение графиков и диаграмм
Электронные таблицы. Построение графиков и диаграмм