Содержание
- 2. Саша, над чем это ты задумался? Я разгадываю загадки. И осталaсь последняя, которую разгадать не получается.
- 3. Так это же уравнение. Равенство, содержащее букву, значение которой нужно найти. Точно! И мы умеем их
- 4. Давай. А давай мы поговорим с Мудряшом о решении уравнений. Может, он расскажет нам что-то новое.
- 5. Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания.
- 6. Устный счёт Сверимся?
- 7. Ребята, вы уже вспомнили, что уравнением называют равенство, содержащее букву, значение которой надо найти. И мы
- 9. А теперь посмотрите на следующее уравнение. Для его решения мы не сможем применить ни одно из
- 10. Очевидно, что если к двум равным числам прибавить одно и то же число, то снова получим
- 11. Запомните! Если к обеим частям уравнения прибавить (или из обеих частей вычесть) одно и то же
- 12. Причём, если уравнение не имеет корней, то прибавляя к обеим частям уравнения одно и то же
- 13. Правильно.
- 14. Запомните! Если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак
- 16. Получается, что мы умножили обе части уравнения на одно и то же число и получили уравнение,
- 17. Запомните! Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля
- 18. А почему мы не можем умножать на нуль обе части уравнения? Ребята, а сейчас давайте выполним
- 19. Решите уравнение: Задание № 1 Решение:
- 20. Решите уравнение: Задание № 2 Решение:
- 21. Итоги урока Если к обеим частям уравнения прибавить (или из обеих частей вычесть) одно и то
- 23. Скачать презентацию



















 Построение графиков в MathCAD
Построение графиков в MathCAD Квадратичная функция. Решение текстовых задач
Квадратичная функция. Решение текстовых задач Многогранники: выпуклые призмы и антипризмы
Многогранники: выпуклые призмы и антипризмы Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Вычисление определенных интегралов
Вычисление определенных интегралов Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Множество и его элементы
Множество и его элементы Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Площадь фигур. Свойства площадей
Площадь фигур. Свойства площадей Математический турнир Умники и умницы
Математический турнир Умники и умницы Презентация на тему Рещение линейных уравнений
Презентация на тему Рещение линейных уравнений  Игра - путешествие В стране занимательной математики
Игра - путешествие В стране занимательной математики Математическая грамотность. Урок 1
Математическая грамотность. Урок 1 Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями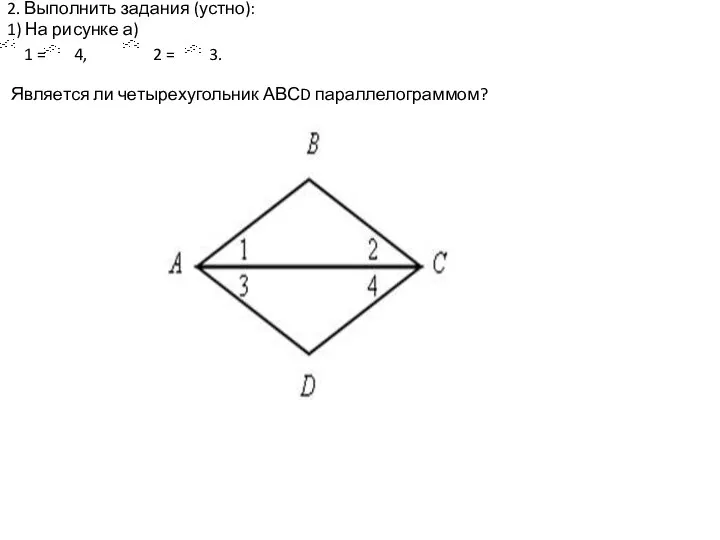 Параллелограмм и трапеция. Урок 4
Параллелограмм и трапеция. Урок 4 Теорема Пифагора
Теорема Пифагора Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -  Вычисление производных. Формулы дифференцирования
Вычисление производных. Формулы дифференцирования Упрощение логических выражений
Упрощение логических выражений Системы неравенств с двумя переменными
Системы неравенств с двумя переменными Поиск сокровищ. Изучений геометрических фигур
Поиск сокровищ. Изучений геометрических фигур Деление суммы на число
Деление суммы на число Презентация на тему Умножение двузначного числа на однозначное (3 класс)
Презентация на тему Умножение двузначного числа на однозначное (3 класс)  Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра-тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Презентация на тему Перебор возможных вариантов
Презентация на тему Перебор возможных вариантов  Степень с отрицательным показателем
Степень с отрицательным показателем