Взаимное расположение прямой и окружност

Проговорите ответы на вопросы:
Какие прямые называются параллельными?
Какие прямые называются перпендикулярными?
Что называют расстоянием от точки до прямой?
Каким может быть взаимное расположение прямой и окружности?
Как называется прямая, имеющая с окружностью две общие точки?
Как называется прямая, имеющая с окружностью одну общую точку?

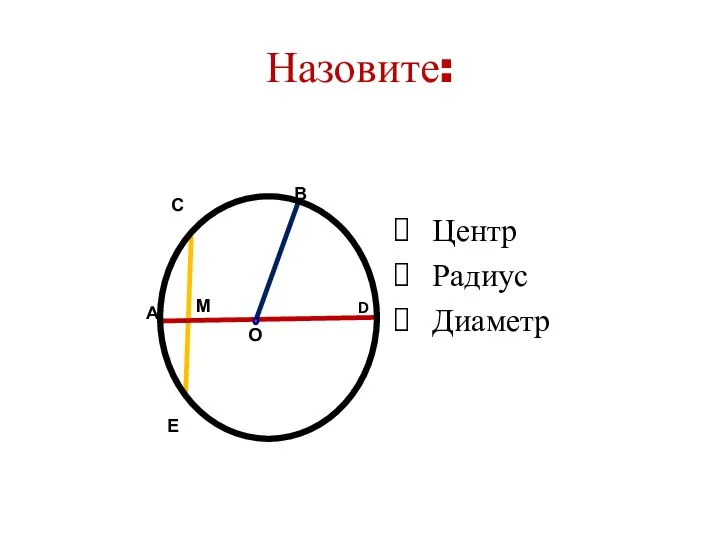
Назовите:
Центр
Радиус
Диаметр
Е
О
В
D
М
А
С

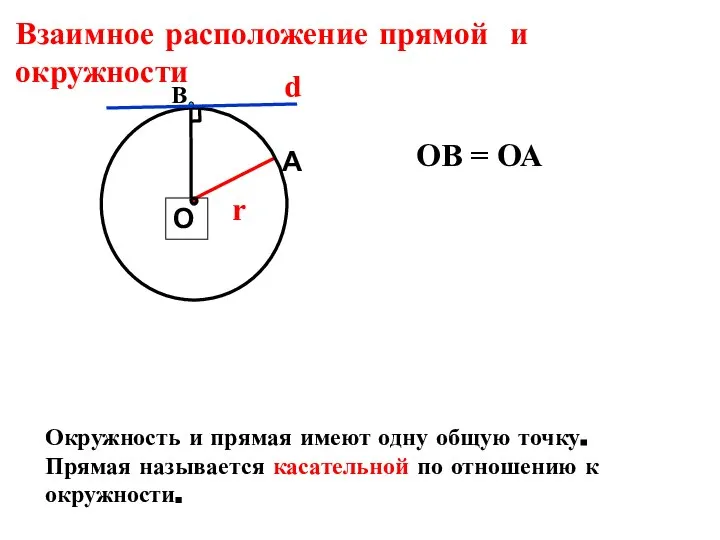
Взаимное расположение прямой и окружности
В
r
ОВ = ОА
Окружность и прямая имеют одну общую точку.
Прямая называется касательной по отношению к окружности.
А
d

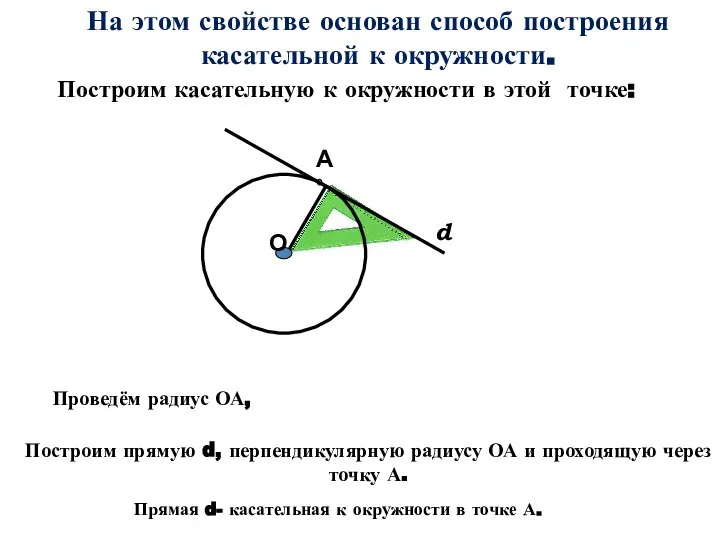
А
О
d
На этом свойстве основан способ построения касательной к окружности.
Построим прямую d, перпендикулярную радиусу ОА и проходящую через точку А.
Построим касательную к окружности в этой точке:
Проведём радиус ОА,
Прямая d- касательная к окружности в точке А.

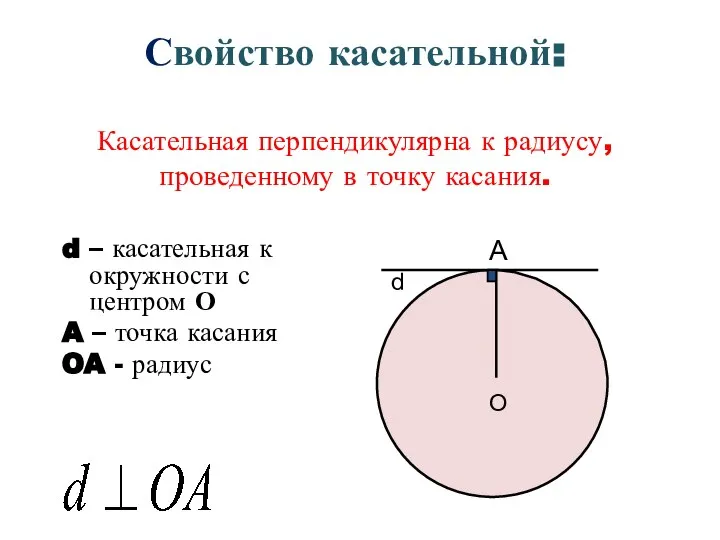
Свойство касательной:
Касательная перпендикулярна к радиусу, проведенному в точку касания.
d – касательная к окружности с центром О
A – точка касания
OA - радиус
O
A
d

Решение задач

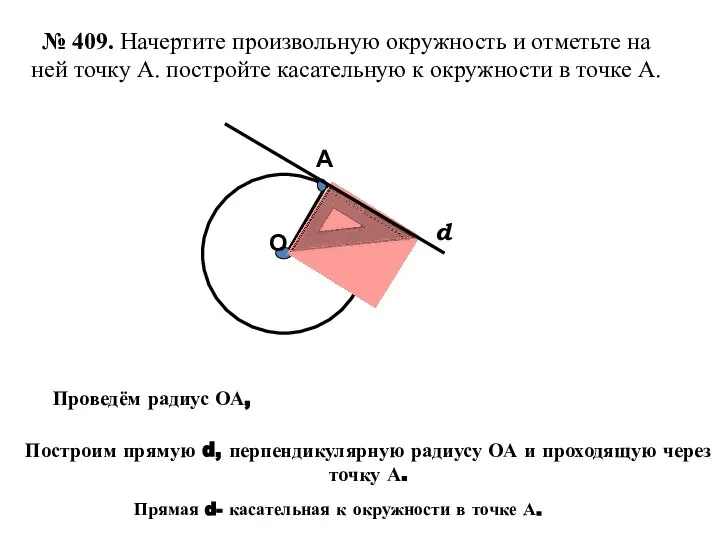
А
О
d
Построим прямую d, перпендикулярную радиусу ОА и проходящую через точку А.
№ 409. Начертите произвольную окружность и отметьте на ней точку А. постройте касательную к окружности в точке А.
Проведём радиус ОА,
Прямая d- касательная к окружности в точке А.

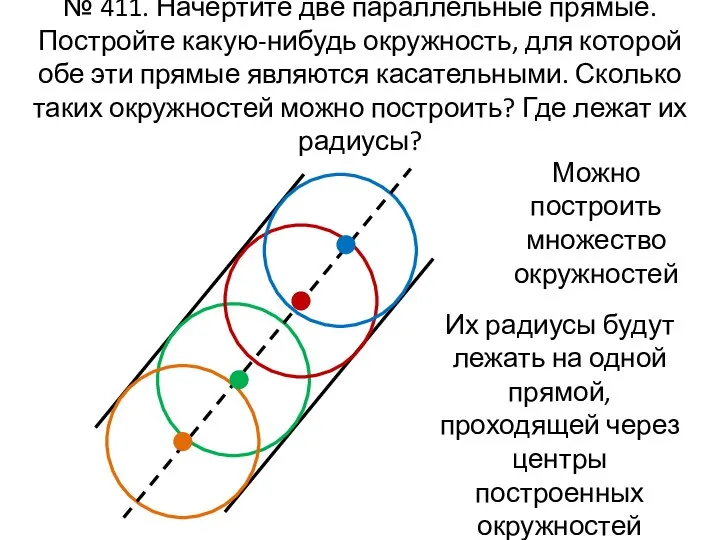
№ 411. Начертите две параллельные прямые. Постройте какую-нибудь окружность, для которой обе эти прямые являются касательными. Сколько таких окружностей можно построить? Где лежат их радиусы?
Можно построить множество окружностей
Их радиусы будут лежать на одной прямой, проходящей через центры построенных окружностей

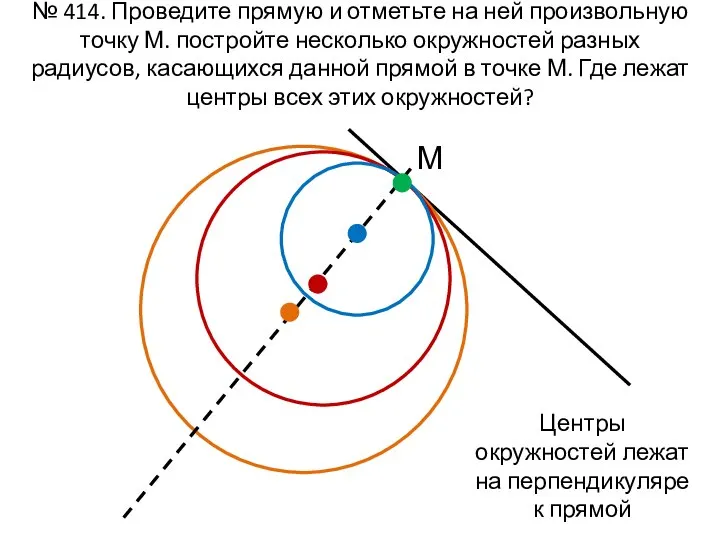
№ 414. Проведите прямую и отметьте на ней произвольную точку М. постройте несколько окружностей разных радиусов, касающихся данной прямой в точке М. Где лежат центры всех этих окружностей?
М
Центры окружностей лежат на перпендикуляре к прямой