Содержание
- 2. Решение По правилу треугольников три положительных члена определителя представляют собой произведение элементов главной диагонали и элементов,
- 3. Решение Найдём три положительных члена определителя. По правилу Сарруса первое слагаемое будет представлять произведение элементов главной
- 4. Решение Второе и третье слагаемые представляют собой произведения элементов, находящихся в вершинах двух равнобедренных треугольников, основания
- 5. Решение Второе и третье слагаемые представляют собой произведения элементов, находящихся в вершинах двух равнобедренных треугольников, основания
- 6. Решение Найдём три отрицательных члена определителя. По правилу Сарруса они состоят из произведения элементов побочной диагонали
- 7. Решение и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали: 3·1·(-2) +
- 8. Решение и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали: 3·1·(-2) +
- 10. Скачать презентацию







 Геометрия в жизни человека
Геометрия в жизни человека Действия с десятичными дробями
Действия с десятичными дробями Оператор Лапласа в полярных, цилиндрических и сферических системах координат
Оператор Лапласа в полярных, цилиндрических и сферических системах координат Решение задач. Линейные динамические системы
Решение задач. Линейные динамические системы Логарифмические уравнения
Логарифмические уравнения Статистическое наблюдение
Статистическое наблюдение Презентация на тему Параллелепипед и его объем
Презентация на тему Параллелепипед и его объем  Презентация на тему ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
Презентация на тему ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ  Презентация на тему Задачи по теме треугольники
Презентация на тему Задачи по теме треугольники  Баскетбол. Математическая викторина
Баскетбол. Математическая викторина Первое знакомство с понятием вероятность. Урок 145
Первое знакомство с понятием вероятность. Урок 145 Измерительные работы
Измерительные работы Правильные многогранники
Правильные многогранники Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач
Рассчитать площадь и периметр прямоугольника по двум известным сторонам. Алгоритм решения подобных задач Шаг в науку. Мир фракталов
Шаг в науку. Мир фракталов Презентация на тему Логарифмическая функция в уравнениях
Презентация на тему Логарифмическая функция в уравнениях  Презентация на тему Параллельность прямых и плоскостей (10 класс)
Презентация на тему Параллельность прямых и плоскостей (10 класс)  Основы тригонометрии. Упражнения
Основы тригонометрии. Упражнения Геометрия Евклида
Геометрия Евклида Дроби, проценты, пропорции в задачах с экономическим содержанием
Дроби, проценты, пропорции в задачах с экономическим содержанием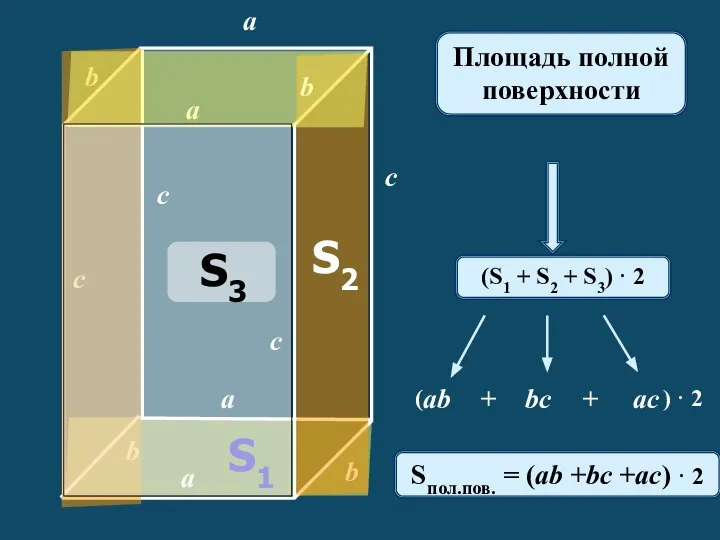 Площадь полной поверхности
Площадь полной поверхности Статистмческие методы
Статистмческие методы Решение линейных уравнений. Часть 2
Решение линейных уравнений. Часть 2 формулы нахождения периметра прямоугольника, периметра квадрата
формулы нахождения периметра прямоугольника, периметра квадрата Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Формула Ньютона-Лейбница. Площадь криволинейной трапеции Радианная мера угла. Синус, косинус, тангенс числа
Радианная мера угла. Синус, косинус, тангенс числа Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ