Содержание
- 2. таңбасымен белгіленген, кез келген сандар кестесіне белгілі бір заңдылықпен сәйкес қойылатын қандай да бір сан n-ші
- 3. Анықтауыштың элементінің миноры арқылы белгіленеді n-ші ретті анықтауыштың aij элементінің миноры Мij деп осы элемент тұрған
- 4. Анықтауыштың алгебралық толықтауышы деп осы элементтің (-1)i+j көбейтілген минорын айтамыз, мұндағы i - элементтің орналасқан жолы
- 5. Алгебралық толықтауышы:
- 6. Мысалы: Миноры Алгебралық толықтауышы aij называется число – минор элемента а23. A23=(-1)2+3 М23=(-1)(-6)=6.
- 7. Лаплас формуласы:
- 8. Лаплас формуласын қолданып, анықтауышты 3-ші жолының элементтері бойынша жіктейік: ⎜A⎜ =a31A31+a32A32+a33A33,
- 9. Анықтауыштардың қасиеттері. 1 o . Анықтауышты транспонерлегеннен анықтауыштың мәні өзгермейді, яғни |A|=|A T |. 2 o
- 10. 5 o . Анықтауыштың кез келген екі жолының (бағанының) сәйкес элементтері өзара тең немесе прапорционал болса,
- 11. 7 o . Анықтауыштың кез келген бір жолының (бағанының) элементтерін бірдей санға көбейтіп, басқа жолдың (бағанның)
- 12. 8 o . Кез келген жолдың (бағанның) элементтері мен, сол элементтерге сәйкес алгебралық толықтауыштарының көбейтінділерінің қосындысы
- 13. Екінші және үшінші ретті анықтауыштар дегеніміз не? Анықтауыштың қандай қасиеттері бар? Анықтауыштың миноры дегеніміз не? Алгебралық
- 15. Скачать презентацию












 Площадь боковой поверхности тела вращения. Лекция №11
Площадь боковой поверхности тела вращения. Лекция №11 Цепочки. Сравните выражения
Цепочки. Сравните выражения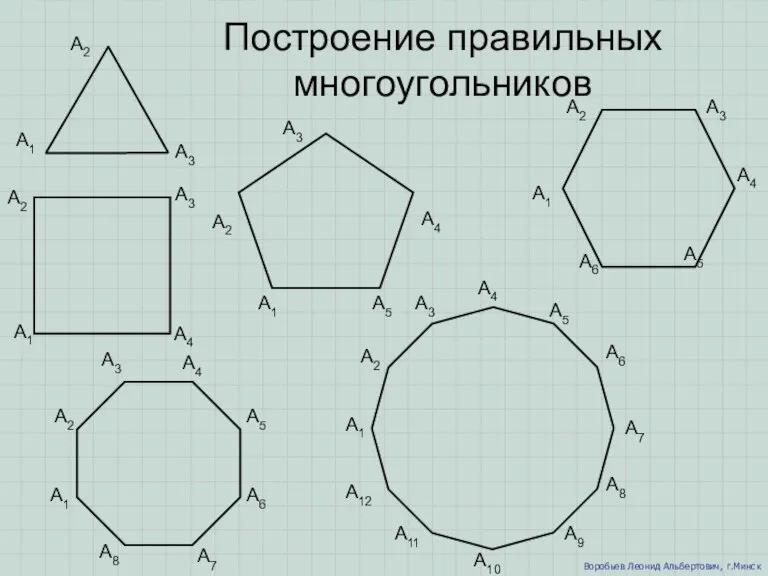 Построение правильных многоугольников
Построение правильных многоугольников Комплексные числа и квадратные уравнения
Комплексные числа и квадратные уравнения Найди фигуру (развиваем логику)
Найди фигуру (развиваем логику) Закрепление знаний. Страничка для любознательных
Закрепление знаний. Страничка для любознательных Эквивалентные бесконечно малые функции
Эквивалентные бесконечно малые функции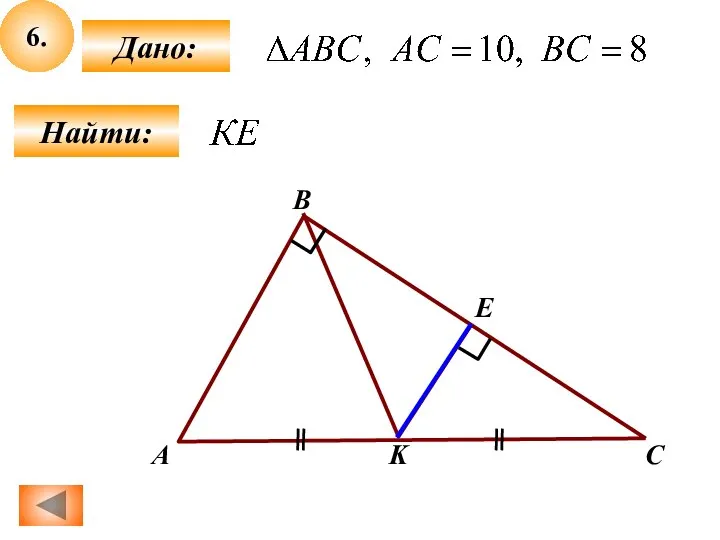 Задачи по геометрии (6-7)
Задачи по геометрии (6-7) Презентация на тему Деление десятичных дробей
Презентация на тему Деление десятичных дробей  Проценты
Проценты Экстремумы функции
Экстремумы функции История зарождения и развития геометрии
История зарождения и развития геометрии Число 8
Число 8 Чтение графика функции
Чтение графика функции Степень с рациональным показателем. Множество рациональных чисел
Степень с рациональным показателем. Множество рациональных чисел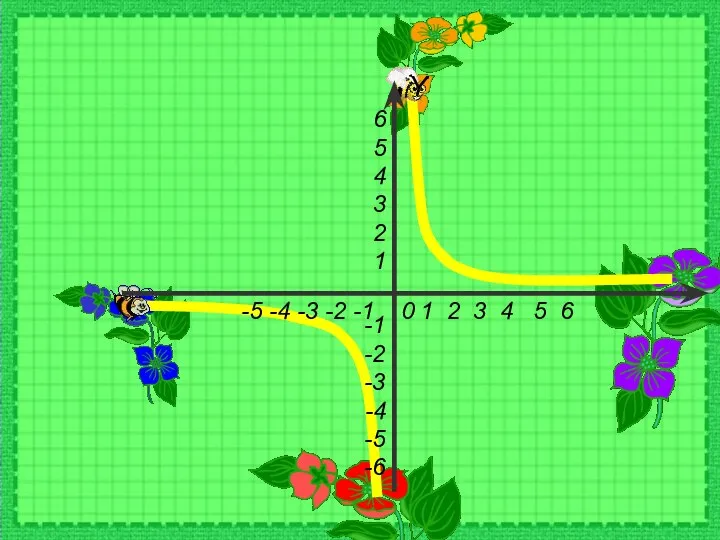 Функция у=1/х и её график
Функция у=1/х и её график Математические основы криптографии
Математические основы криптографии 6a04a5dd-75c3-461b-a240-737df2a5d137
6a04a5dd-75c3-461b-a240-737df2a5d137 Алгебра логики
Алгебра логики Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого Комбинаторные задачи. 9 класс
Комбинаторные задачи. 9 класс Решение задач на оптимизацию методами математического анализа
Решение задач на оптимизацию методами математического анализа Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Графическое и табличное представление информации
Графическое и табличное представление информации Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Сложение чисел. Тренажер, 1 класс
Сложение чисел. Тренажер, 1 класс