Содержание
- 2. Актуальность темы обусловлена тем, что интеллектуальные игры развивают способности, необходимые для решения инженерных задач, проблем управления
- 3. Некоторые математические игры появились еще в древности. Создавали такие игры еще древнегреческие математики и египтяне. Из
- 4. Изображение игры сенет на стене (Египет)
- 5. История игры «Го» Известная в настоящее время игра «Го» возникла в Китае. Китайские легенды приписывают ей
- 6. Игра « Го» классическая игра на логику и умение стратегически мыслить . Чтобы одолеть соперника вам
- 7. Виды игровых задач по способам решений: Игры-шутки. Игры, использующие симметрию. Игры, в которых стратегия — дополнение
- 8. Игры - шутки Это игры, исход которых не зависит от того, как играют соперники. Поэтому для
- 9. Пример игры-шутки: Двое по очереди ломают шоколадку 6x8. За ход можно разломать любой кусок по прямой
- 10. Решение После каждого хода число кусков шоколадки увеличивается на единицу. Ломая шоколадку 6x8, мы из одного
- 11. Решение задачи в общем виде Если число кусочков шоколадки четно, тогда побеждает первый, если число нечетно,
- 12. Игры, использующие симметрию Суть метода - делать каждый раз ход, симметричный ходу противника или дополняющий его
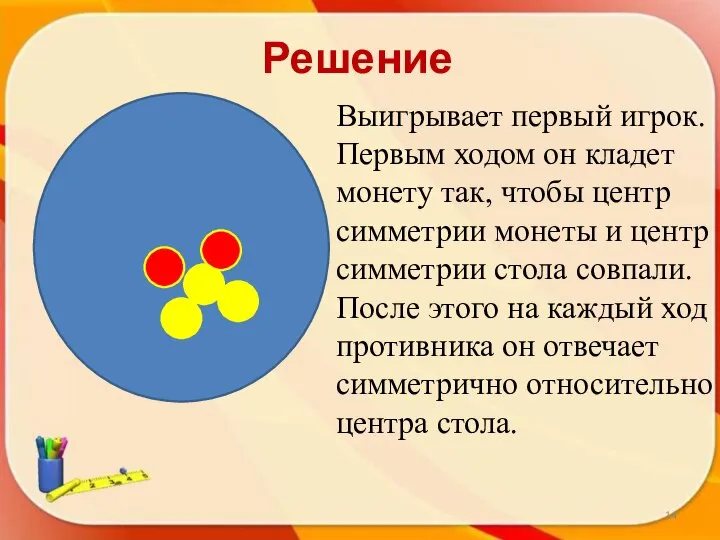
- 13. Пример игры на симметрию: Двое по очереди кладут пятаки на круглый стол так, чтобы они не
- 14. Решение Выигрывает первый игрок. Первым ходом он кладет монету так, чтобы центр симметрии монеты и центр
- 15. Дополнение до фиксированного числа Выигрышная стратегия – дополнение хода соперника до некоторого фиксированного числа, уменьшая каждым
- 16. Дополнение до фиксированного числа Из кучи камней двое играющих по очереди берут 1, 2, 3 или
- 17. Поиск выигрышных позиций Суть метода: делим всю доску (или всевозможные ходы) на два вида полей –
- 18. Проводя свободные часы за шахматной доской, за поединком в «Го» или шашки, играя в слова или
- 19. Гипотеза, что математические игры актуальны в современном мире, доказана. Одних только шахматных и шашечных книг в
- 21. Скачать презентацию

















 Тренажёр по математике Морское приключение
Тренажёр по математике Морское приключение Построение сечений
Построение сечений Ромб: признаки и свойства
Ромб: признаки и свойства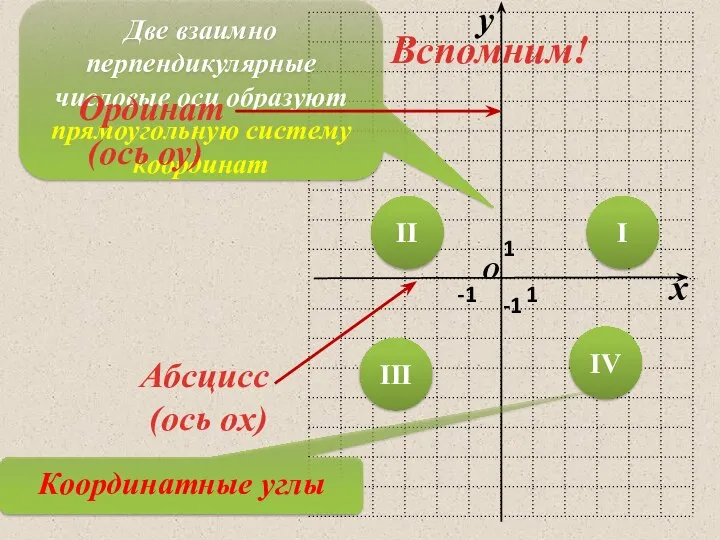 Прямоугольная система координат
Прямоугольная система координат Решение уравнений: рациональных и иррациональных
Решение уравнений: рациональных и иррациональных Презентация на тему ТРАПЕЦИЯ. ПЛОЩАДЬ ТРАПЕЦИИ
Презентация на тему ТРАПЕЦИЯ. ПЛОЩАДЬ ТРАПЕЦИИ  Связь между компонентами и результатом умножения. Чётные и нечётные числа
Связь между компонентами и результатом умножения. Чётные и нечётные числа Усечённый конус
Усечённый конус Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж
Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж Категориальные переменные
Категориальные переменные Двухфакторный дисперсионный анализ
Двухфакторный дисперсионный анализ Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)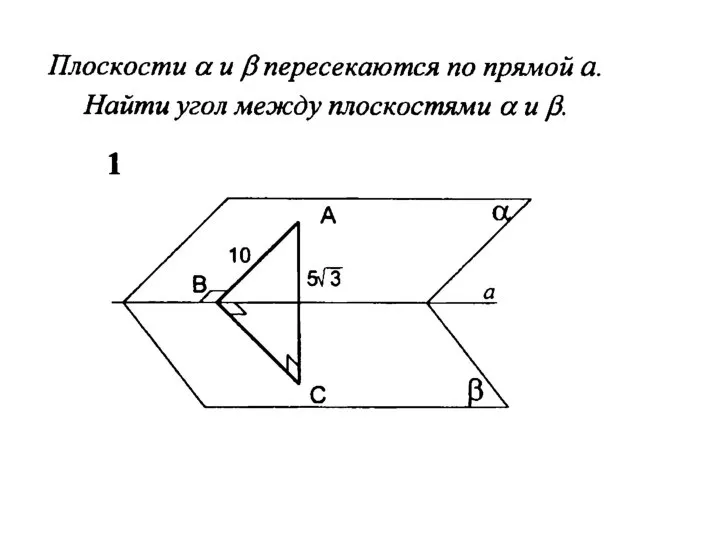 Угол между плоскостями
Угол между плоскостями Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Понятие квадратного уравнения
Понятие квадратного уравнения Округление чисел
Округление чисел Решение задач на проценты
Решение задач на проценты Письменное умножение трехзначных чисел (3 класс)
Письменное умножение трехзначных чисел (3 класс) Перпендикулярные прямые
Перпендикулярные прямые Эквивалентные преобразования формул
Эквивалентные преобразования формул Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Сложение отрицательных чисел. 6 класс
Сложение отрицательных чисел. 6 класс Комплексные числа
Комплексные числа Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница
Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница Презентация на тему Система координат в пространстве
Презентация на тему Система координат в пространстве  Средняя линия треугольника
Средняя линия треугольника Палички Непера
Палички Непера Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента