Слайд 2Центральная симметрия
Движение пространства – это отображение пространства на себя, при котором любые
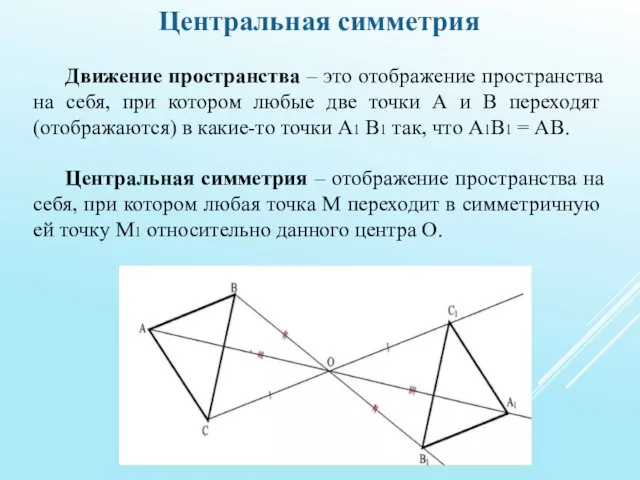
две точки А и В переходят (отображаются) в какие-то точки А1 В1 так, что А1В1 = АВ.
Центральная симметрия – отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.
Слайд 3Центральная симметрия
В случае центральной симметрии относительно начала координат все координаты точки меняют

знак на противоположный. Рассмотрим несколько примеров:
А (-8; 5; 27) → А1 (8; -5; -27)
В (4; 0; -9) → В1 (-4; 0; 9)
С (2; -15; 0) → С1 (-2; 15; 0)
Слайд 4Осевая симметрия
Осевая симметрия – такое отображение пространства на себя, при котором любая
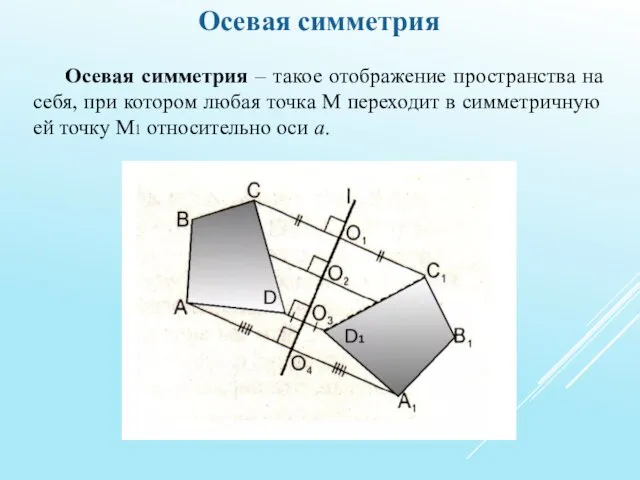
точка М переходит в симметричную ей точку М1 относительно оси а.
Слайд 5Осевая симметрия
В случае осевой симметрии относительно координатной оси, все координаты, кроме той,

которая соответствует данной оси, меняют свой знак на противоположный. Рассмотрим несколько примеров:
1) для оси Ох:
А (-8; 5; 27) → А1 (-8; -5; -27)
В (4; 0; -9) → В1 (4; 0; 9)
С (2; -15; 0) → С1 (2; 15; 0)
2) для оси Оу:
А (-8; 5; 27) → А1 (8; 5; -27)
В (4; 0; -9) → В1 (-4; 0; 9)
С (2; -15; 0) → С1 (-2; -15; 0)
3) для оси Оz:
А (-8; 5; 27) → А1 (8; -5; 27)
В (4; 0; -9) → В1 (-4; 0; -9)
С (2; -15; 0) → С1 (-2; 15; 0)
Слайд 6Зеркальная симметрия
Зеркальная симметрия (симметрия относительно плоскости α) – такое отображение пространства на
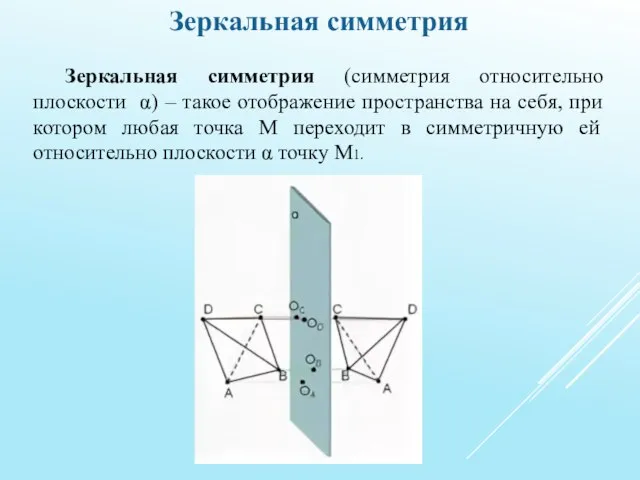
себя, при котором любая точка М переходит в симметричную ей относительно плоскости α точку М1.
Слайд 7Зеркальная симметрия
В случае зеркальной симметрии относительно координатной плоскости, меняется только та координата,

которая не принадлежит данной плоскости. Рассмотрим несколько примеров:
1) для плоскости хОу:
А (-8; 5; 27) → А1 (-8; 5; -27)
В (4; 0; -9) → В1 (4; 0; 9)
С (2; -15; 0) → С1 (2; -15; 0)
2) для плоскости уОz:
А (-8; 5; 27) → А1 (8; 5; 27)
В (4; 0; -9) → В1 (-4; 0; -9)
С (2; -15; 0) → С1 (-2; -15; 0)
3) для плоскости хОz:
А (-8; 5; 27) → А1 (-8; -5; 27)
В (4; 0; -9) → В1 (4; 0; -9)
С (2; -15; 0) → С1 (2; 15; 0)






 Строение функции, свойства, графики
Строение функции, свойства, графики Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Проверка умножения делением
Проверка умножения делением Монотонность функции
Монотонность функции Таблица умножения в пределах 100. Урок повторения и закрепления
Таблица умножения в пределах 100. Урок повторения и закрепления Волшебный мир иллюзий
Волшебный мир иллюзий Презентация на тему Слагаемые Сумма
Презентация на тему Слагаемые Сумма  Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем ГИА - 2016. Открытый банк заданий по математике. Задача №15
ГИА - 2016. Открытый банк заданий по математике. Задача №15 Презентация на тему Квадратный сантиметр (3 класс)
Презентация на тему Квадратный сантиметр (3 класс) 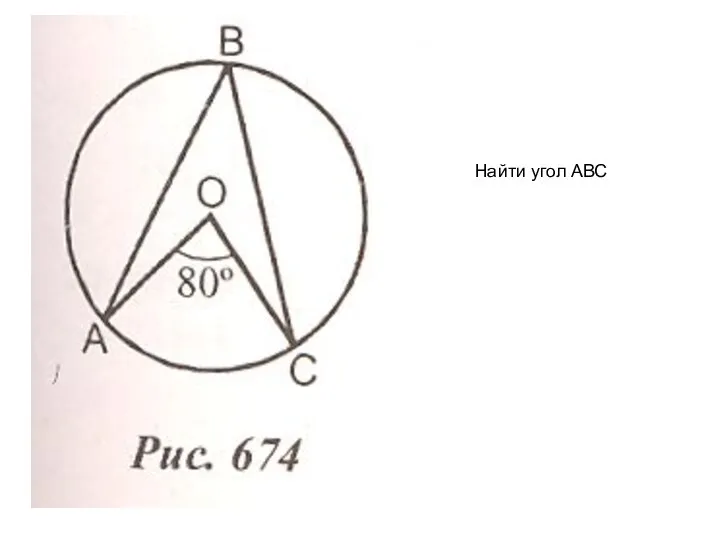 Найти угол АВС
Найти угол АВС Элементы комбинаторики
Элементы комбинаторики Практикум по решению комбинированных уравнений
Практикум по решению комбинированных уравнений Пирамида. Построение правильной треугольной пирамиды
Пирамида. Построение правильной треугольной пирамиды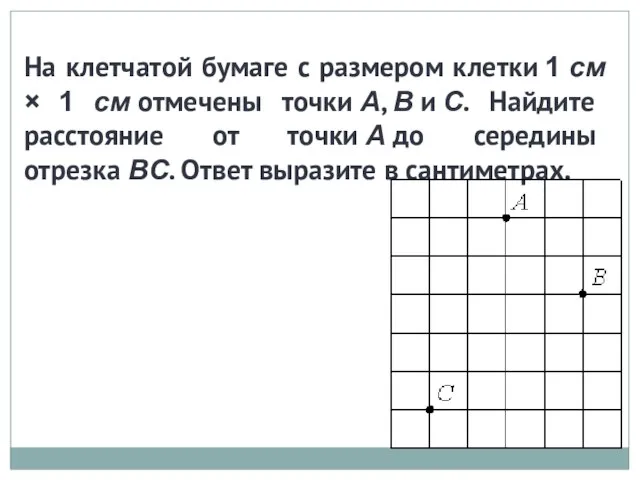 Решение задач
Решение задач МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид
МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете Белоусова Алла Генриховна, учитель математики, кандид Треугольники. Задача
Треугольники. Задача Приложения скалярного произведения
Приложения скалярного произведения Планы второго порядка
Планы второго порядка Параллелограмм и трапеция
Параллелограмм и трапеция Математика звука
Математика звука Elemente de teoria reziduurilor
Elemente de teoria reziduurilor Многогранники. Тела Архимеда
Многогранники. Тела Архимеда Системы уравнений. Основные понятия
Системы уравнений. Основные понятия Презентация на тему Прибавление и вычитание числа 3
Презентация на тему Прибавление и вычитание числа 3  Решение задач
Решение задач Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі
Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний