Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи

«В математике есть своя красота, как в живописи и поэзии»
Н.Е. Жуковский

1. В одном элеваторе было зерна в два раза больше, чем в другом. Из первого элеватора вывезли 750 т зерна, во второй элеватор привезли 350 т, после чего в обоих элеваторах зерна стало поровну. Сколько зерна было первоначально в каждом элеваторе?
Пусть AK = CE = x, тогда, так как AB = 2CD, получим
x + 750 = 2(x – 350),
откуда x = 1450, CD = 1450 – 350 = 1100, AB = 1100·2 = 2200.
2. Пусть CD = x, тогда AB = 2x.
Так как AK = CE, то имеем 2x – 750 = x + 350

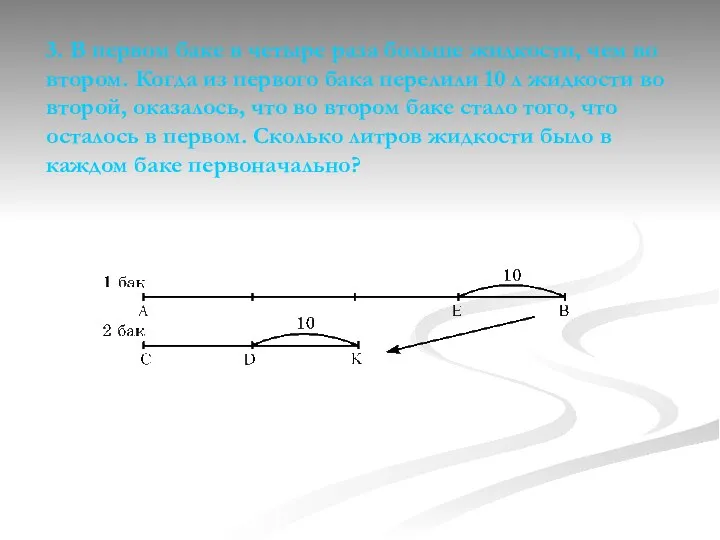
2. На одном садовом участке в пять раз больше кустов малины, чем на другом. После того как с первого участка пересадили на второй 22 куста, то на обоих участках кустов малины стало поровну. Сколько кустов малины было на каждом участке?
AB и 5CD — первоначальное распределение кустов малины между участками.
Так как на обоих участках кустов малины стало поровну, то разделим отрезок BE пополам (BF = FE) и из отрезка AB вычтем отрезок BF, а к отрезку CD прибавим отрезок DK (DK = BF). AF = CK — конечное распределение кустов малины между участками.
По условию с первого участка пересадили на второй 22 куста, значит,
BF = 22 = 2CD, тогда CD = 11, AB = 5CD = 5·11 = 55.

3. В первом баке в четыре раза больше жидкости, чем во втором. Когда из первого бака перелили 10 л жидкости во второй, оказалось, что во втором баке стало того, что осталось в первом. Сколько литров жидкости было в каждом баке первоначально?

4. Бригада лесорубов ежедневно перевыполняла норму на 16 м3, поэтому недельную норму (шесть рабочих дней) она выполнила за четыре дня. Сколько кубометров леса заготовляла бригада в день?
Пусть SABCD определяет недельную норму бригады лесорубов. AB — производительность (м3) бригады в день по плану; AD — количество дней; SAMNK — объем работы, выполненный бригадой за четыре дня.
SAMNK = SABCD = S;
S1 = S2, так как S1 + S3 = S2 + S3.
S1 = 2KE, S2 = 16·4 = 64,
значит 2KE = 64, тогда KE = 32.
AB = KE = 32, AM = AB + BM = 32 + 16 = 48.
Если АВ=Х , то получаем 6Х=4(Х +16).

Найдите значение выражения tg ( arcSin )
По определению арксинуса имеем
, причем, если ,
то .
Поэтому
и

Вычислить
В
А
С
Решение:
где острый угол прямоуг. равнобед.
АВ2 = АС2+ ВС2,(по т., обратной т. Пифагора)
Следовательно, , а
, тогда
Таким образом,

Выразить острый угол, равный
через все остальные arc функции.
Решение:
А
В
С
7
1
-острый угол прям. треуг.,
в котором противолежащий ему катет
a=7, а гипотенуза с= . По т.Пифагора
катет в = . Тогда искомый угол
будет или
или .

Желаем всем счастья
от минус до плюс бесконечности.
Чтобы ваши
удачи и победы приумножались,
а неудачи и поражения делились.